Курсовая работа
по дисциплине: «Теория связи»
КР 23.05.05.631
Выполнил: Королёв А.И.
Группа: 631
Проверил: Стафеев А.В
Хабаровск, 2019
ВВЕДЕНИЕ
В данной курсовой работе рассчитываются:
1. Источник сообщений. Раздел «Расчёт информационных параметров сообщения».
2. Кодер источника. Раздел «Статистическое кодирование сообщения».
3. Кодер канала. Раздел «Помехоустойчивое кодирование сообщения».
4. Преобразователи сообщения в сигнал и сигнала в сообщение. Раздел «Модуляция и демодуляция сигналов». Здесь же производится расчёт помехоустойчивости системы передачи сигналов.
Оглавление
ВВЕДЕНИЕ. 2
1.Расчет информационных параметров сообщения. 4
Задание 1.1. 4
2.СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ СООБЩЕНИЯ. 5
Заданик 2.1. 5
3.ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЯ. 7
Задание 3.1. 7
4.МОДУЛЯЦИЯ И ДЕМОДУЛЯЦИЯ СИГНАЛОВ. 11
Задание 4.1. 11
Задание 4.2. 13
ЗАКЛЮЧЕНИЕ. 16
Расчет информационных параметров сообщения.
Задание 1.1
Определить энтропию,количество информации и избыточность сообщения состоящего из букв Фамилии Имени Отчество студента.
Решение задания 1.1
Сообщение «Королёв Артём Игоревич».
Длина сообщения:n=8+7+9=23 буквы.
Алфавит, используемый в сообщении:
α∈{Ч,е,р,н,а,в,и,,Д,с,л,о }
Количество букв: m=11 букв.
Частота появления букв в сообщении:
«ч» - встречается 2 раза, n(ч)=2;
«е» - встречается 3 раза,n(е)=3;
«р» - встречается 1 раз,n(р)=1;
«н» - встречается 4 раза,n(н)=4;
«а» - встречается 1 раз,n(а)=1;
«в» - встречается 2 раза,n(в)=2;
«и» - встречается 4 раза,n(и)=4;
«д» - встречается 2 раза,n(д)=2;
«с» - встречается 1 раз,n(с)=1;
«л» - встречается 1 раз,n(л)=1;
«о» - встречается 2 раза,n(о)=2;
Находим вероятности появления букв:
p(р)=p(а)=p(с)=p(л)= 1/23;
p(ч)=p(в)= p(д)= p(0)=2/23;
p(е)=3/23;
p(н)= p(и)= 4/23;
Проверяем правильность расчета по формуле полной вероятности:
6p(л)+2p(в)+ p(д) +p(а)+p(е)=1;
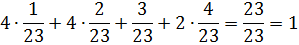
Находим максимальную энтропию по формуле:
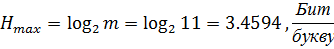
Теперь находим энтропию по формуле (символы неравновероятны):
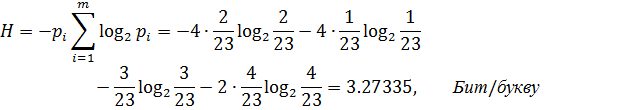
Далее находим избыточность:
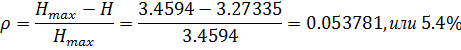
Считаем количество информации в сообщении:
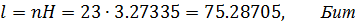
СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ СООБЩЕНИЯ
Заданик 2.1
Произвести статистическое кодирование буквенного сообщения, со-стоящие из Фамилии Имени Отчества студента.
Для чётного числа единиц в первых двух буквах фамилии студента – методом Шеннона-Фано, для нечётного числа единиц в первых двух буквах фамилии студента – мето-дом Хаффмана.
Показать, что полученный код является префиксным. Вычислить остаточную избыточность.
Воспользоваться вычисленными вероятностями букв из предыду-щего задания.
Решение задния 2.1
Сообщение «Чернавин Денис Леонидович».
«Ч» - 0100 0010 0111; «е» - 0100 0011 0101. Первые две буквы фамилии студента имеют десять единиц, чётное число. Поэтому производим статистическое кодирование, согласно заданию, методом Шеннона-Фано. Разместим буквы в таблице 2.3, в порядке убывания вероятности и произведём кодирование. Пробелы между словами можно не учитывать. Буквы с одинаковой вероятностью размещаем произвольно.
Представим фамилию в двоичном виде (таблица 1):
Таблица 1
| Буква ai | Вер-ть | Элементы кодовых комбинаци | Код. комб | Длина символа ai | |||||||
| и | 4/23 | ||||||||||
| н | 4/23 | ||||||||||
| е | 3/23 | ||||||||||
| в | 2/23 | ||||||||||
| д | 2/23 | ||||||||||
| о | 2/23 | ||||||||||
| ч | 2/23 | ||||||||||
| а | 2/23 | ||||||||||
| л | 1/23 | ||||||||||
| р | 1/23 | ||||||||||
| с | 1/23 |
H=3.27335 Бит/букву.
Hmax=log2(11)=3.4595 Бит/букву.
P=5.4%
Средняя длина одной буквы после кодирования:
 Бит/букву.
Бит/букву.
Кодирование является оптимальным, если выполняется соотношение: Lср= H.
Избыточность после кодирования:
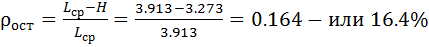 .
.
Общая длина сообщения после кодирования:
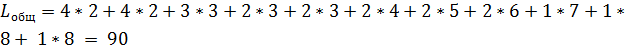 Бит.
Бит.
Данный код является префиксным, т.к. короткая кодовая комбинация не является началом более длинной(таблица 1).
ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЯ
Задание 3.1
Произвести помехоустойчивое кодирование циклическим кодом двоичного сообщения, состоящего из третьей буквы фамилии студента (без четырёх нулей в начале). Определить синдромы для всех вариантов одиночных ошибок.
Выполнения задания 3.1:
Фамилия - Чернавин. Третья буква фамилии – «р».
Записываем в двоичном виде, «р» - 0х0440 – 0000 0100 0100 0000. Без четырёх первых нулей: 0100 01000 0000.
Математическая запись:
𝐾(𝑥) = 0 ∙ 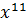 + 1 ∙
+ 1 ∙ 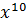 + 0 ∙
+ 0 ∙ 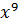 + 0 ∙
+ 0 ∙ 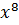 + 0 ∙
+ 0 ∙ 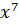 + 1 ∙
+ 1 ∙ 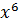 + 0 ∙
+ 0 ∙ 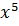 + 0 ∙
+ 0 ∙ 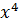 +
+
+ 0 ∙ 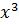 3 + 0 ∙
3 + 0 ∙ 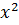 + 0 ∙
+ 0 ∙ 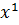 + 0 ∙
+ 0 ∙ 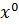
𝐾(𝑥) = 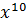 +
+ 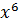 .
.
k=11 - колличество информационных символов
Рассчитываем колличество проверочных символов - r:
𝑟 =⌈ 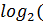 k + 1)⌉ = ⌈
k + 1)⌉ = ⌈ 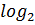 (11 + 1)⌉ = ⌈3,585⌉ = 4
(11 + 1)⌉ = ⌈3,585⌉ = 4
Выбираем порождающий полином четвёртой степени:
G(x)= 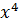 +x+1.
+x+1.
Умножаем K(x) на 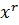 :
:
𝐾(𝑥) ∙ 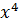 =
= 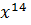 +
+ 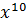
Для нахождения остатка R(x) производим деление:
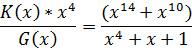
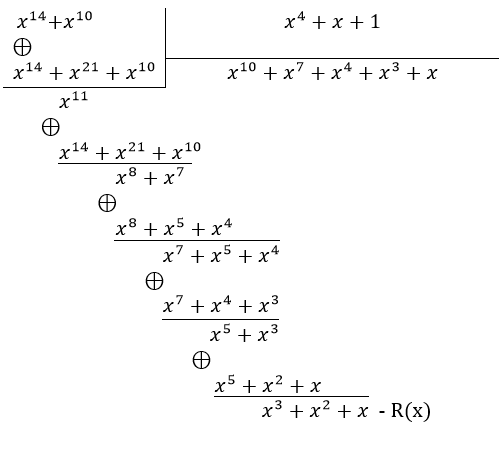
Кодовая комбинация будет иметь вид:
𝑁(𝑥) = 𝐾(𝑥) ∙ 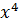 + 𝑅(𝑥) =
+ 𝑅(𝑥) = 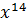 +
+ 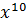 +
+ 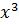 +
+ 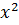 + x
+ x
В двоичном виде: 100 0100 0000 1110. Четыре последних разряда являются проверочными.
Таблица 2
| Разряд с ошибкой | Вектор ошибки | Принятая кодовая комбинация N”(x) | Остаток от деления N”(x)/G(x) (синдром ошибки | Синдром ошибки в двоичном виде |
| Ошибки нет | 000 0000 0000 0000 | 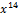 + + 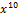 + +  + +  + x + x
| ||
| 000 0000 0000 0001 | 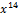 + + 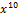 + +  + +  + + 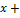 1 1
| |||
| 000 0000 0000 0010 | 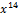 + + 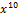 + +  + + 
| x | ||
| 000 0000 0000 0100 | 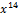 + + 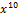 + +  + x + x
| 
| ||
| 000 0000 0000 1000 | 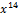 + + 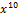 + +  + +  + x + x
| 
| ||
| 000 0000 0001 0000 | 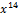 + + 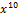 + + 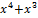 + +  + x + x
| x+1 | ||
| 000 0000 0010 0000 | 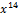 + + 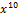 + + 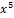 + +  + +  + x + x
|  +x +x
| ||
| 000 0000 0100 0000 | 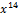 + + 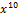 + + 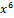 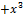 + +  + x + x
|  + + 
| ||
| 000 0000 1000 0000 | 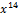 + + 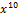 + + 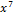 + +  + +  + x + x
|  +x+1 +x+1
| ||
| 000 0001 0000 0000 | 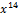 + + 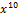 + + 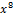  + +  + x + x
|  +1 +1
| ||
| 000 0010 0000 0000 | 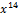 + + 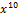 + + 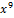 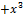 + +  + x + x
|  +x +x
| ||
| 000 0100 0000 0000 | 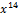 + +  + +  + x + x
|  +x+1 +x+1
| ||
| 000 1000 0000 0000 | 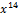 + + 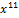 + + 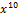 + +  + +  + x + x
|  + +  +x+ +x+
| ||
| 001 0000 0000 0000 | 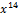 + + 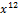 + + 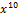 + +  + +  + x + x
|  + +  +x+1 +x+1
| ||
| 010 0000 0000 0000 | 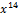 + + 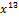 + + 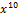 + +  + +  + x + x
|  + +  +1 +1
| ||
| 100 0000 0000 0000 | 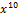 + +  + +  + x + x
|  +1 +1
|
Таким образом, каждому вектору ошибки соответствует свой синдром. Поэтому, зная синдром, можно определить в каком разряде принятой кодовой комбинации произошла ошибка и исправить её.