По определению длительности замораживания
Пищевых продуктов
Цель работы
Познакомиться с расчетными методиками определения длительности замораживания пищевых продуктов. Оценить точность методик путем сравнения расчетных и экспериментальных данных.
Задание
1. Для заданных продуктов и условий рассчитать длительность замораживания по двум расчетным методикам.
2. Экспериментально проверить полученные результаты.
3. Рассчитать относительную погрешность точности используемых расчетных методик путем сравнения расчетных и экспериментальных данных.
Оборудование
1. Стенд холодильный.
2. Секундомер.
Общие сведения
Замораживанием называется такая технология холодильной обработки, при которой среднеобъемная температура продукта на 10…30 0С ниже его криоскопической, а количество вымороженной влаги составляет не менее 70 %. Процесс замораживания продуктов питания – сложный многофакторный процесс, длительность которого зависит от размеров и формы продукта, особенности его структуры, распределения в нем влаги и т.д. Поэтому с целью упрощения математического описания при расчете длительности замораживания используют различные допущения и математические упрощения, позволяющие оценить длительность процесса с допустимой для технических условий долей вероятности. К таким допущениям относят:
– постоянство температуры замерзания;
– принятие удельной теплоты замораживания равной теплоте льдообразования;
– коэффициент теплопроводности замороженного продукта считают постоянным, а его теплоемкость равной нулю;
– коэффициент поверхностной теплоотдачи продукта и температура теплоотводящей среды принимаются постоянными.
Для замораживания продукта толщиной dx, м, имеющего площадь поверхности F, м2, отводится тепло dQ,Дж:
dQ=L×r×F×dx,(l)
где L – теплота льдообразования,Дж/кг (данную величину можно принять равной L = 335000 Дж/кг); r –плотность продукта, кг/м3.
Количество тепла, отведенное через замороженный слой толщиной x, применительно к стационарным условиям теплообмена через плоскую стенку для граничных условий III рода можно выразить равенством:
(2)
где tкр – криоскопическая температура продукта, 0C; tc – температура охлаждающей среды, 0C; 
– коэффициент теплопроводности продукта, Вт/м×К (см. табл. П1.3 приложения 1); a – коэффициент теплоотдачи от поверхности продукта к теплоотводящей среде, Вт/м2×К.
Приравнивая правые части формул (1) и (2), можно получить решение относительно длительности замораживания при двустороннем теплоотводе:
(3)
После интегрирования уравнения (3) получаем выражение для определения длительности замораживания продукта, форма которого подобна пластине:
. (4)
Аналогичные решения получены для тел, форма которых подобна цилиндру и шару:
; (5)
. (6)
Выражения (4)…(6) не учитывают того, что продукты перед замораживанием имеют температуру, отличную от криоскопической. Поэтому для практического использования применяют выражения для пластины, цилиндра и шара, в которых теплота льдообразования L заменена теплотой замораживания qз, Дж/кг, которая учитывает теплоту охлаждения и домораживания продукта:
qз = C (tн–tкр) +LWw+Cм (tкр–tск), (7)
где С – теплоемкость продукта до замораживания, Дж/кг×К; tн – начальная температура продукта, 0C; tкр – криоскопическая температура продукта, 0C; L – теплота льдообразования, Дж/кг; W – количество влаги в продуктах, выраженное в долях единицы; w – количество вымороженной воды; См –теплоемкость замороженного продукта, Дж/кг×К; tcк – средняя по толщине температура продукта, 0C.
Тогда выражение (4) применительно к двухстороннему замораживанию бесконечной пластины толщиной d = 2 R преобразуется к виду:
. (8)
To же для цилиндра:
. (9)
Для шара:
, (10)
где lм – коэффициент теплопроводности замороженного продукта, Вт/м×К; R – характерный размер продукта (для пластины – половина толщины, для цилиндра и шара – радиус), м.
Коэффициент теплопроводности замороженного продукта можно определить по выражению:
lм = l+ 1. (11)
Для практических расчетов длительности замораживания продуктов, имеющих конечные размеры, можно использовать выражение:
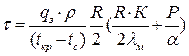, (12)
где К и Р – коэффициенты, зависящие от формы продукта. Они находятся из табл. П1.8 приложения 1 с учетом отношений основных геометрических параметров продуктов:
, (13)
где l и b – длина и ширина продукта соответственно, м.