Лекция13
Частица в прямоугольной потенциальной яме
Решение стационарного уравнения Шрёдингера
Как отмечалось в предыдущей лекции, стационарные состояния частицы определяются потенциальным рельефом, то есть функцией U (x).Для того, чтобы состояния были локализованные, потенциальный рельеф должен быть потенциальной ямой.
В данной лекции мы рассмотрим простейшую потенциальную яму – одномерную и прямоугольную. Она описывается следующим выражением.
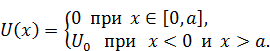
| U (x) |
| x |
| a |
| U 0 |
| E |
| Свободная область 1 |
| Свободная область 2 |
| Яма |
График этой функции показан на рисунке.
Число a мы будем называть шириной ямы, а число U 0– глубиной ямы.Там же на рисунке показан уровень энергии E.
Функция U (x) – кусочно-непрерывная, в точках на границах ямы (x = 0 и x = a) у неё разрывы 1 рода, чего у реальных полей быть не должно. Однако мы можем считать, что кусочно-непрерывная функция U (x) описывает модель реального силового поля, в котором U (x) – строго непрерывна, но она падает от значения U 0до нуля в малой области, окружающей точку x = 0, и нарастает от нуля до U 0в малой области, окружающей точку x = a.
В соответствии с законами классической механики запереть частицу в данной яме можно только при условии, что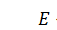 
. В этом случае выход частицы из ямы означает, что 
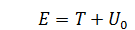, так что кинетическая энергия частицы 
, чего быть не может.
Как мы выяснили в предыдущей лекции, квантовая частица при условии 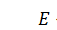тоже оказывается локализованной (связанной), только у области локализации нет точных границ. Это значит, что пси-функция частицы за пределами области локализации становится очень маленькой и очень быстро убывает при удалении от области локализации.
|
|
Для нахождения пси-функции стационарного состояния надо решить стационарное уравнение Шрёдингера (СУШ):
.
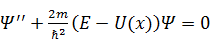Тот факт, что функция U (x) – кусочно-непрерывная, означает, что решение СУШ разное в разных областях пространства. Этих областей три: две из них – это свободные области, они же – классически недоступные:СО-1(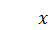
и СО-2 (
), третья область 
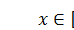– классически доступная, и её естественно называть ямой.
Дляклассически недоступной области СО-2() мы решение СУШ уже нашли в предыдущей лекции:
,
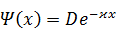где число 
– это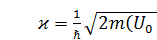 
.
Дляклассически недоступной области СО-1(
) решение СУШ получается аналогично (проделайте самостоятельно):
.
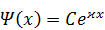Осталось найти пси-функцию в яме, то есть в области 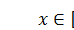. В этой области потенциальная энергия частицы равна нулю, поэтому СУШимеет вид:
.
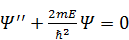Так как энергия частицы положительная, то сомножитель пси-функции в этом уравнении – положительное число. Обозначим его так:
, 
.
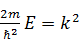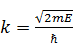В результате получаем стандартное однородноеДУ второго порядка с постоянными коэффициентами, известное как уравнение гармонических колебаний:
.
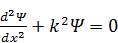Общее решение этого ДУзаписывают в трёх вариантах:
,
,
.
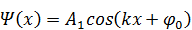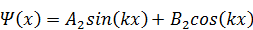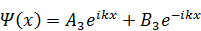Каждый из вариантов решения содержит две произвольные постоянные.
Для того, чтобы увидеть физический смысл решения, удобен третий вариант.
.
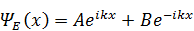Индексы у констант для краткости опущены.
Это – координатная пси-функция, её надо умножить на временной множитель:
.
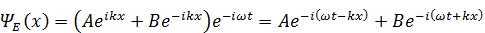Обозначим слагаемые
,
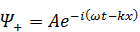
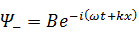так что
,
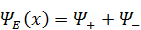и выясним сначала физический смысл первого слагаемого.
.
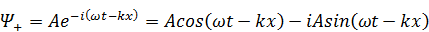Как вещественная, так и мнимая часть функции Ψ + представляют собой уравнения плоской монохроматической волны, распространяющейсяв положительном направлении, то есть в ту сторону, куда направлена ось OX. В этой волне ω – частота колебаний, k – волновое число.
|
|
Аналогично функция Ψ – описывает плоскую монохроматическую волну, распространяющуюся в отрицательном направлении.
Волны Ψ +и Ψ – – когерентные, у них одна и та же частота,одно и то же волновое число, а разность фаз, котораяравна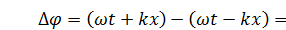 
, не зависит от времени. Поэтому эти волны интерферируют.
Итак, пси-поле частицы в прямоугольной потенциальной яме – это результат интерференции двух встречных плоских волн.
Физическая интерпретация этого факта такова. Сначала в яме по каким-то причинам возникает одна плоская волна – например, Ψ +. Эта волна, налетев на правую границу ямы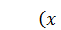 
, отражается от неё, так возникает волна Ψ –,когерентная с волной Ψ +.Волна Ψ – распространяется влево и, налетев на левую границу ямы 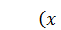, в свою очередь, отражается. При этом новая отражённая волна оказывается точь-в-точь такой же, как и первичная волна Ψ +. Поэтому-то и получается, что в яме присутствуют только две встречные когерентные волны Ψ +и Ψ –, и они, естественно, интерферируют.
Отметим три интересных факта.
Факт первый. Формально введённая величина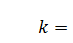 
имеет ясный физический смысл:это – волновое число каждой из двух интерферирующих волн.
Факт второй. Пси-функции Ψ + и Ψ – являются собственными функциями проекции импульса частицы px, то есть описывают состояния частицы с определёнными значениями px. В состоянии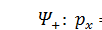 
,в состоянии 
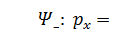. Убедитесь в этом самостоятельно. Физический смысл таков: корпускула, пси-волна которой Ψ +, летит с постоянным импульсом, а значит, с постоянной скоростью туда же, куда распространяется волна Ψ +, то есть в положительном направлении оси OX. А корпускула, пси-волна которой Ψ –, тоже летит с постоянными импульсом и скоростью туда же, куда распространяется волна Ψ –, то есть в отрицательном направлении оси OX.
|
|
Факт третий. Длина волны каждой из волн Ψ + и Ψ – равна
.
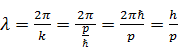Итак, мы получили формулу де Бройля. То, что де Бройль предложил в виде гипотезы, мы получили как естественное следствие законов квантовой механики.
Ещё один полезный результат.Вспомните интересное явление, которое вы изучали в курсе общей физики (раздел «Колебания и волны»): при наложении двух встречных плоских когерентных волн возникает так называемая стоячая волна. Если амплитуды встречных волн одинаковы, то уравнение стоячей волны следующее:
.
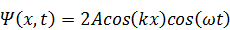Из этого уравнения следует, что амплитуды колебаний в стоячей волне разные в разных точках пространства:
.
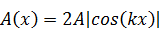В точках, в которых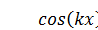 
, а значит, и 
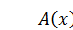, колебания вообще не происходят. Эти точки называются узлами. Кроме того, есть точки, в которых амплитуда колебаний максимальна. В них 
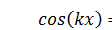и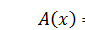 
. В этих точках располагаются так называемые пучности, они являются аналогами максимумов интерференции. Расстояние между ближайшими узлами стоячей волны называется длиной стоячей волныλ с. И оказывается, что длина стоячей волны равна половине длины каждой из встречных бегущих волн:
.
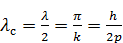| x |
| x 1 |
| Ψ (x) |
| x 2 |
| x 3 |
| t 1 |
| t 2> t 1 |
| t 3> t 2 |
| Фрагмент стоячей волны в три момента времени: t 1, t 2и t 3 |
Ещё одной особенностью стоячей волны является то, что для каждого момента времени фаза колебаний во всех точках между двумя соседними узлами одна и та же, то есть колебания происходят синфазно: во всех точках одновременно колеблющаяся величина Ψ обращается в нуль, одновременно достигает максимума, одновременно достигает минимума. Но в точках по разные стороны от узла колебания происходят в противофазе, то есть с разностью фаз π: если, например, в некоторый момент времени колеблющаяся величина Ψ в точке слева от узла достигла максимума, то в любой точке справа от узла значение Ψ в этот момент времени достигает минимума. Это иллюстрирует следующий рисунок.
На рисунке показаны три состояния фрагмента стоячей волны в области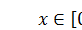 
. В этой области у стоячей волны четыре узла: 
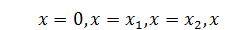и три пучности (между узлами). В областях 
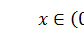и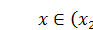 
колебания происходят синфазно, а колебания в области 
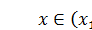происходят в противофазе с колебаниями в первых двух областях.
А теперь вернёмся к координатной пси-функции, то есть к решению СУШ.Для дальнейшего удобно использовать экспоненциальный вид пси-функции частицы в яме, так что:
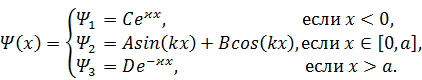
Индексы у коэффициентов A 3и B 3для краткости опущены. Напоминаю, что буквой 𝜘 обозначена величина
.
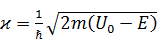