Итак, координатная пси-функция стационарного состояния частицы с учётом квантования энергии имеет следующий вид:
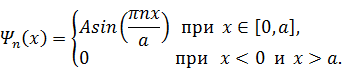
В этом выражении осталась одна не определённая пока константа A. Из уравнения Шрёдингера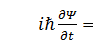 
следует, что пси-функция определена с точностью до произвольного множителя, поэтому константу A можно выбрать произвольно. Этот выбор называется нормировкой пси-функции. Для локализованных (связанных) состояний принято нормировать пси-функцию на единицу:
.
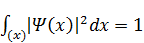Это – уже знакомое вам условие нормировки, которое появляется потому, что квадрат модуля пси-функции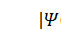 
равен плотности вероятности координаты x. Но если пси-функцию можно умножить на любой постоянный множитель, то придётся считать, что квадрат модуля пси-функции не равен, а только пропорционален плотности вероятности f (x), поэтому и условий нормировки пси-функции может быть несколько. Будем всё же пока использовать нормировку на 1.
.
Таким образом, получаем:
⇒ 
, 
.
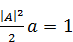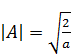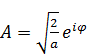Число φ – произвольное, его смысл – начальная фаза колебаний пси-функции. Так как пси-поле частицы в яме представляет собой стоячую волну, то φ в пределах каждого элемента стоячей волны – одно и то же число, которое можно выбрать произвольно, но при переходе в следующий элемент значение φ скачком изменяется на π.
Итак, пси-функция частицы равна:
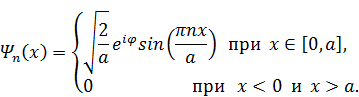
А теперь определим функцию распределения координат частицы.
.
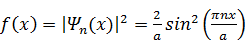Графики функций распределения координат частицы f (x) для первых трёх энергетических уровней имеют вид:
u 4wAAAABJRU5ErkJgglBLAQItABQABgAIAAAAIQCxgme2CgEAABMCAAATAAAAAAAAAAAAAAAAAAAA AABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAA AAAAAAAAOwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAF7kh8odAgAAZAQAAA4AAAAAAAAA AAAAAAAAOgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAKomDr68AAAAIQEAABkAAAAA AAAAAAAAAAAAgwQAAGRycy9fcmVscy9lMm9Eb2MueG1sLnJlbHNQSwECLQAUAAYACAAAACEAFDDe TOEAAAAJAQAADwAAAAAAAAAAAAAAAAB2BQAAZHJzL2Rvd25yZXYueG1sUEsBAi0ACgAAAAAAAAAh AFnq4wEuGQAALhkAABQAAAAAAAAAAAAAAAAAhAYAAGRycy9tZWRpYS9pbWFnZTEucG5nUEsFBgAA AAAGAAYAfAEAAOQfAAAAAA== ">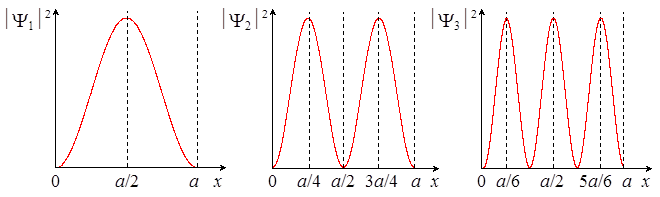 
Какие можно сделать из этих графиков выводы?
|
|
1). Классическая частица в прямоугольной потенциальной яме может с равной вероятностью оказаться в любой части ямы, так как летает с постоянной скоростью от стенки к стенке. Квантовая корпускула ведёт себя сложнее.
· В основном состоянии (n = 1) она стремится быть поближе к центру ямы и очень не любит подходить к стенкам.
· В возбуждённых состояниях она тоже не любит стенок, но кроме того, у частицы появляются некоторые точки внутри ямы, вблизи которых её тоже практически невозможно обнаружить. Эти точки называют узлами пси-поля, так как они являются узлами стоячей пси-волны, которая устанавливается в яме.
2). Существование узлов означает, что пси-поле частицы, находящейся в возбуждённых состояниях, расслаивается на отдельные области (квантуется). Оказывается, что это – общая закономерность микромира, не зависящая от формы потенциальной ямы. Количество слоёв пси-поля равно номеру энергетического уровня n.
Важно заметить, что отличия в поведении классической и квантовой частиц, запертых в потенциальной яме (не только в прямоугольной и бесконечно глубокой) уменьшаются с ростом номераэнергетического уровня. Так проявляется принцип соответствия – результаты квантовой механики в пределе высоких энергий плавно превращаются в результаты классической механики.