| Заданная смешанная система | Результирующие показатели |
 ед. вр.
ед. вр. 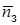

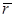
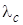
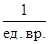
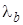
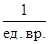 Cобщ
Cобщ
ед. ст.С
ед. ст. 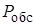
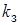

| ед. вр. | |||||||||||
Первонач. Вариант  =____1,333,652,353,650,242,762,710,980,920,611,22 =____1,333,652,353,650,242,762,710,980,920,611,22
| |||||||||||
Вариант а 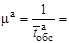 =___0,371,830,461,831,621,381,491,080,461,832,44 =___0,371,830,461,831,621,381,491,080,461,832,44
| |||||||||||
Вариант б 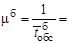 =___1,511,81 =___1,511,81
| 0,46 | 1,81 | 1,64 | 1,36 | 2,1 | 1,54 | 0,45 | 1,81 | 2,41 |
| К вычислению общей стоимости обслуживания заявок в единицу времени |

ед. врем. 
ед. стоим. 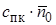
ед. стоим. 
ед. стоим. 
ед. стоим.Cобщ
| ед. стоим. | ||||||
| Первонач. вариант | 1,33 | 1,82 | 0,47 | 0,36 | 0,05 | 2,71 |
| Вариант а | 0,37 | 0,55 | 0,07 | 0,18 | 0,32 | 1,49 |
| Вариант б | 1,51 | 1,45 | 0,14 | 0,18 | 0,33 | 2,1 |
На этом этапе изучается влияние производительности каналов обслуживания на эффективность системы, определяемой показателями С,


 .
.
Исходные данные изучаемой системы:
· λ - интенсивность входного потока,
·  - среднее время обслуживания одной заявки для рассматриваемого варианта системы.
- среднее время обслуживания одной заявки для рассматриваемого варианта системы.
· n = 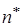 - число каналов обслуживания рассматриваемой смешенной системы совпадает с найденным ранее числом каналов оптимальной системы с отказами.
- число каналов обслуживания рассматриваемой смешенной системы совпадает с найденным ранее числом каналов оптимальной системы с отказами.
·  - признанное оптимальным среднее время пребывания заявки в очереди в смешанной системе с ограничением на время пребывания в очереди (допустимая длина очереди
- признанное оптимальным среднее время пребывания заявки в очереди в смешанной системе с ограничением на время пребывания в очереди (допустимая длина очереди  ).
).
·  - признанная оптимальной допустимая длина очереди в смешанной системе с ограничением на длину очереди (время ожидания заявки в очереди
- признанная оптимальной допустимая длина очереди в смешанной системе с ограничением на длину очереди (время ожидания заявки в очереди  ).
).
· Весовые коэффициенты в формуле (1):
ск = 0,5 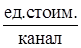 , спк = 0,2
, спк = 0,2 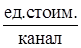 , соч = 0,1
, соч = 0,1  ,
,
сотк = 0,2 ед. стоим.∙ед. врем.
Производительность канала обслуживания определяется величиной параметра 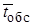 - средним временем обслуживания одной заявки. Рассматривается система, признанная оптимальной (чаще всего - смешанная система). Показатели эффективности этой первоначальной системы сравниваются с аналогичными показателями двух вариантов этой системы:
- средним временем обслуживания одной заявки. Рассматривается система, признанная оптимальной (чаще всего - смешанная система). Показатели эффективности этой первоначальной системы сравниваются с аналогичными показателями двух вариантов этой системы:
Вариант a) системы с уменьшенной производительностью каналов обслуживания за счет увеличения в два раза среднего времени обслуживания и с уменьшенными затратами, связанными с эксплуатацией и простоем оборудования
 ,
,
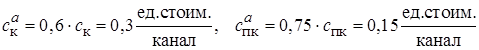 .
.
Вариант b) системы с увеличенной производительностью каналов обслуживания за счет уменьшения в два раза среднего времени обслуживания и увеличенными затратами, связанными с эксплуатацией и простоем оборудования
 ,
,

Выводы к данному разделу работы должны содержать сравнение эффективности трех рассмотренных вариантов системы. Выбрать наилучший вариант, обладающий наименьшей средней стоимостью обслуживания одной заявки в единицу времени С. Отметить, какие имеет этот вариант системы преимущества или недостатки с точки зрения других показателей эффективности как с точки зрения потребителей (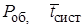 ) с точки зрения потребителей: (
) с точки зрения потребителей: ( ,
,  ), так и с точки зрения эксплуатационных свойств системы: (
), так и с точки зрения эксплуатационных свойств системы: (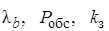 ).
).
Заключение
Итак, проведя анализ полученных результатов, следует сделать следующие заключения:
В соответствии с вариантом задания определены параметры системы λ и  . Задаваясь значениями n (число каналов обслуживания) от единицы до шести, мы вычислили финальные вероятности и в соответствии с ними - показатели эффективности системы. В качестве оптимального числа каналов
. Задаваясь значениями n (число каналов обслуживания) от единицы до шести, мы вычислили финальные вероятности и в соответствии с ними - показатели эффективности системы. В качестве оптимального числа каналов 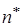 принимаем такое значение n, при котором принимает наименьшее значение средняя стоимость С обслуживания одной заявки в единицу времени (с учетом ограничения
принимаем такое значение n, при котором принимает наименьшее значение средняя стоимость С обслуживания одной заявки в единицу времени (с учетом ограничения  ). Следовательно,
). Следовательно, 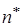 либо точка минимума на графике функции С = С(n), либо
либо точка минимума на графике функции С = С(n), либо 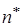 = 6, если С = С(n) - монотонно убывающая функция. В нашем случае n=1.
= 6, если С = С(n) - монотонно убывающая функция. В нашем случае n=1.
В том случае, когда  , т.е. средняя стоимость обслуживания одной заявки в единицу времени смешанной системы меньше соответствующего показателя системы с отказами, наилучшей следует признать смешанную систему.
, т.е. средняя стоимость обслуживания одной заявки в единицу времени смешанной системы меньше соответствующего показателя системы с отказами, наилучшей следует признать смешанную систему.
Список литературы
1. Теория вероятностей и математическая статистика: Учеб. пособие. - М.: ИНФРА - М, 2010. - 287 с. - (Высшее образование).
2. Моделирование систем: Учебник для студентов высш. Учеб. заведений /[С.И. Дворецкий, Ю.А. Муромцев, В.А. Погодин, А.Г. Схиртладзе]. - М.: Изд. Центр «Академия», 2009. - 320 с.
. Овчаров Л.А. Прикладные задачи теории массового обслуживания/ Л.А. Овчаров. М.: Машиностроение, 1969. - 324 с.
. Новиков О.А. Прикладные вопросы теории массового обслуживания/ О.А. Новиков, С.Н. Петухов. М.: Сов. радио, 1969. - 315 с.
. Лифшиц А.Л. Статистическое моделирование систем массового обслуживания/ А.Л. Лифшиц, Э.А. Мальц. М.: Сов. радио, 1978. - 248 с.
. Самусевич Г.А. Основы теории массового обслуживания: учебное пособие / Г.А. Самусевич. Екатеринбург: УГТУ-УПИ, 2005. - 102 с.