Практическая работа
Тема: Решение задач по комбинаторике.
Цель: Закрепление полученных знаний.
Методические рекомендации
Опр.
Перестановками из п разных элементов называются соединения, которые состоят из п элементов и отличаются друг от друга только порядком их расположения.
Число перестановок из п элементов обозначают Р п и вычисляют по формуле Рп = п!
п! (п – факториал) п! = 1·2·3·4·5·… п
Пример. Сколькими способами можно разместить 12 человек за столом, на котором поставлены 12 приборов?
Решение
Р12 = 12! = 1·2·3·4·5·… 12 = 479 001 600 Ответ: 479 001 600
Опр.
Комбинации из т элементов по п элементов, которые отличаются друг от друга или самими элементами или порядком элементов, называются размещениями.
Обозначаются  и вычисляются по формуле
и вычисляются по формуле  ,
, 

Пример
Сколько существует вариантов распределения трёх призовых мест, если в розыгрыше участвуют 7 команд?
Решение
 Ответ: 210 вар
Ответ: 210 вар
Опр.
Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом.
Обозначают  и вычисляют по формуле
и вычисляют по формуле 
Пример
Сколькими способами из колоды в 36 карт можно выбрать 2 карты?
Решение

Ответ: 630 способов
1.Перестановки без повторений Pn= n!
| Решить задачу | ||
| 1. Квартет Проказница Мартышка Осел, Козел, Да косолапый Мишка Затеяли играть квартет … Стой, братцы стой! – Кричит Мартышка, - погодите! Как музыке идти? Ведь вы не так сидите… И так, и этак пересаживались – опять музыка на лад не идет. Тут пуще прежнего пошли у низ раздоры И споры, Кому и как сидеть… Вероятно, музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько? | 5) Сколькими способами можно расставить 5 книг на книжной полке? | |
| 6) Сколько трёхзначных чисел (без повторений цифр) можно составить из цифр 3, 5, 8? | ||
| 7) В семье – 4 человек, а за столом в кухне – 4 стульев. В семье решили каждый вечер, ужиная, рассаживаться на эти 4 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений? | ||
| 8) Пять разных писем раскладывают по одному в пять конвертов. Сколько существует способов такого раскладывания? | ||
| 9) В забеге участвуют 5 спортсменов. Сколькими способами можно распределить их по пяти беговым дорожкам стадиона? | ||
| 10) Сколько стран могут использовать для своего государственного флага три вертикальные полосы одинаковой ширины и разных цветов: белого, красного, синего? | ||
| 2) Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков? | ||
| 11) Сколько существует выражений, тождественно равных произведению abcd, которые получаются из него перестановкой множителей? | ||
| 12) Сколькими способами можно расставить на площадке 6 волейболистов? | ||
| 3) Сколько различных «слов» можно составить из букв слова выбор? | ||
| 4) Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1,2,3,4,5,6, при условии, что цифры в числе не повторяются? | 13) Для дежурства по классу в течение недели (кроме воскресения) выделены 6 учащихся. Сколькими способами можно установить очередность дежурств, если каждый учащийся дежурит один раз? |
2.Размещения без повторений
Если среди n элементов нет одинаковых и повторения одного и того же элемента не допускаются, то число размещений из n элементов по k без повторений определяется формулой 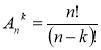
| Решить задачу | |
| 1) На трёх карточках написаны числа 3, 4, 5. Сколько различных двухзначных чисел можно из них составить? | 8) На станции 5 запасных путей. Сколькими способами можно расставить на них 3 поезда? |
| 2) На пяти карточках написаны числа 1, 2, 3, 4, 5. Сколько различных трехзначных чисел можно из них составить? | 9) Сколькими способами можно составить различные двузначные числа из четырех цифр 1,2,3,4 (цифры в числе не повторяются)? |
| 3) Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные? | 10) Набирая номер телефона, абонент забыл две последние цифры. Сколько различных вариантов нужно набрать, чтобы дозвониться, если абонент помнит, что цифры различны? |
| 4) В классе 30 учащихся. Сколькими способами можно выделить для дежурства двух человек, если один из них должен быть старшим? | 11) Сколько различных двухзначных чисел можно образовать из цифр 1,2,3, 5 при условии, что все цифры различны? |
| 5) Нужно выбрать президента общества (25 человек), вице - президента, ученого - секретаря и казначея. Сколькими способами может быть сделан это выбор, если каждый член общества может занимать лишь один пост? | 12) В хирургическом отделении работают 40 врачей. Сколькими способами из них можно образовать бригаду в составе хирурга и ассистента? |
| 6) Учащиеся изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета? | 13) Сколькими способами может разместиться семья из трёх человек в четырёхместном купе, если других пассажиров в купе нет? |
| 7) Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? | 14) Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец? |