Акционерное общество "Меркурий" имеет сорок автоцистерн для перевозки нефтепродуктов. Каждая машина обута в десять шин, запас которых хотя, поэтому желательно иметь в своем распоряжении не слишком больший запас; но при отсутствии шин в запасе акционерное общество терпит убытки из-за невозможности выполнить отдельные заказы на перевозки.
За шинами следит осмотрщик, который по виду шин выносит заключение о ее состоянии. Он подметил, что шина, изношенная на 20% прошла 6000 км; на 40% - 12 000 км; на 60 % - 18 000 км; на 80 % - 24 000 км и на 100 % - 30 000 км. Но, как бы там ни было, не все шины выдерживают 30 000 км.
Исследование, которое проводилось в течение многих лет, показало, что согласно статистике, на 100 шин, введенных в эксплуатацию, 5 выходят из строя после 6000 км, 10 – между 6000 и 12 000 км; 25 – между 12 000 и 18 000 км; 30 – между 18 000 и 24 000 км; 30 между 24 000 и 30 00 км. Таким образом, можно определить кривую продолжительности жизни шин, которая давала бы число шин, находящихся еще в эксплуатации после пробега 6000, 12 000 и т.д. километров.
Дирекция планирует ездки машин на неделю; важно заказывать шины в количестве, достаточном, чтобы произвести вследствие износа или случайного повреждения. Допустим, что машина пробегает за неделю 2000 км; что за неделю дает пробег в 80 000 км для всех машин и 800 000 км для всех шин.
Какой должен быть режим их поступления, или, иными словами, норма поступления запасов?
Вариант 13.1. Решить поставленную задачу рекуррентным способом [10].
Вариант 13.2. Решить поставленную задачу, применяя расчет по математическим ожиданиям [10].
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
1.Сведение к задаче линейного программирования задачи темы 1.
Пример. Пусть три типа судов следует распределить между четырьмя регулярными линиями. В приводимой ниже таблице заданы количества судов каждого типа, месячный объем перевозок каждым судном на каждой регулярной линии и соответствующие эксплуатационные расходы.
| N типа судна Þ N линии ß | Минимальный объем перевозок | |||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| 
| 
| ||
| Число судов |
Составить математическую модель для задачи линейного программирования следующего содержания. Математическую модель составить для двух вариантов: 1.поставлено требование, чтобы в перевозках участвовали все суда; 2. часть судов, при условии выполнения условия минимального объема перевозок разрешается сдавать в аренду.
Обозначим через 
число судов j- го типа (j =1,2,3), которое планируется закрепить за i -й(i -1,2,3,4) регулярной линией.
С учетом введенных обозначений математическая модель задачи для 1-го варианта может быть представлена
найти
при ограничениях
и при 
Последние три ограничения в виде равенств учитывают требования первого варианта о задействовании в перевозке груза всех судов.
Математическая модель для 2-го варианта может быть представлена
и при 
Рекомендация. В большинстве учебных пособий симплекс-метод, метод симплекс-таблиц изложен так, что переменные задачи линейного программирования имеют один индекс, т.е. 
Поэтому имеет смысл ввести новые обозначения в представленных выше математических моделях. Например, для первого варианта:
найти
при ограничениях
и при 
Из сопоставления двух моделей для 
и 
видно, что 
соответствует 
и 
соответствует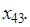 
2.Сведение к задаче линейного программирования задачи темы 2
Пример. Пусть для выполнения некоторой производственной программы, рассчитанной на пять последовательных дней, требуется к началу 
-го дня 
единиц специального инструмента, который к концу дня весь изнашивается, при этом 
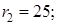
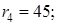
Часть (весь) изношенного инструмента в конце 
-го дня может сдаваться в обычный ремонт, часть (весь) в срочный, а часть (весь) может не сдаваться в ремонт, оставаясь например на складе использованного инструмента.
Пусть обычный ремонт одного инструмента длится 
дня и стоит 
руб., а срочный ремонт одного инструмента длится 
день и стоит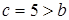 
рублей. Кроме того, один новый инструмент стоит 
рублей.
Составить математическую модель задачи линейного программирования.
Введем следующие обозначения:
число инструментов, покупаемых для использования в 
й день;
число инструментов, сдаваемых в обычный ремонт в конце 
-го дня;
число инструментов, сдаваемых в срочный ремонт в конце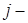 
го дня;
число изношенных инструментов, оставшихся не сданными в ремонт к концу 
го дня.
Тогда число 
инструментов, поступающих в употребление в начале 
го дня, состоит:
из 
инструментов, сданных в обычный ремонт 
дней назад и полученных из ремонта в конце 
го дня;
из 
инструментов, сданных в срочный ремонт 
дней назад и полученных из ремонта в конце го дня;
из 
инструментов, приобретенных к началу 
го дня, т.е.
где 
количество инструмента, купленного для использования в 1-й день; 
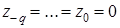, так как до начала выполнения производственной программы в ремонт не мог поступать использованный инструмент и в первые 
дней (в нашем случае 2 дня) еще не поступит из ремонта в употребление ни одного инструмента, сданного даже в срочный ремонт, а в первые 
дней (в нашем случае 3 дня) не поступит в употребление ни одного инструмента, сданного в обычный ремонт.
В конце го дня окажутся использованными 
инструментов, бывших в употреблении в этот день и 
инструментов, оставшихся не сданными в ремонт к концу го дня, т.е.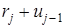 
, из них 
единиц поступает в обычный ремонт, 
единиц - в срочный ремонт и осталось не сданными в ремонт 
единиц инструмента
При этом надо учесть, что инструмент, который возвратится из ремонта в конце 
го (в нашем случае 5-го дня) и позже, уже не понадобится. Поэтому еще за дней (в нашем случае один день) до конца программы не следует сдавать его в обычный ремонт, т.е.
и за 
дней (в нашем случае за два дня) до конца программы не следует сдавать его в срочный ремонт, т.е.
За весь срок выполнения производственной программы будет куплено 
инструментов и израсходовано на это 
рублей; будет сдано в обычный ремонт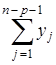 
инструментов и израсходовано 
рублей; будет сдано в срочный ремонт 
инструментов и израсходовано на это 
рублей.
Тем самым задача заключается в минимизации общей стоимости издержек
при ограничениях
и условиях
3.Сведение к транспортной задаче задачи темы 2.
Задача о составлении графика ремонта инструмента может быть сведена к эквивалентной ей транспортной задаче и тем самым для её решения могут быть применены методы решения транспортных задач. Будем считать, что в этой задаче "производится" изношенный инструмент и таких пунктов производства равно 
с "производительностью" в каждом пункте 
изношенного инструмента. Имеется еще один пункт производства инструмента, под которым понимается склад (магазин) с запасом нового инструмента в количестве 
единиц, т.е. если бы перед нами не была поставлена задача минимизации издержек на инструмент, то мы решили бы задачу просто: покупали бы на каждый день новый инструмент.
Имеется 
пунктов потребления и в каждом пункте потребляется или новый инструмент, приобретенный в магазине, или прошедший ремонт (обычный или срочный). Потребность инструмента в каждом пункте потребления равна 
единиц.
Назначим следующие стоимости перевозок 
единицы товара (в нашем случае инструмента) из 
го пункта производства в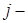 
й пункт потребления
при 
при 
при 
и стоимость перевозки со склада нового инструмента в любой пункт потребления 
Поясним каждое назначение. Первая строчка делает невозможным потребление изношенного инструмента, не прошедшего хотя бы срочного ремонта, длительность которого 
дней. Вторая строка определяет, что изношенный в 
й день инструмент может поступить для использования в 
й день, где 
только после срочного ремонта, так как для го дня, где 
успеет поступить инструмент, который прошел обычный ремонт стоимостью 
Третья строка определяет, что изношенный инструмент в й день может поступить в й день, где 
после обычного ремонта и нет необходимости прибегать к срочному ремонту.
Добавим в качестве пункта потребления склад, куда мы можем отправлять изношенный инструмент в конце каждого рабочего дня, который может быть отправлен на склад без всяких затрат. Подчеркнем, что в рассматриваемом случае склад играет двоякую роль: с одной стороны здесь имеется новый инструмент, стоимость единицы которого 
с другой - на склад отправляется изношенный инструмент, который нет смысла направлять в ремонт (обычный или срочный). Тем самым стоимость перевозки 
означает "перемещение" на складе и поэтому эта стоимость равна нулю.
Пример. Пусть для выполнения производственной программы рассчитанной на пять дней, требуется ежедневно по десять единиц некоторого инструмента, который к концу дня весь изнашивается. Известно, что для выполнения производственной программы, рассчитанной на пять дней, требуется ежедневно по десять единиц некоторого инструмента, который к концу дня весь изнашивается. Известно, что срочный ремонт одного инструмента длится один день и стоит пять рублей; обычной ремонт одного инструмента длится два дня и стоит один рубль, а один новый инструмент стоит шесть рублей.
Задача заключается в обеспечении предприятия инструментом в течение пяти дней при минимальных издержках на его ремонт и покупку.
Условия эквивалентной транспортной задачи представлены в виде следующей таблицы.
 rj
ri
| ||||||
| ∞ | ∞ | |||||
| ∞ | ∞ | ∞ | ||||
| ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ∞ | ∞ | ||
| ∞ | ∞ | ∞ | ∞ | ∞ | ||
Здесь для уравновешивания баланса производства и потребления с потребностью пятьдесят, равной разности между суммарным количеством инструмента, который имеется на складе в качестве нового инструмента плюс изношенный за пять дней, и количеством инструмента, используемого за пять дней; стоимости перевозок в фиктивный пункт потребления равны нулю. Числа в клетках (стоимости перевозок) равны стоимостям обычного или срочного ремонта одного инструмента или покупки одного нового инструмента. Стоимость 
означает, как сказано выше, что инструмент, сданный в ремонт в конце 
го дня, не успеет вернуться к началу 
го дня даже из срочного ремонта (не сможет быть отремонтирован к концу 
дня "ни за какие деньги"); например,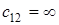 
означает, что инструмент, сданный даже в срочный ремонт в конце первого дня, еще не поступит в употребление во второй день, так как он лишь в конце второго дня вернется из срочного ремонта. При решении транспортной задачи вместо знака ¥ следует поставить, как отмечено выше, число М, которое гораздо больше самой высокой стоимости, которая встречается в исходной задаче.
Решив эту транспортную задачу, мы получим оптимальный план, представленный здесь в виде таблицы.
 rj
ri
| ||||||
Из таблицы следует, что в первые три дня необходимо весь инструмент покупать. В последующие два дня в употребление поступит отремонтированный инструмент, отданный в обычный ремонт в конце первого и второго дня. В третий, четвертый и пятый дни инструмент в ремонт не сдается. Затраты на инструмент составят
Тема 3. Транспортная задача по критерию времени
Покажем на конкретном примере решение транспортной задачи по критерию времени.
Пример. Определить оптимальный план перевозок из условия доставки груза в кратчайший срок при следующих данных. Имеется три пункта производства однородного продукта, в каждом из которых производится количество этого продукта: 
Имеется пять пунктов потребления проводимого однородного продукта с объемом потребления в каждом из них: 
Задана матрица затрат времени на перевозку однородного продукта
где 
время, затрачиваемое на перевозку из 
го пункта отправления в 
й пункт потребления.
Подчеркнем два момента:
а)перевозки считаются законченными, если закончилась самая длительная перевозка;
б)время 
не зависит от количества перевозимого продукта из 
го пункта отправления в 
й пункт потребления.
Решение. Прежде всего заметим, что если определить план перевозок из условия минимизации функции
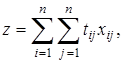
то по этому плану в общем случае продукт потребителю не будет доставлен в кратчайший срок.
Решение задачи начинаем, как обычно, с начального опорного, построенного, например, с помощью метода "северо-западного угла".
Дальнейшие расчеты можно вести одним из двух методов: 1)минимизировать функцию 
но при дополнительных условиях, вводимых последовательно в процессе решения; 2)производить последовательные преобразования решения путем построения так называемых "разгрузочных циклов".
Первый способ. 1-ый шаг. Имеем начальный опорный план
Подчеркиваем в матрице 
все элементы, соответствующие 
плана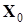 
, и находим среди них наибольший, который обозначим 
, т.е. 
для всех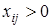 
. Это время определяет срок, в течение которого осуществляются перевозки, соответствующие данному решению. В рассматриваемом примере 
2-ой шаг. Все элементы матрицы, которым соответствуют 
блокируем, то есть заменяем реальные значения 
на произвольно большое число 
В рассматриваемом примере блокированию подлежит элемент, у которого 
3, 
5, куда и заносим вместо 
число 
и тем самым имеем матрицу 
2-ой шаг. Для измененной на 2-ом шаге матрицы 
ищем оптимальное решение, минимизирующее функцию
Это можно сделать, в частности, применяя метод потенциалов. В рассматриваемом примере на предварительном этапе начального опорного плана 
строим матрицу 
. Представим схему, которая соответствует плану 
.
Отсюда
Выделяем в этой матрице отрицательный элемент 
и в матрице 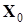строим замкнутый маршрут, затем производим перемещение и получаем план
Преобразуем матрицу 
затем улучшаем план 
до тех пор пока имеется возможность. В рассматриваемом примере получим
Возвращаемся к 1-ому шагу, продолжая расчеты в той же последовательности
1-й шаг. В решении 
элемент 
, т.е. мы освободились от самой длительной перевозки начального плана 
. В плане 
среди 
находим 
В рассматриваемом примере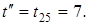 
Поэтому на 2-ом шаге записываем новую матрицу 
в которой элементы 
и 
заменены числом 
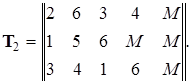
2-ой шаг. Исходя из этой матрицы, применением метода потенциалов находим
И так как в этом плане элементы 
и 
соответствуют блокированным элементам матрицы 
то найденное на предыдущем этапе решение 
является оптимальным решением, исходя из критерия времени. Этому плану соответствует 
Второй способ. 1-ый шаг. Имеем начальный опорный план
Определяем наибольший элемент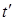 
из всех 
соответствующих 
плана 
и все элементы 
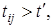соответствующие 
подчеркиваем. В данном примере 
а элементы 
для 
отсутствуют.
2-й шаг. В плане перевозок 
строим "разгрузочный" цикл, начиная с элемента 
, при этом на нечетном местах этого цикла 
, при этом считаем стоящим на первом месте.
В данном случае в "разгрузочный" цикл входят элементы 
Перемещая по этому циклу число 
получим новый план перевозок, равный
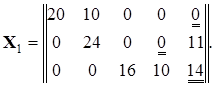
Так как перевозка 
не оказалась равной нулю, то продолжаем построение "разгрузочного" цикла, вновь начиная с элемента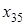 
.
Таковым будет цикл, состоящий из 
Перемещая по этому циклу 
получим новое решение. Как результат такого перемещения 
и тем самым вновь переходим к 1-ому этапу.
1-ый этап. Наибольшим элементом 
для элементов 
плана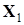 
оказывается элемент 
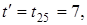поэтому 
и 
подчеркиваем.
2-ый этап. На этом этапе необходимо было бы "разгрузить" элемент 
. Однако построение для нее разгрузочного цикла невозможно. Действительно, если вычесть какое-либо число из элемента 
, то необходимо для сохранения баланса в 5-ом столбце матрицы 
добавить такое же число к другому элементу этого столбца. Но в 5-ом столбце отсутствуют не подчеркнутые элементы. Следовательно, "разгрузить" элемент 
невозможно. На этом основании считаем, что решение, представленное матрицей 
, является искомым оптимальным решением при 
Тема 5. Задача оптимального назначения на авиарейсы
Авиалиния, работающая в течение всей недели, имеет расписание рейсов, приведенное в таблице 5.1.
Поставлена следующая задача. Где должны базироваться экипажи (в пунктах А и/или В) и какие рейсы они должны обслуживать, чтобы суммарное время, которое все экипажи теряют на ожидание обратного рейса, было бы минимальным, но при этом необходимо учесть, что время ожидания каждой бригады должно быть больше 4 часов и меньше 24 часов.
Время 4 часа назначено исходя из того, что экипаж не должен отправляться в обратный рейс, не отдохнув в течение хотя бы четырех часов. Время 24 часа назначено исходя из того, что каждый экипаж не должен ждать рейса более чем сутки; иначе, например, он не сможет налетать то число часов, которое дает право на льготы при выходе на пенсию.
Таблица 5.1
| Пункт А® пункт В | Пункт В® пункт А | ||||
| № рейса | Отправление | Прибытие | № рейса | Отправление | Прибытие |
| 06.00 | 12.00 | 05.30 | 11.30 | ||
| 07.30 | 13.30 | 09.00 | 15.00 | ||
| 11.30 | 17.30 | 15.00 | 21.00 | ||
| 19.00 | 01.00 | 18.30 | 00.30 | ||
| 00.30 | 06.30 | 00.00 | 06.00 |
С целью наилучшего показа сути задачи попытаемся применить метод перебора возможных решений, а затем убедившись, что этот метод требует больших и практически не осуществимых затрат времени, перейдем к рассмотрению венгерского метода, позволяющего решить поставленную задачу.
Предположим, например, что экипаж базируется (живет) в А и обслуживает рейс 3 в направлении В и рейс 102 в противоположном направлении. Этот экипаж должен ждать в пункте В 15.5 часа (от 17.30 до 09.00). Составим путем аналогичных расчетов две матрицы, оформленные в виде таблиц 5.2 и 5.3, элементы которых отражают величины потерянного времени, считая в первом случае, что все экипажи живут в пункте А, а во втором, что все они живут в пункте В. В таблице 5.2. элемент 
время ожидания при обслуживании рейса под номером 
(вылет из пункта проживания А) и обслуживание рейса, номер которого определяется как 
(возвращение в пункт проживания А из пункта В). В таблице 5.3 элемент 
время ожидания при обслуживании рейса под номером 
(вылет из пункта проживания В) и обслуживание рейса, номер которого определяется как 
(возвращение в пункт проживания В из пункта А).
Таблица 5.2
Все экипажи живут в пункте А
| 17.5 | 6.5 | |||
| 19.5 | 1.5 | 10.5 | ||
| 15.5 | 21.5 | 6.5 | ||
| 4.5 | 17.5 | |||
| 2.5 | 8.5 | 17.5 |
Таблица 5.3
Все экипажи живут в пункте B
| 18.5 | 5.5 | |||
| 16.5 | 10.5 | 1.5 | ||
| 20.5 | 14.5 | 5.5 | ||
| 7.5 | 18.5 | |||
| 9.5 | 3.5 | 18.5 |
Составим теперь на основе этих двух таблиц третью (таблица 5.4.), каждый элемент которой будет являться меньшим из чисел, занимающих соответствующие клетки в двух исходных таблицах. При этом мы не будем принимать во внимание числа, которые не превосходят четырех, учитывая потребности экипажа в отдыхе. Например, если нам представится выбор между числами (1, 101; место жительства в пункте А) и (101, 1; место жительства в пункте B), то выбрать следует (1, 101), которое дает нам ожидание в 17,5 часа вместо 18,5 часа. Напротив из (3, 102; место жительство в пункте А) и (102,3; место жительства в пункте B) мы выбираем (3, 102), хотя этому варианту и соответствует меньшее время, т.к. вариант (102,3) оставляет на отдых меньше 4 часов и поэтому неприемлем. Отметим, что время ожидания свыше 24 часов мы предусмотрительно не учитывали в наших таблицах.
Таблица 5.4
| 17,5 | 5,5 | |||
| 16,5 | 10,5 | 10,5 | ||
| 15.5 | 14.5 | 5,5 | ||
| 4.5 | 17.5 | |||
| 9,5 | 8,5 | 17,5 |
Назовем назначением факт приписания экипажа одному из рейсов (скажем (102,1) (3,102), (104,2) и т.д.). Понятно, что каждый экипаж может быть назначен лишь на один прямой и один обратный рейс. Тем самым, любое возможное решение задачи о назначениях может быть представлено таблицей, элементами которой являются числа 0 и 1, причем в каждой строке и в каждом столбце имеется только одна единица, отмечающая выбранное значение. В таблице 5.5 приведен пример возможного решения.
Таблица 5.5
Решение, описываемое таблицей 5.5 соответствует, как можно установить рассматривая и предыдущие таблицы, рейсам (2,101), (102,1), (5,103), (104,3), (105,4), т.е. при таком варианте трем экипажам следует базироваться в пункте А, а двум - в пункте B. Суммарные потери времени будут составлять
15 + 16 + 5,5 + 14 + 12 = 62,5 часа.
В таблице 5.5 показано одно возможное решение, а всего для таблицы с пятью столбцами таких решений может быть 120. Понятно, что с увеличением размерности таблицы число вариантов заставит отказаться от метода перебора, даже имея в распоряжении мощные ЭВМ.
Покажем, как можно решить поставленную выше задачу, применяя алгоритм, в основу которого положен венгерский метод. Нельзя не отметить, что в нашем случае можно было прибегнуть и к методу перебора, решив задачу за несколько часов, а привлекая интуицию, и быстрее. Но оставим другим метод перебора, а сами применим венгерский метод.
Процесс решения расчленяется на шесть этапов.
ЭТАП 1. ПОЛУЧЕНИЕ НУЛЕЙ
Перед тем ознакомиться с процессом решения задачи, отметим, что нуль в последующих таблицах будет иметь другое толкование в сравнении с толкованием в таблице 5.5. Также обратим внимание, что строки последующих таблиц будут обозначаться привычным индексом 
а столбцы - 
Сделав эти предварительные замечания, перейдем к таблице 5.6, которая является копией таблицы 5.3.
Таблица 5.6.
| 17,5 | 5,5 | |||
| 16,5 | 10,5 | 10,5 | ||
| 15.5 | 14.5 | 5,5 | ||
| 4.5 | 17,5 | |||
| 9,5 | 8,5 | 17,5 |
Среди элементов каждого столбца этой таблицы выбираем наименьший и вычтем его из всех элементов этого столбца. Составим таблицу, элементами которой являются разности
где для рассматриваемого случая