Задание 1. Определить зависимость ввода в действие жилых домов от инвестиции в жилищное строительство по регионам РК. Оцените значимость уравнения регрессии и его параметров.
Таблица 5 – Данные для построения уравнения линейной регрессии
| № | Области | Инвестиции, млн.тг, х | Введено, тыс.кв.м., у | (х-хср) | (у-уср) | ỹ | у-ỹ | Аi |
| Акмола | 16,04 | |||||||
| Актобе | 43,37 | |||||||
| Алматы | 75,09 | |||||||
| Атырау | 54,94 | |||||||
| Восточный Казакстан | 25,36 | |||||||
| Жамбыл | 27,36 | |||||||
| Западный Казакстан | 33,73 | |||||||
| Караганды | 9,83 | |||||||
| Костанай | 14,70 | |||||||
| Кызылорда | 21,79 | |||||||
| Мангыстау | 45,77 | |||||||
| Павлодар | 11,65 | |||||||
| Северный Казакстан | 3,07 | |||||||
| Южный Казакстан | 73,85 | |||||||
| Среднее | ||||||||
| σ2 | ||||||||
| r | ||||||||
| R2 | ||||||||
| a | ||||||||
| b |
Требуется:
1. Построить линейное уравнение парной регрессии у от x, определяющее зависимость ввода в действие жилых домов от инвестиции в жилищное строительство.
2. На основе исходных и расчетных значений построить корреляционное поле и тренд уравнения линейной регрессии.
3. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации.
|
|
4. Оценить адекватность модели. Средняя ошибка аппроксимации и коэффициент эластичности.
5. Оценить статистическую значимость параметров регрессии и корреляции.
6. Выполнить прогноз ввода жилья y при прогнозном среднем значении инвестиции x на 20%, Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
7. Добавить в график уравнения линейной регрессии прогнозное значение результативного признака y.
8. С помощью пакета анализа данных (Сервис–Анализ данных–Регрессия) получить параметры линейной регрессии, корреляции, доверительные интервалы, т.е. вывести итоги по регрессионной статистике, дисперсионному анализу и выводу остатков.
Решение:
1. Построить линейное уравнение парной регрессии методом наименьших квадратов.
Используя расчетные формулы:
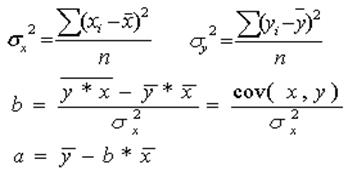
получить уравнение регрессии: ỹ = 16,65 + 0,055 • х.
Вывод: С увеличением инвестиции в строительство жилья на 1млн.тенге ввод жилья незначительно возрастет в среднем на 0,055 кв.м.
3. На диаграмме корреляционного поля зависимости переменных х, у построить ряд точек, используя расчетные значения 
и линию линейного тренда.
Рисунок 5 – Тренд уравнения линейной регрессии у = 16,65 + 0,055 • х
3. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации.
Вывод: Связь прямая положительная. Коэффициент детерминации показывает, что 64% вариации ввода жилья (у) объясняется вариацией инвестиции в строительство х.
4. Оценить качество уравнения регрессии в целом с помощью F-критерия Фишера. Если F< Fтаб, то R2 незначим; если F> Fтаб, то R2 значим.
|
|
Фактическое значение F-критерия: 
сравнивается с табличным значением Fтабл=4,75 из таблицы F-критерия Фишера.
Вывод: Уравнение регрессии значимо при уровне значимости α = 0,05.
5. Оценку адекватности модели определить средней ошибкой аппроксимации:
Рассчитать коэффициент эластичности: 
Показатель эластичности свидетельствует об увеличении на 0,49% ввода кв.м. жилья при увеличении на 1% инвестиции в строительство.
6. Оценку статистической значимости параметров регрессии провести с помощью t-статистики Стьюдента.
Выдвигается основная гипотеза о статистически незначимых показателей
Но: a=b=0.
Определить среднеквадратические отклонения Sa, Sb параметров а и b от своих оценок:
Рассчитать фактические значения t-статистики:
Для числа степеней свободы df=n-2=12 и α=0 tтабл=2,178.
Если tфакт>tтабл, то гипотеза Но отклоняется, т.е. a, b не случайно отличаются от нуля и статистически значимы.
Определить предельную ошибку для каждого показателя:
Доверительные интервалы рассчитать с помощью следующих формул:
Витоге получить аÎ[5.3; 28.0] и b Î[0.03; 0.08]
Вывод: Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью р = 1-a = 0,95, где a=0,05, параметры а и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Выполнить прогноз ввода жилья у при прогнозном среднем значении инвестиции х на 20%. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
|
|
Если прогнозное значение инвестиции составит: 
, то прогнозное значение ввода жилья составит: 
Среднеквадратичное отклонение (ошибка) прогноза:
Предельная ошибка прогноза, которая в 95% случаевне будет превышена, составит: 
Доверительный интервал прогноза 
: [3,09; 68,51]
Добавить в график уравнения линейной регрессии прогнозное значение результативного признака у.
Рисунок 6 – Прогнозное значение на основе линейного уравнения регрессии
8. Вывести итоги по регрессионной статистике, дисперсионному анализу и выводу остатков с помощью команды Сервис–Анализ данных–Регрессия. Получить параметры линейной регрессии, корреляции, доверительные интервалы и остатки.
Задание 2. По данным проведенного опроса восьми групп семей известны данные связи расходов населения на продукты питания с уровнем доходов семьи. Оцените значимость построенного уравнения регрессии и его параметров.
Таблица 6 – Данные для построения уравнения линейной регрессии
| № | Доходы семьи, тыс.тг, х | Расходы на питание, тыс.тг, у | (х-хср) | (у-уср) | ỹ | у-ỹ | Аi |
| 1,2 | 0,9 | ||||||
| 3,1 | 1,2 | ||||||
| 5,3 | 1,8 | ||||||
| 7,4 | 2,2 | ||||||
| 9,6 | 2,6 | ||||||
| 11,8 | 2,9 | ||||||
| 14,5 | 3,3 | ||||||
| 18,7 | 3,8 | ||||||
| Среднее | |||||||
| σ | |||||||
| r | |||||||
| R2 | |||||||
| a | |||||||
| b |
Требуется:
1. Предположим, что связь между доходами семьи и расходами на питание линейная. Построить корреляционное поле.
Рисунок 7 – Корреляционное поле зависимости
2. Расчитать параметры линейного уравнения парной регрессии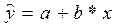 
и получить уравнение 
3. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации
4. Оценить качество уравнения регрессии в целом с помощью F-критерия Фишера. Табличное значение Fтабл =4,75 при k1=1, k2=n-2=6, α = 0,05.
Если F> Fтаб, то уравнение регрессии значимо в целом
5. Качество уравнения регрессии определить средней ошибкой аппроксимации.
6. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитать t- критерий Стьюдента и доверительные интервалы параметров.
Фактические значения t- статистик:
tтабл=2,447 для числа степеней свободы df=n-2=6 и α=0,05.
Для tфакт>tтабл a, b, r статистически значимы.
Рассчитать доверительный интервал для а и b:
В итоге получить: аÎ[0,597; 1,075] и b Î[0,145; 0,191]
7. Найти прогнозное значение результата при значении фактора, составляющем 110% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Если прогнозное значение доходов семьи: 
,
то прогнозное значение расходов на питание составит:
Ошибка прогноза: 
Предельная ошибка прогноза, которая в 95% случаевне будет превышена, составит: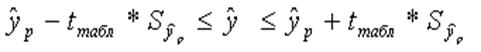 
Вывод: Доверительный интервал прогноза [2,113; 2,867] является статистически надежным.
8. Добавить в график корреляционного поля тренд уравнения линейной регрессии и прогнозное значение результативного признака у.
9. Проверить параметры линейной регрессии, корреляции с помощью пакета Анализ данных командой Сервис– Анализ данных–Регрессия.