Задание 1. Рассчитать показатель выборочной ковариации между потребительскими расходами на связь и среднемесячной абонентской платой за телефон и определить зависимость между ними.
Таблица 1 – Потребительские расходы по связи и среднемесячная
абонентская плата за телефон
| Год | Абонентская плата, тыс.тг., Х | Расходы, тыс.тг, У | (х-хср) | (y-уср) |
| 0,3 | 1,32 | |||
| 0,32 | 1,45 | |||
| 0,34 | 1,77 | |||
| 0,36 | 2,19 | |||
| 0,35 | 2,63 | |||
| 0,35 | 2,82 | |||
| 0,35 | 3,51 | |||
| 0,36 | 4,45 | |||
| 0,43 | 5,65 | |||
| 0,44 | 7,29 | |||
| Среднее значение | ||||
| Cov(x,y) | ||||
| Дисперсия σ2 | ||||
| Коэффициент корреляции, r |
Требуется:
1. Создать таблицу в ячейках А1:Е15 табличного процессора Exсel.
2. Выборочная ковариация является мерой взаимосвязи между двумя переменными и вычисляется по формуле:
 средние значения.
средние значения.
Вычислить ковариацию Cov(x,y), воспользуйтесь встроенной математической функцией СУММПРОИЗВ(ряд1;ряд2).
3. Вычислить дисперсию для ряда х и у по формулам

4. Коэффициент корреляции является более точной мерой зависимости между переменными. Вычислить коэффициент корреляции по следующей формуле:

Задание 2. Вычислить коэффициент корреляции между расходами на питание У и личным доходом Х по данным экономики (усл.ед.) за 5 лет.
Требуется:
1. Представить исходные данные и расчетные показатели в виде следующей таблицы:
Таблица 2 – Исходные данные и расчетные показатели
| год | х | у | (х-хср) | (y-уср) |
| Среднее значение | ||||
| Cov(x,y) | ||||
| Дисперсия σ2 | ||||
| Коэф. корреляции, r |
2. Двумерные данные анализируют с использованием корреляционного поля в координатах У и Х, которая дает визуальное представление взаимосвязи в данных. Данные наблюдений переменных Х, У представить в виде точечного графика – корреляционного поля с помощью команды Вставка – Диаграмма, выбрать тип «Точечная »

Рисунок 1 – Корреляционное поле зависимости
Опишите взаимосвязь.
3. Оценить тесноту связи используя пакет анализа Exсel. Убедитесь, что результаты, вычисленные расчетами и с помощью пакета анализа, совпадают.
Примечание. Коэффициент корреляции можно получить используя пакет анализа Exсel, выполнив команду Сервис–Анализ данных–Корреляция или с помощью статистической функции КОРРЕЛ(рядХ; рядУ)
Задание 3. У 10 магазинов с годовым товарооборотом хi млн.тг (i=1,…,10) численность торговых работников соответственно равна уi. Оценить тесноту связи показателей У и Х по значению коэффициента корреляции.
Исходные данные приведены в таблице:
Таблица 3 – Годовой товарооборот по численности торговых работников
| № | х | у | (х-хср) | (y-уср) |
| Среднее значение | ||||
| Cov(x,y) | ||||
| Дисперсия σ2 | ||||
| Коэф. корр., r |
Требуется:
1. Воспользуйтесь вычислениями и найдите: ковариацию, дисперсию, коэффициент корреляции.
2. Построить диаграмму корреляционнго поля зависимости переменных Х, У, опишите взаимосвязь.
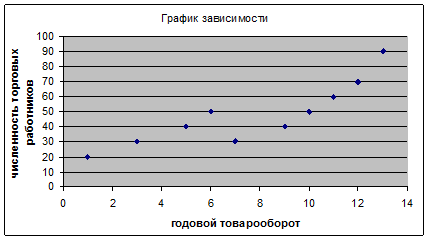
Рисунок 2 – Корреляционное поле зависимости
Задание 4. Определить зависимость ввода в действие жилых домов от инвестиции в жилищное строительство. Известны значения двух признаков по девяти областям РК за определенный год.
Таблица 4 – Сведения по инвестициям в жилищное строительство по регионам РК
| № | Регионы | Инвестиции, млн.тг., х | Введено тыс.кв.м., у | ỹ | Аi |
| Акмола | 0,298 | ||||
| Актобе | 1,922 | ||||
| Алматы | 3,368 | ||||
| Атырау | 5,927 | ||||
| Восточный Казахстан | 0,985 | ||||
| Жамбыл | 7,969 | ||||
| Западный Казахстан | 1,516 | ||||
| Караганды | 0,288 | ||||
| Костанай | 0,228 | ||||
| Кызылорда | 0,420 | ||||
| Мангыстау | 2,457 | ||||
| Павлодар | 0,302 | ||||
| Северный Казахстан | 0,333 | ||||
| Южный Казахстан | 1,880 | ||||
| Среднее | |||||
| σ | |||||
| r | |||||
| R2 | |||||
| a | |||||
| b |
Требуется:
1. Построить диаграмму корреляционного поля.
2. Для характеристики зависимости у от x рассчитать параметры линейной функции. Параметры уравнения регрессии a, b определяют по формулам:

После вычислений должно быть получено уравнение регрессии следующего вида: у =38,81 +28,38*х
3. Тесноту линейной связи и степень вариации оценить с помощью коэффициента корреляции (r) и детерминации (R2). Коэффициент детерминации показывает какой процент вариации У объясняется поведением фактора Х.
Линейный коэффициент парной корреляции: 
Коэффициент детерминации: 
4. В корреляционном поле построить график уравнения регрессии. Для этого:
–по исходным данным добавляется линия тренда с помощью команды Диаграмма–Добавить линию тренда;
–в окне команды Линия тренда выбрать тип тренда «Линейный», и на вкладке Параметры включить параметры показать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимации R2

Рисунок 3 – Окно «Линия тренда»
В результате получить на корреляционном поле график уравнения регрессии:
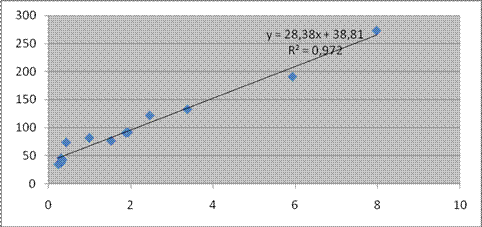
Рисунок 4 – Корреляционное поле зависимости
5. Подставляя в уравнение регрессии фактические значения х, определить теоретические значения  .
.
6. Качество модели определяет средняя ошибка аппроксимации. Оценить модель через среднюю ошибку аппроксимации Ā:

В среднем расчетные значения ỹ для линейной модели отличаются от фактических значений у на 12,51%.