Некоторые значения тригонометрических функций

 

						p		2p
	00	300	450	600	900	1000	2700	3600	1200	1350	1500
							-1
						-1
					¾		¾			-1
	¾					¾		¾		-1

 

7.5. Знаки тригонометрических функций

 

 

Четверть	Величина угла
I	0<α<π/2	+	+	+	+
II	π/2<α<π	+	¾	¾	¾
III	π<α<3π/2	¾	¾	+	+
IV	3π/2<α<2π	¾	+	¾	¾

7.6. Формулы приведения

 

7.7. Выражение тригонометрических функций через одну из них того же аргумента (выбор знака зависит от четверти)

1) через

;

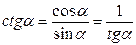
2) через

;

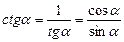
3) через

;

;

4) через

;

;

7.8. Формулы сложения

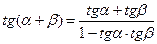
7.9. Формулы двойного аргумента и половинного

;

 

7.10. Преобразование суммы (разности) тригонометрических функций в произведение

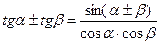
7.11. Преобразование произведения тригонометрических функций
в сумму

7.12. Тригонометрические уравнения

1)
2)
3)
4)

 

7.13. Частные случаи

1)
2)
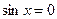
3)

 

7.14. Обратные тригонометрические функции отрицательных аргументов

 

7.15. Тригонометрические неравенства

 

sin x>a

 

 

 

 

 

 

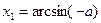
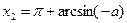
sin x<-a

 

 

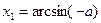
cos x³ a

 

 

cos x< a

 

cos x> -a

 

 

 

cos x£ -a

 

 

 

tg x> a

 

tg x< a

 

 

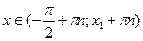
tg x³ -a

 

 

tg x£ -a

 

 

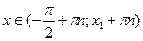
ctg x³ a

 

 

ctg x£ a

 

 

ctg x> -a

 

 

 

ctg x< -a

 

 

Векторы

1.

M(x₀;y₀;z₀)

M₁(x₀;y₀;0)

M₂(0;y₀;z₀)

M₃(x₀;0;z₀)

A(x₀;0;0)

C(0;y₀;0)

B(0;0;z₀)

 

2.

1) Два вектора равны, если они одинаково направлены и равны их модули.

, , тогда

 

2) Модуль вектора (или его длина) вычисляется по формуле:

, то

 

3) Скалярное произведение векторов

, то

 

4) Умножение вектора на число

 

5) Сумма векторов

 

6) Угол между векторами

Если cosj>0, то угол между векторами острый и .

Если cosj<0, то угол j – тупой и .

 

 

7) Направляющие косинусы углов вектора

a, b, g – углы между вектором и положительными направлениями осей координат.

 

Планиметрия

1. Признаки равенства треугольников

Два треугольника равны, если у них соответственно равны:

1 признак – две стороны и угол между ними:

 

2 признак – два угла и прилежащая к ним сторона:

 

3 признак – три стороны:

 

2. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Медианой треугольника наз. отрезок, соединяющий вершину с серединой противоположной стороны.

Биссектриса треугольника делит угол пополам.

 

CD – медиана

В любом треугольнике точка пересечения медиан делит их в отношении 1:2.

OD:CD=1:2

3. Площадь треугольника

 

 

,

где

 

4. Средняя линия треугольника соединяет середины боковых сторон и равно половине основания.

 

 

5. Параллелограмм

Свойства диагоналей параллелограмма:

Сумма квадратов диагоналей равна сумме квадратов всех его сторон.

 

 

 

6. Трапеция

ДК – высота

MN – средняя линия трапеции, соединяет середины боковых сторон и равна полусумме оснований.

MN//DС, MN//AB

 

8. Теорема синусов

 

 

9. Теорема косинусов

 

 

 

Стереометрия

10.1. Призма

Призмой называется многогранник, у которого две грани-равные и параллельные многоугольник, остальные – параллелограммы.

Если боковые ребра призмы ┴ к плоскости основания, то призма прямая, если нет – наклонная. Если в прямой призме основание – правильный многоугольник, то призма правильная.

 

 

10.2. Параллелепипед

Параллелепипедом называется призма, основание которой – параллелограмм, таким образом параллелепипед имеет 6 граней и все они параллелограммы. Противоположные грани равны и параллельны.

Параллелепипед имеет 4 диагонали, все они пересекаются в одной точке
и точкой пересечения делятся пополам.

Прямой параллелепипед, у которого все 6 граней – прямоугольники, называется прямоугольным.

– диагональ

ABCD – диагональное сечение, его площадь

(прямоугольник)

 

Прямоугольный параллелепипед, все грани которого – квадраты, называется кубом.

V= а³, а – ребро куба

10.3. Пирамида

Пирамидой называется многогранник, у которого одна грань – произвольный многоугольник (основание), а все остальные – треугольники с общей вершиной S (боковые грани).

Пирамида называется правильной, если основание ее – правильный многоугольник и высота падает в центр основания. В правильной пирамиде все боковые ребра равны: все боковые грани-равные равнобедренные треугольники.

Высота боковой грани называется апофемой – SM.

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему h.

 

 

10.4. Усеченная пирамида

Если в пирамиде провести сечение A₁B₁C₁ ½½ АВС, то тело, ограниченное этими сечениями называется усеченной пирамидой, параллельные грани называются основаниями.

Δ A₁B₁C₁ – верхнее основание

ΔAВС – нижние основание

ОО₁ – высота усеченной пирамиды.

Усеченная пирамида называется правильной, если из которой она получена, была правильной, все боковые грани правильной усеченной пирамиды – равные, равнобокие трапеции.

,

где Р₁ и Р₂ – периметры оснований,

а = DD₁ – апофема усеченной пирамиды

,

где h = ОО₁ – высота, S₁,S₂ – пощади оснований

 

Цилиндр

Прямым круговым цилиндром называется тело, полученное при вращении прямоугольника ( OBCO₁ ) вокруг одной из его сторон (OO₁) – ось цилиндра, OB – радиус цилиндра, BC – образующая цилиндра, ABCD – осевое сечение цилиндра.

 

 

 

10.6. Конус

Конус, тело полученное при вращении прямоугольного Δ(SOB) вокруг одного из катетов (SO). SO – ось вращения, она же высота конуса, L – образующая конуса,
R – радиус основания.

 

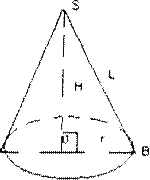
10.7. Усеченный конус

 

10.8. Шар

 

10.9. Шаровой сегмент

Часть шара, отсекаемая от него какой-нибудь плоскостью называется шаровым сегментом. Круг ABCD – основание сегмента, О₁М – высота сегмента (h), М – вершина сегмента.

Кривая поверхность шарового сегмента:

, R – радиус шара

 

 

10.10. Шаровой сектор

Часть шара, ограниченная кривой поверхностью шарового сегмента (АС) и конической поверхностью, основанием которой служит основание сегмента, а вершиной конуса – центр шара, называется.

Кривая поверхность шарового сегмента:

, h – высота сегмента,

R – радиус шара

 

Предел функции

Если существуют пределы:

и , то

1)

2)

3)

4) , А – число

5)

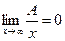
6)

7) – первый замечательный предел

8) – второй замечательный предел

 

Неопределенности, которые нужно раскрывать:

 

Производная

1) Приращением функции y = f(x), связанным с приращением Dх ее аргументах называется разность.

Предел отношения приращения функции к приращению аргумента Dх при произвольном стремлении Dх ®0 называется производной функции y = f(x) в точке х и обозначается: y', f'(x) или .

Таким образом:

Если указанный предел существует, то функцию называют дифференцируемой в точке х.

Производная есть скорость изменения функций в точке х.

Если С – постоянное число, то

1.	4.
2.	5.
3.	6.

7. Если y = f(z), z = φ(x), то есть y = f [ φ(x) ], то функция сложная: