1. 
| 9. 
|
2. 
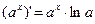
| 10. 
|
3. 
| 11. 
|
4. 
| 12. 
|
5. 
| 13. 
|
6. 
| 14. 
|
7. 
| 15. 
|
8. 
|
Применение производной
2) Если S = S(t) – формула (закон движения точки) пути, то
3) Уравнение касательной к графику функции в точке х0
– это прямая y = kx+b
Следовательно, угловой коэффициент k = f’(x0)=tgα,
α – угол между касательной и положительным направлением оси ОХ.
4) Монотонность функции (возрастание и убывание), экстремумы.
Если f’(х)>0 на некотором отрезке, то функция на данном отрезке возрастает.
Если f’(х)< 0 – то убывает.
Если f’(х0) = 0, то это критическая точка (возможны экстремумы: максимум, минимум).
Если f’(х) в точке x0 меняет знак с « – » на «+»; то x0 – точка минимума.
 |
Если в точке х0 f’(х) в точке x0 меняет знак с «+» на « – »; то x0 – точка максимума.
5) Наибольшее и наименьшее значение функции на отрезке
Чтобы найти наибольшее и наименьшее значение функции на отрезке, нужно:
а) найти производную;
б) найти критические точки,точки, в котором f’(х)=0;
в) найти значения функции в тех критических точках, которые принадлежат данному промежутку и на концах отрезка;
г) из полученных значений выбрать наибольшее и наименьшее значения, записать ответ.
| maxf’(х)= f’(х0)=А [ a, b ] | minf’(х)= f’(х1)=В [ a; b ] |
Первообразная и интеграл
1. Если F(x) является первообразной для функции f(x), то выполняется условие: F’(x)=f(x).
2. Основное свойство первообразных
Если F(x) – первообразная для функции f(x), на промежутке Х, то y функции
y=f(x) бесконечно много первообразных и все они имеют вид y=F(x)+С, где С – любое число.
3. Неопределенный интеграл
Если функция y=f(x) имеет на промежутке Х первообразную y=F(x), то множество всех первообразных, то есть множество функций вида y=F(x)+С называется неопределенным интегралом.
Таблица основных интегралов
1. 
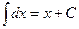
| 6. 
|
2. 
| 7.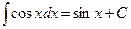 
|
3. 
| 8. 
|
4. 
| 9. 
|
5. 
| 10. 
|
Свойства неопределенного интеграла
1. 
2. 
– постоянный множитель выносится за знак интеграла
3. 
4. Определенный интеграл
– формула Ньютона-Лейбница
а – нижний предел интегрирования
b – верхний предел интегрирования
f(x) – подынтегральная функция
F(x) – первообразная для f(x)
Некоторые постоянные (с точностью до 0,01)
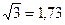
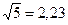
Таблицы квадратов натуральных чисел от 10 до 99
| Десятки | Единицы | |||||||||
Степени числа от 2 до 9
| 22=4 | 32=9 | 42=16 | 52=25 | 62=36 | 72=49 | 82=64 | 92=81 |
| 23=8 | 33=27 | 43=64 | 53=125 | 63=216 | 73=343 | 83=512 | 93=729 |
| 24=16 | 34=81 | 44=256 | 54=625 | 64=1296 | 74=2401 | 84=4096 | 94=6561 |
| 25=32 | 35=243 | 45=1024 | 55=3125 | 65=7776 | 75=16807 | 85=32768 | 95=59049 |
| 26=64 | 36=729 | ||||||
| 27=128 | 37=2187 | ||||||
| 28=256 | |||||||
| 29=512 | |||||||
| 210=1024 |
Ольга Тихоновна Сазонова
математика в формулах
справочник
по дисциплине «Математика»
Подписано к печати
Формат А4. Бумага офсетная. Гарнитура Times New Roman.
Заказ № 137. Тираж 100 экз.
Напечатано в редакционно-издательском отделе
АОУ СПО УР «Ижевский политехнический колледж»
г. Ижевск, ул. Салютовская, 33.
