Краткий перечень основных понятий теории графов.

Краткий перечень основных понятий теории графов.

Теория графов как теоретическая дисциплина может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств (бесконечные графы не будут вводиться в рассмотрение) с заданными отношениями между их элементами. Как прикладная дисциплина теория графов позволяет описывать и исследовать многие физические, технические, экономические, биологические, социальные и другие системы (задача коммивояжера). Например, графом, изображенным на рис. 1, в котором точки − вершины графа − города, линии, соединяющие вершины − ребра − дороги, соединяющие города, описывается так называемая транспортная задача (задача нахождения кратчайшего пути из одного города- пункта в другой).

 

Рис. 1

Графом G называется совокупность двух множеств: вершин V и ребер Х, между элементами которых определено отношение инцидентности – каждое ребро х Х инцидентно двум вершинам v₁ и v₂ Î V,которые оно соединяет. При этом вершина v₁ (v₂) и ребро X называются инцидентными друг другу, а вершины v₁ и v₂, являющиеся для ребра X концевыми точками, называются смежными.

Граф, содержащий направленные ребра с началом v₁ и концом v₂, называется ориентированным графом ( орграфом), а ненаправленные – неориентированным (н-графом). Ребра ориентированного графа называются дугами.

Примеры

1) Ориентированный граф D = (V, X), V ={ v ₁, v ₂, v ₃, v ₄},

X = { x ₁ = (v ₁, v₂), x ₂ = (v ₁, v₂), x ₃ = (v ₂, v₂), x ₄ = (v ₂, v₃)}.

 

Рис. 2

2) Неориентированный граф G = (V, X), V ={ v ₁, v ₂, v ₃, v ₄, v ₅},

X = { x ₁ = (v₁, v ₂), x ₂ = (v₂, v ₃), x ₃ = (v₂, v ₄), x ₄ = (v₃, v ₄)}.

Рис. 3

Одинаковые пары ребер - параллельные или кратные ребра;

Кратностью ребер называют количество одинаковых пар.

 

Рис.4

 

Например, кратность ребра { v ₁, v ₂} в графе, изображенном на рис. 4, равна двум, кратность ребра { v ₃, v ₄} − трем.

Ребро, концевые вершины которого совпадают, называется петлей.

Граф называется конечным, если множество его элементов (дуг и рёбер) конечно, и пустым, если его множество вершин (а, следовательно, и рёбер) пусто.

Граф без петель и кратных рёбер называется полным графом, если каждая пара вершин соединена ребром.

Дополнением графа G называется граф G*, имеющий те же вершины, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получить полный граф.

Степенью ( или валентностью) вершины v Î V н-графа называетсяколичество рёберr(v), инцидентных вершине v.

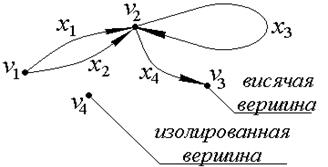
Рис. 5

Вершина графа, имеющая степень 0, называется изолированной, а степень 1 – висячей.

Полустепенью захода (исхода) вершины v ориентированного графа D называется числоd⁺(v) (d^-(v)) дуг ориентированного графа D, исходящих из v (заходящих в v).

Следует заметить, что в случае ориентированного псевдографа вклад каждой петли инцидентной вершине v равен 1 как вd⁺(v), так и вd^-(v). Рассмотрим рис. 5:d⁺(v₂) = 3; d^-(v₂) = 2.

Псевдограф − граф, в котором есть петли и/или кратные ребра.

Мультиграф − псевдограф без петель.

Графы G₁ и G ₂ равны, если их множества вершин и ребер совпадают:

V ₁ = V ₂ и X ₁ = X ₂.

 

Итак, используемые далее обозначения:

V – множество вершин;

Х, Е – множество ребер или дуг;

v (или v_i)– вершина или номер вершины;

G, G ₀ - неориентированный граф;

D, D ₀ – ориентированный;

{ v, w } − ребра неориентированного графа;

{ v, v } – обозначение петли;

(v, w) − дуги в ориентированном графе;

v,w − вершины, x, y, z – дуги и ребра;

n (G), n (D) −количество вершин графа;

m (G) - количество ребер, m (D) - количество дуг.

 

 

Примеры типовых задач:

Рис.6

Пример 1. Задать граф G₁, представ­ленный на рис.6, через множества вер­шин V₁ и ребер E₁.

Граф G₁ может быть полностью оп­ределен:

v Двумя множе­ствами поимено­ванных вершин V₁ = { v₁, v₂, v₃, v₄, v₅ } и поименованных ребер Е₁ = {е₁, e₂, e₃, e₄} (в строгом смысле требуется установление от­ношения инцидентности ребер соответствующим вер­шинам);

v Множеством ребер, каждое из которых представлено па­рой своих концевых вершин: Е= {(v₁, v₂), (v₂, v₃), (v₃, v₄), (v₄, v₅)}.

Порядок указания вершин при описании ребра здесь без­различен, так как все ребра в графе G неориентированные.

 

Рис. 7

Пример 2. На рис.7 изображены графы G₁ - G₁₂ с че­тырьмя вершинами в каждом. Сравнить графы.Результаты сравнения графов таковы:

G₁ - G₇ - неориентированные;

G₈ - G₁₂ - ориентирован­ные;

G₁, G₂ - полные, причем G₁ = G₂;

G₇ - не является полным, так как хотя каждая пара вер­шин и соединена ребром, но имеется одна петля. (Иногда полным называют граф с петлями во всех вершинах, каждая пара которых соединена ребром. Граф G₇ не отвечает и это­му определению. В дальнейшем мы будем придерживаться определения полного графа, данного в начале параграфа.)

G₃ - все вершины этого графа являются изолированными (граф с пустым множеством ребер, т.е. Е = );

G₄ и G₅ являются дополнением друг другу: G₄*= G₅ и G₅*= G₄;

G₆ - мультиграф, так как содержит кратные ребра а и b, a также е и f;

G₈ - ориентированный, канонически соответствующий неориентированному графу G₅;

G₉ и G₁₀ не являются равными, так как имеют отличаю­щиеся ребра: (4, 1) - в G₉ и (1, 4) - в G₁₀;

G₁₁ -ориентированный мультиграф: ребра а и b -крат­ные, тогда как G₁₂ мультиграфом не является, поскольку в нем ребра а и b различно ориентированы.

Рис. 8

Пример 3. Чему равны степени вершин графов G₁, G₃ на рис. 8?

Оба графа имеют по четыре вершины: V= {1, 2, 3, 4}.

Степени вершин неориентированного графа G₁: ρ(1) = 3, ρ(2) = 4, ρ(3) = 3, ρ(4) = 4, если условиться считать вклад петли в степень вершины, равный 2, и ρ(4) = 3, если петля дает вклад 1 в степень вершины. Сумма степеней всех вер­шин графа G₁ равна 14, т.е. вдвое больше числа ребер графа:

где т = 7 - число ребер графа.

Степени вершин ориентированного графа G₃:

ρ₁(1) = 2, ρ₁(2) = 3, ρ₁(3)=1, ρ₁(4)=1;

ρ₂(1)=1, ρ₂(3) = 1, ρ₂(3) = 2, ρ₂(4) = 3.

Суммы степеней вершин первого и второго типа графа G₃ совпадают и равны числу т ребер графа:

 

Задачи для самостоятельного решения.

1. Задать графы G₂ – G₅ (см. рис. 6) множествами их вершин и ребер. Сравнить графы G₁ – G₅ (см. пример 1);

2. Равны ли графы G₁ – G₂ на рис. 8? Задать графы G₁ – G₅ множествами их вершин и ребер. Сравнить графы.

3. Определить дополнение графа G, если:

a) G- пятиугольник;

б) G - треугольник.

4. Какие ориентированные графы канонически соответствуют графам G из заданий 3.а и 3.б (представить графически)?

5. Докажите, что сумма всех степеней вершин графа равна удвоенному количеству рёбер.

 

6. Докажите, что в любом графе количество вершин нечётной степени – чётное число.