Пример решения типовых задач

Пример 1. Какими особенностями отличается граф G, взаимно однозначно соответствующий бинарному отношению R, если R:

а) симметрично;

б) антисимметрично;

в) рефлексивно;

г) антирефлексивно;

д) транзитивно.

Пусть бинарное отношение R определено на множестве V= { v₁,...,v_n }.

а) Симметричному отношению R взаимно однозначно соответствует неориентированный граф без кратных ребер G(R), в котором ребро (v’, v”) существует, если и только если выполнено v’ Rv” (а значит, и v” Rv’ в силу симметричности R).

б) Антисимметричному отношению R взаимно однозначно соответствует ориентированный граф без кратных ребер, не содержащий пар вершин с ребрами, противоположно направленными к разным вершинам.

в) Если R рефлексивно, то граф без кратных ребер имеет петли во всех вершинах.

г) Если R антирефлексивно, то граф G(R) без кратных ребер не имеет петель.

д) Если R транзитивно, то в графе G(R) без кратных ребер для каждой пары ребер (v’, v”) и (v’’, v’’’) имеется замыкающее ребро (v’, v’’’).

Пример 2. Пусть ориентированный граф G на рис.10, б задает отношение R:G(R). Каковы свойства отношения?

Отношение R определено на множестве V={a, b, c, d, e, f} элементов - вершин графа: |V| =6. Свойства отношения:

а)не является рефлексивным, так как отсутствует, например, aRa, bRb.

б)не антирефлексивно, поскольку имеет место cRc, dRd.

в)не является симметричным, так как, например, имеет место aRb но отсутствует bRa.

г)не антисимметрично, поскольку выполняется, например, aRc и cRa.

д)не транзитивно, так как, например, имеется aRb и bRd, но отсутствует aRd.

Пример 3. Каким операциям над графами соответствуют основные операции над отношениями?

1. Пусть 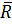- дополнение отношения R на 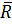= VXV, где U - универсальное (полное) отношение U = VXV, т.е. отношение, имеющее место между любой парой элементов из V.

Граф G (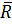) является дополнением графа G(R) (до полного орграфамножеством вершин V и множеством ребер Х(K)=(VXV).

2. Граф обратного отношения G (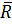) отличается от графа G(R) тем, что направление всех ребер заменены на обратные.

3. Граф объединения двух отношений, заданный на V, G(R₁ R₂) является графом суммы двух графов G(R₁) и G(R₂): G(R₁ R₂) = G(R₁) G(R₂).

4. Граф пересечения отношений R₁∩R₂ на V, G(R₁∩R₂) является графом произведения двух графов G (R₁) и G (R₂): G (R₁∩R₂)= G (R₁) ∩ G (R₂).

Пример 4. Найти декартово произведение графов.

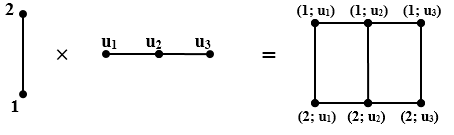
Упражнения

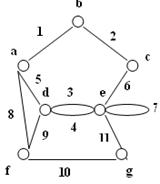Рис. 13	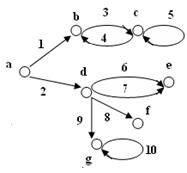Рис. 14
Рис. 15

1. Для графов на рис.13 и 14 задать части H₁ и H₂ такие, что:

o сумма H₁ и H₂ является прямой;

o H₁ и H₂ не пересекаются по вершинам;

o H₁ и H₂ не пересекаются по рёбрам.

2. Для графа G на рис.15:

1) определить, является ли следующая часть H_i (i 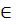{1, 2, …, 5}) графа G подграфом, суграфом, покрывающим суграфом, если:

а) V (H ₁) = {a, b, e, f},

Х(H ₁) = {1, 3, 4, 6};

б) V (H ₂) = {a, b, e, f},

Х(H ₂) = {1, 3, 4, 5, 6, 13};

в) V (H ₃) = {f, G, m, k},

Х(H ₃) = {14, 15, 17, 18, 19, 20, 21, 22};

г) V (H ₄) = {b, c, d, f, g, h},

Х(H ₄) = {2, 7, 9, 11};

д) V (H ₅) = V (G),

Х(H ₅) = {1, 2, 7, 8, 13, 16, 17, 18}.

2) выполнить операции над H ₁, H ₂, H ₃ графа G

3. Пусть множество V ={ v_i }, i =1, 2, 3, 4. На V задано отношение эквивалентности R так, что v_jRv_k, где j, k =1,2,3,4. Какому графу G соответствует отношение R? Задать G графически.

4. Пусть граф G содержит V ={ v₁, v₂, v₃, v₄, v₅ }, X = {(v₁, v₂), (v₁, v₅), (v₂, v₃), (v₂, v₄), (v₃, v₅)}, | V |=5, | Х |=5. Задать граф G графически, а соответствующее ему отношение - матрицей смежности. Каковы свойства данного отношения?

5. Изобразить графы, соответствующие отношениям, представленным следующими матрицами:

R1 a b c d e a           b           c           d           e           А	R2 a b c d e a           b           c           d           e           Б	R3 a b c d e f a             b             c             d             e             f             В
R4 a b c d e f a             b             c             d             e             f             Г	R5 a b c d e f a             b             c             d             e             f             Д

6. Докажите, что граф является пустым тогда и только тогда, когда все его подграфы – тоже пустые.

7. Постройте граф, изображающийотношение делимости на множестве {1,2,3,4,5,6,7,8,9,10}.

8. Докажите, что граф является полным тогда и только тогда, когда все его подграфы, порождённые некоторым множеством вершин – тоже полные.

9. Докажите, что пустой граф с n вершинами содержит ровно n попарно неизоморфных подграфов.

10. Докажите, что граф с n вершинами является пустым тогда и только тогда, когда он содержит ровно n попарно неизоморфных подграфов.

11. Докажите, что граф с n вершинами является полным или пустым тогда и только тогда, когда он содержит ровно n попарно неизоморфных подграфов, порождённых некоторыми множествами вершин.

12. Докажите, что полный граф с n вершинами содержит ровно n попарно неизоморфных подграфов, порождённых некоторыми множествами вершин.

13. Докажите, что подграф H графа G является порождённым множеством своих вершин тогда и только тогда, когда не существует ни одного другого подграфа графа G, для которого H являлся бы остовным подграфом.

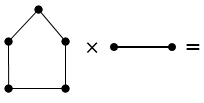
14. Заданы два графа G 1 и G 2. Выполнить G 1 + G 2, G 1 - G 2.

ребра вершины a 1,2 b 2,3 h 2,4 k 3,3 G1

G 2 a b c d

 

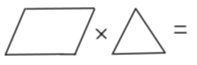
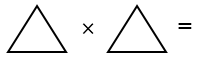
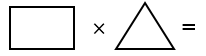
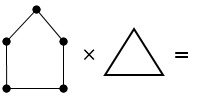
15. Получить ддекартовопроизведение графов.

16. Какие-то две команды набрали в круговом волейбольном турнире одинаковое число очков. Докажите, что найдутся команды А, В и С такие, что А выиграла у В, В выиграла у С, а С выиграла у А.

Маршруты, пути, циклы

Маршрутом в неориентированном графе G называется последовательность вершин и ребер, таким образом, что некоторое ребро Х_i= V _i V _i+1 (i=1,2,…,n).

Пример: В графе, изображенном на рис.3, V ₁ X ₁ V ₂ X ₂ V ₃ X ₄ V ₄ X ₃ V ₂ - маршрут, V ₂ X ₂ V ₃ X ₄ V ₄ – подмаршрут;

Маршрут можно восстановить и по такой записи X ₁ X ₂ X ₄ X ₃;если кратности ребер (дуг) равны 1, можно записать и так V ₁ V ₂ V ₃ V ₄ V ₂.

Маршрут называется цепью, если все ребра различны. Цепь, не пересекающая себя, то есть такая, в которой все вершины встречаются лишь один раз, называется простой цепью.

Маршрут, в котором совпадают начало и конец, называется циклическим.

Циклический маршрут называется циклом, если он является цепью, и простым циклом – если простой цепью.

Вершины V ₁ и V ₂ называются связанными вершинами, если существует маршрут М с началом V ₁ и концом V ₂.

Граф G называется связным, если все его вершины связаны между собой.

Все связанные подграфы графа называются связанными компонентами графа.

Последовательность ребер, в которой конец каждого предыдущего ребра х_i-1 совпадает с началом следующего х_i, называется путем (в нем все ребра проходят по их ориентации).

Путь называется ориентированной цепью, если каждое ребро встречается в нем не более одного раза, и простой цепью, если любая вершина графа G инцидентна не более чем двум его ребрам.

Контур – путь, в котором V ₀= V _k. Контур называется циклом, если он является цепью, и простым циклом, когда это простая цепь.

Граф, не содержащий циклов, называется ациклическим.

Говорят, что вершинаw ориентированного графа D (графа G) достижимаиз вершины V, если либо w = V, либо существует путь (маршрут) из V в w.

Граф (ориентированный граф) называется связным (сильно связным), если для любых двух его вершин V, w существует маршрут (путь), соединяющий V и w. Число ребер маршрута (пути) называется его длиной.

Расстояния в графе

Пусть G=(V, X) - граф (или псевдограф). Расстоянием между вершинами d(v, w) называется минимальная длина пути между ними, при этом d(v, v)=0, d(v, w)=∞, если не Ǝ пути.

Расстояние в графе удовлетворяют аксиомам метрики:

1) ;

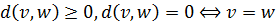2) (не в ориентированном графе);

3) ;

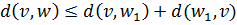4) 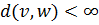в связном графе (не в ориентированном графе).

Пусть G=(V, X) связный граф (или псевдограф).

Диаметром графа G называется величина

.

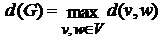Пусть .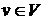

Максимальным удалением(эксцентриситетом) в графе G от вершины v называется величина

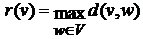
Радиусом графа G называется величина

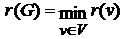
Центром графа G называется любая вершина w 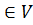такая, что r(w)=r(G).

Множество всех центральных вершин графа называется его центром.

Под длиной (или весом) любого подграфа взвешенного графа будем понимать сумму весов его ребер.

Эйлеровцикл – цикл, содержащий все ребра графа.

Эйлеров граф – граф, имеющий эйлеров цикл.

Эйлерова цепь – цепь, включающая все ребра G -графа, но имеющая различные начало и конец.

Утверждение 1: Для того чтобы связный граф G обладал эйлеровым циклом, необходимо и достаточно, чтобы степени всех его вершин были четными.

Утверждение 2: Для того чтобы связный граф G обладал эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно 2 вершины нечетной степени.

Гамильтонов цикл – простой цикл, проходящий через все вершины рассматриваемого графа.

Гамильтонова цепь – простая цепь, проходящая через все вершины графа, с началом и концом в разных вершинах.