Используем теорию графов для реализации функции алгебры логики с помощью контактных схем.
Назовем контактом проводник, по которому проходит электрический ток.
Построим релейно-контактную схему для следующей функции:
X y 

Если в схеме нет контакта проводников с обмотками реле, то такая схема называется контактной. (схема, изображенная выше, является контактной)
 Если схема является контактной, то ее можно изобразить проще с помощью контактов, которые называются двухполюсниками.
Если схема является контактной, то ее можно изобразить проще с помощью контактов, которые называются двухполюсниками.
Двухполюсники могут соединяться со своими полюсами, образуя контактную схему.
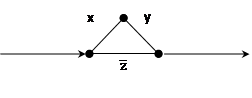 X y
X y 
Это есть ориентированный граф, у которого вершины – это полюса двухполюсников, а ребра – значения логических переменных.
На выходе получаем функцию проводимости этой контактной схемы f (X 1, X 2, …, X n).
Если направление тока изменить, то функция проводимости не изменится.
Граф, представляющий собой контактную схему, может быть мультиграфом.
Любая простая цепь, которая соединяет начальную точку графа с конечной, называется значимой цепью.
Для того, чтобы на выходе был ток, необходимо, чтобы хотя бы 1 значимая цепь проводила ток.
Каждая значимая цепь реализует конъюнкцию, тогда функция проводимости реализует ДНФ.
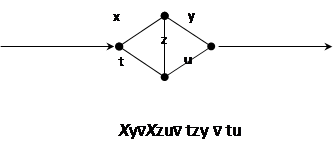
Можно построить заданную схему с наперед заданными свойствами.
Например:
Для комитета из 3х человек для реализации тайного голосования из 3х голосов требуется составить эл. схему. Построить такую схему, чтобы в случае, если член комитета «за» - он нажимал кнопку, если «против» - то не нажимал. Когда большинство «за» - загоралась лампочка
А - 1ый «за»; В – 2ой «за»; С – 3ий «за»; D – результат.

Схему, состоящую из 1 контакта, называют элементарной.
Способы соединения контактов:
· последовательный;
· параллельный.
Контактную схему назовем П-схемой, если она будет получена из элементарных за некоторое конечное число шагов при помощи последовательного и параллельного соединений.


Не любая схема может быть П-схемой.
Одну и ту же схему можно реализовать различным числом контактов. При реализации логической функции желательно строить схему, содержащую минимум контактов.
Схема называется минимальной, если она содержит наименьшее число контактов среди всех схем, имеющих 1 и ту же функцию.

В этой схеме все переменные являются существенными:
| t = z = 0
| y = 1
| X!
|
| t = z = 0
| X = 1
| y!
|
| X = y = z = 0
| t = 1
| u!
|
| X = y = z = 0
| u = 1
| t!
|
| X = y = 1
| u = 0
| z!
|
Поскольку в этой схеме каждой переменной соответствует 1 контакт, то она является минимальной.
Если в схеме все контакты относятся к разным переменным, причем все переменные входят в функцию существенно, то эта функция минимальна.
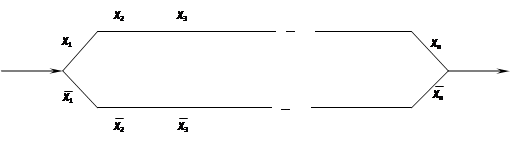
X 1 X 2 … X n  = (X 1
= (X 1  )(X 2
)(X 2  ) … (X n
) … (X n  )
)

Задачи
1. Реализуйте релейно-контактными схемами следующие функции:
а) X yz→t
б) X yz→ X y→ X →y
в) X y  →Xzy
→Xzy
г) (X yz→ X)(y→z)
д) (X →y)(y→z)
e) (X →y)(y→z)→(X →z)
ж) (X →y) →  yz
yz
з) (X →(y→z)) →(y→  )
)
Какие из этих схем можно считать контактными? Нарисуйте соответствующие им контактные схемы.
2. Найдитефункции проводимости для следующих контактных схем:










а) б)












в) г)













д) е)
Если формулы допускают упрощения, то произведите упрощения ипостройте соответствующие упрощенные схемы.
3. Укажите способ реализации функций контактными схемами при помощи КН-форм, аналогичный приведенному в п. 7 способу реализации при помощи ДН-форм.
4. Постройте схему, соответствующую формуле А, заданной таблицей истинности.
5. Из контактов X, y, zсоставьте схему так, что бы она пропустила ток тогда, когда замкнуты какие-нибудь два из этих трех контактов.
6. Постройте контактную схему для игры: «По сигналу каждый игрок замыкает или размыкает переключатель, находящийся под его управлением. Если оба делают одно и то же, то выигрывает игрок А; если они делают противоположное, то выигрывает игрок В». Постройте такую схему, что бы в случае, когда выигрывает игрок А, зажигалась лампочка.
7. Придумайте такую контактную схему, что бы в большом зале можно было включать и выключить свет при помощи любого из четырех переключателей, расположенных на четырех стенах. (Это осуществимо, если свет включается, когда замкнуто честное число переключателей, и выключается, когда замкнуто нечетное число переключателей.Почему это решает задачу?)
8. Комитет состоит из пяти членов. Решения принимаются большинством голосов, однако, если председатель голосует «против», решение не может быть принято. Постройте такую схему, чтобы голосование каждого члена комитета за принятие решения производилось путем нажатия кнопки, а лампочка загоралась в том и только том случае, если решение принято.
9. Постройте такую схему, чтобы экзаменующийся мог отвечать, нажимая кнопки, соответствующие тем вопросам, на которые он хочет дать ответ «да», и чтобы эта схема показывала число правильных ответов с помощью горящей лампочки, соответствующей числам 0, 1, 2, 3, 4, 5 правильных ответов.
10. Докажите, что «мостик» не является П схемой.
11. Постройте заданные схемы:








 Если схема является контактной, то ее можно изобразить проще с помощью контактов, которые называются двухполюсниками.
Если схема является контактной, то ее можно изобразить проще с помощью контактов, которые называются двухполюсниками. X y
X y 






 = (X 1
= (X 1  )(X 2
)(X 2  ) … (X n
) … (X n  )
)
 →Xzy
→Xzy yz
yz )
)








 а) б)
а) б)

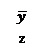












 в) г)
в) г)












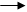

 д) е)
д) е)


