Пример 1. Для вершин V 1 и V 6 графа G на рис.16 привести примеры маршрута, цепи, простой цепи; определить в графе циклический маршрут, цикл, простой цикл, приняв вершину V 1 за их начало и конец.
Для вершин 
:
- маршрут, не являющийся цепью, - (е1, е2, е3, е4, е5, е1, е8, е7, е6, е1, е8, е7) или (е1, е2, е3, е4, е5, е1, е8, е7) и т.п.;
Рис. 16
- цепь, не являющаяся простой цепью, - (е1, е2, е3, е4, е5, е6)
- простая цепь - (е1, е6) или - (е8, е7)
Для вершины V 1:
- циклический маршрут, не являющийся циклом, - (е1, е2, е3, е4, е5, е7, е3, е4, е5, е6, е7, е8, е1, е6, е7, е8)
- цикл, не являющийся простым циклом, - (е1, е2, е3,е4, е5, е6, е7, е8,)
- простой цикл -(е1, е6, е7, е8)
Пример 2. Какими свойствами обладает отношение связанности вершин н-графа на рис. 17? Чему равно число V c связных компонент графа G на рис. 17?
1. Отношение связанности вершин н-графа обладает свойствами:
• рефлексивности: если вершина V 
G связана с какой-либо другой вершиной V ’, то она связана и сама с собой (изолированные вершины также считаются связанными сами с собой);
• симметричности: если в графе G существует маршрут с началом V ’ и концом V ” то существует маршрут с началом V ” и концом V ’;
• транзитивности: если вершина V ’ связана V ”маршрутомM’(e’1,..,e’n), а V ” и V ”’- маршрутом M”(e”1,…,e”p), то V ’ связана с V ”’ маршрутом M(e’1,…,e’n, e”1,…,e”p)
Таким образом, отношение связанности вершин н-графа является отношением эквивалентности, а значит, разбивает все множествовершин V (G) на непересекающиеся подмножества
так что вершины одного и того же множества V i связаны друг с другом, а вершины различных множеств V i и V j не связаны между собой: 
Ø. Поэтому в графе 
нет ребер с концами в различных множествах V i и V j, и он может быть разложен в прямую сумму подграфов
|
|
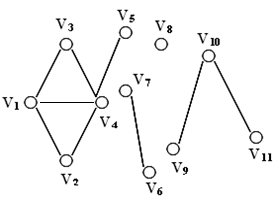
Рис. 17
В графе G на рис. 17 V (G)={ V 1, V 2,…., V 11}. Отношение связанности вершин разбивает G на 4 непересекающихся класса: V 1={ V 1, V 2, V 3, V 4, V 5}, V 2={ V 6, V 7}, V 3={ V 8}, V 4={ V 9, V 10, V 11}.
Поэтому граф G представляет прямую сумму подграфов, являющихся связными компонентами графа G (V):
Таким образом, число связных компонент графа G на рис. 17, V c=4.
Пример 3. Для четырех графов на рис.17 определить расстояния между вершинами. Какие вершины являются центрами графов? Чему равны радиусы графов?
Пусть G 1 - граф с вершинами V 1= { V 1, …, V 5}, G 2 - с вершинами V 2= { V 6, V 7}, G 3 - с вершинами V 3={ V 8}, G 4 - с V 4={ V 9, V 10, V 11}.
Расстояние d(V ’, V ”) между вершинами V ’, V ” как минимальная длина простых цепей с началом V ’и концом V ”(заметим, что d (V ’, V ”)= d (V ”, V ’)
G1= d(V1,V5)=2, d(V1,V4)=1, d(V3,V5)=2 и т.д.;
G2= d(V6,V7)=1, d(V6,V6)=d(V7,V7)=0;
G3= d(V8,V8)=0;
G4= d(V9,V10)=1, d(V9,V11)=2, d(V10,V11)=1, d(V9,V9)=0.
Для определения центров и радиусов графов G 1 – G 4 найдем предварительно для каждого максимальные расстояния R (V ’) от вершины V ’:
G 1= R (V 1) = 2, R (V 2)=2, R (V 3)=2, R (V 4)=1, R (V 5)=2;
G 2= R (V 6)=1, R (V 7)=1;
G 3= R (V 8)=0;
G 4= R (V 9)=2, R (V 10)=1, R (V 11)=2.
Отсюда нетрудно определить радиусы R (G) = min R (V ') и центры G:
R (G 1) = 1, центр - вершина V 4;
R (G 2) = 1, центры - обе вершины V 6, V 7;
R (G 3) = 0, центр - вершина V 8;
R (G 4) = 1, центр - вершина V 10.
Упражнения
Рис. 18
| 
Рис. 19
|
1. Для вершин b, c графа G на рис. 15 привести примеры маршрута, цепи, простой цепи. Привести примеры циклического маршрута, цикла, простого цикла. Существует ли в графе G Эйлеров цикл (цепь), гамильтонов цикл (цепь)?
2. Задача о кёнигсбергских мостах была сформулирована и решена Эйлером в 1736 г. План расположения семи мостов в Кенинсберге XVIII века приведен на рис.18. Задача заключается в том, чтобы пройти каждый мост по одному разу и вернуться в исходную точку. Существует ли такой обход мостов? Решить задачу графически, для чего построить граф задачи, в котором каждая часть города - вершина, а каждый мост - ребро, инцидентное вершинам, относящимся к соединяемым им частям суши.
|
|
3. Какими свойствами характеризуются отношения достижимости вершин в ориентированных графах G 1 – G 3 на рис.19? Какой порядок задают отношения достижимости вершин в G 1 – G 3?
Рис. 20
4. Имеют ли пятигранник-призма и пятиугольник с петлями в некоторых вершинах гамильтонов цикл (цепь)?
5. Построить матрицы смежности и инцидентности графов G 1 - G 10(рис.20). Чему равны степени вершин? Имеют ли графы эйлеров цикл (цепь)? Какому отношению соответствует каждый граф (задать отношение матрицей, определить свойства отношения)? Каковы расстояния между вершинами в графах G 1 - G 7? Какие вершины графов являются центрами? Каковы радиусы этих графов?
6. Для данного графа задать маршруты, цепи, простую цепь, циклический маршрут, цикл, простой цикл:
7. Построить эйлеров цикл для графа:
8. Содержит ли гамильтонов цикл граф ромбического додекаэдра?
9. Определить расстояние между вершинами. Какие вершины можно назвать центрами графа? Чему равны радиусы графа?
10. Докажите, что в связном графе любые две простые цепи максимальной длины имеют общие вершины.
Взвешенные графы
Взвешенный граф − ориентированный граф D =(V, X), на множестве дуг которого определена не которая функция 
, которую называют весовой функцией.Цифра над дугой (см. рис. 6)− вес дуги (цена дуги). Обозначения: для любого пути П нагруженного ориентированного графа D через l (П)определяют сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).Величина l называется длиной пути.
|
|
Рис. 21
Если выбрать веса равными 1, то придем к ненагруженному графу.
Путь в нагруженном ориентированном графе из вершины V в вершину w (Vw), называется минимальным, если он имеет наименьшую длину.
Аналогично определяется минимальный маршрут в нагруженном графе.
Введем матрицу длин дуг C (D)=[ cij ] порядка n, причем
Свойства минимальных путей в нагруженном ориентированном графе:
1) Если для"дуги 
, то"минимальный путь (маршрут) является простой цепью;
2) если v1v2…vk - минимальный путь (маршрут), то для" i, j: 
путь (маршрут) vivi+1…vj-1vj тоже является минимальным;
3) если v…uw − минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k +1 дуг (ребер), то v…u − минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер).
Дерево и лес
Граф G называется деревом,если он является связным и не имеет циклов.
Граф G называется лесом, если все его компоненты связности - деревья.
Вершина v графа называется концевой, если её степень p(v)=1.
Ребро, инцидентное концевой вершине, называется концевым ребром.
Пусть v – вершина дерева G с корнем v 0(V – множество всех вершин, связанных с корнем цепями, проходящими через вершину v). Это множество порождает подграф G (V), называемый ветвью вершины.
Свойства деревьев:
Следующие утверждения эквивалентны:
1) Граф G есть дерево.
2) Граф G является связным и не имеет простых циклов.
3) Граф G является связным и число его ребер ровно на 1 меньше числа вершин.
4) 
две различные вершины графа G можно соединить единственной (и при этом простой) цепью.
5) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл.
Утверждение 3. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина.
Утверждение 4. Пусть G связный граф, а v − висячая вершина в G, граф G’ получается из G в результате удаления вершины v и инцидентного ей ребра. Тогда G’ тоже является связным.
Утверждение 5. Пусть G - дерево с n (G) вершинами и m (G) ребрами. Тогда m (G)= n (G)-1.
Утверждение 6. Пусть G – дерево. Тогда любая цепь в G будет простой.
Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n (G) -1 ребер. Значит, для получения остовного дерева из графа G нужно удалить m(G)-(n(G)-1) ребер.
Число v(G)=m(G)-n(G)+1 − цикломатическое число графа G.