ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ ВРАЩАЮЩИХСЯ ЧАСТЕЙ ЭЛЕКТРИЧЕСКИХ МАШИН

 

Для ЭМ, работающих в режимах с быстро изменявшейся частотой вращения, имеет значение момент инерции J вращающейся части, под которым понимается

,

где m – масса вращающейся части; D – приведенный диаметр.

Для сплошного однородного цилиндра диаметром d, вращающегося вокруг оси, приведенный диаметр равен

.

Для неоднородного тела, каким является вращающаяся часть электрической машины как по форме, так и по материалу, расчетное определение приведенного диаметра представляет трудоемкую работу.

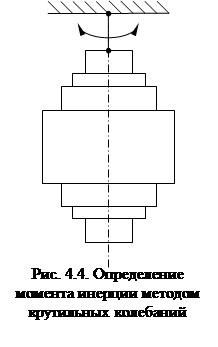
Метод крутильных колебаний пригоден для определения момента инерции относительно легких вращающихся частей; область его применения ограниченамашинами мощностью до 100 кВт с малой вращающейся части не свыше нескольких десятков килограммов. Вращающаяся часть подвешивается в вертикальном положении на струне (рис. 4.4), приводится в крутильное колебательное движение, и определяется период ее малых колебаний, который сравнивается с периодом колебаний эталонного тела с известным моментом инерции, подвешиваемого на этой же струне; тогда искомый момент инерции определится из равенства

,

где J_н – момент инерции эталонного тела; Т_н – его период колебаний; Т – период колебаний данной вращающейся части.

В качестве эталонного тела служит сплошной цилиндр, по массе и диаметру подходящий к испытуемой вращающей части.

Чем длиннее и тоньше струна, тем больше период колебаний и тем точнее его определение, он должен быть не меньше 1 с., диаметр струны – достаточным, чтобы ее растяжение не выходило из предела упругих деформаций, а ее длина ограничивается высотой помещения, в котором производится опыт.

Преимуществом метода является то, что трение практически не влияет на результат опыта, трением о воздух при малых колебаниях можно пренебречь. Однако применение этого метода встречает и некоторые затруднения. Во-первых, точка подвеса должна находиться строго на оси вращения, вращающаяся часть перед опытом должна быть отбалансирована, но результат этого пропадает, если точка подвеса смещена с оси вращения. Во-вторых, чем больше диаметр струны и чем меньше ее длина, тем в большей степени оказывает нежелательное влияние на результат измере­ния ее остаточная деформация от сворачивания в бухту, а рихтовка для устранения такой деформации затруднительна. В третьих, трудно определить период колебаний с достаточной точностью. Когда он мал, удобнее определить по секундомеру продолжительность нескольких периодов, отсчитывая ее между моментами перемены направления вращения.

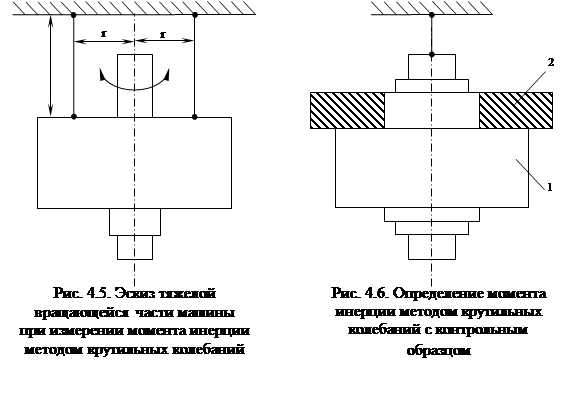Существует разновидность этого метода, состоящая в том, что вращающаяся часть подвешивается не на одной, а на двух струнах. Однако при этом возникает сложность выбрать точки подвеса (рис. 4.5).

В этом случае

,

где m – масса исследуемой вращающейся части; g=9,81 м/с – ускорение земного притяжения. При использовании эталонного тела опыт можно проводить совместно с исследуемым телом (в отличие от рис. 4.4) (рис. 4.6): 1 – исследуемое тело, 2 – контрольный образец.

В этомслучае

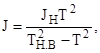
где Т_н.в – период колебаний исследуемой вращающейся части с контрольным образцом.

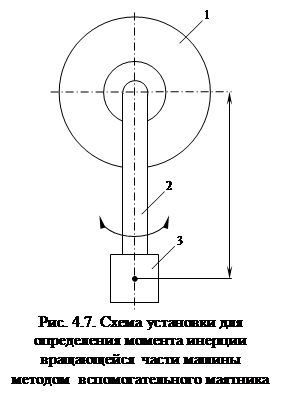
Метод вспомогательного маятника. Может быть применен только к машинам с подшипниками качения, т.е. умеренной мощности. Данный метод не требует выемки вращающегося тела из машины и состоит в том, что к валу при помощи легкого, но не гибкого рычага прикрепляется маятниковая масса m_и (рис. 4.7).

Вся система приводится в колебательное движение отклонением маятника от вертикали. Рекомендуется принимать в расчет два-три самых малых колебаний непосредственно перед их прекращением, но в отличие от предыдущего следует производить измерение продолжительности периодов колебаний прохождением маятника через положение равновесия. Момент инерции определяется по формуле

где m_H – масса маятника; a – расстояние от центра тяжести маятника до оси вращения; T – среднее арифметическое из переменных периодов колебания; g – ускорение свободного падения, равное 9,81 м/с².

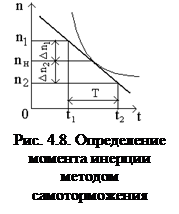Метод самоторможения применяется для наиболее крупных машин, как прокатные двигатели и т.д. и состоит в том, что испытуемая машина приводится во вращение с частотой, превышающей номинальную на 10-15 %,после чего ей предоставляется возможность свободного выбега и произ­водится определение зависимости частоты вращения от времени в интервале 110-115 до 85-90 % ее номинального значения (рис. 4.8).

Кинетическая энергия вращающейся части, равная половине произведения ее момента инерции J на квадрат угловой скорости ω, расходуется на покрытие суммы затормаживающих потерь ∑P, так что

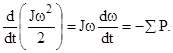
Вместо угловой скорости ω удобнее ввести частоту вращения

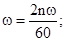
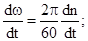
тогда

Здесь 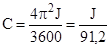носит название постоянной самоторможения.

Если через точки кривой самоторможения с ординатами n_н + ∆n и n_н – ∆n провести секущую, то ее угловой коэффициент равный 2∆n/T, где t – продолжительность самоторможения от n₁ = n_н + ∆n до n₂ = n_н – ∆n, будет очень близок к угловому коэффициенту касательной к кривой в точке n = n_н, т.е.

.

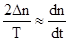Когда машина не возбуждена, то затормаживающим является только механические потери, и при номинальной частоте вращения ∑Р = Р_мех; отсюда

 

и .

 

В опыте можно принимать другие частоты вращения, но тогда необходимо механические потери определить при этих частотах.