Рассмотрим предыдущий пример, добавив вторую факторную переменную – х2 – зарплату сотрудников (табл. 2.1)
Таблица 2.1 – Данные для решения задачи
| у | ||||||||||
| х1 | ||||||||||
| х2 |
Программа EXEL позволяет при построении линейной регрессии большую часть расчетов выполнить очень быстро. Главной задачей остается интерпретация полученных результатов. Предварительно надо ввести исходные данные, обозначив их у, х1, х2.
1. Матрицу парных коэффициентов корреляции можно получить, используя инструмент анализа («Пакет анализа»; «корреляция»). Для этого следует выполнить действия: Сервис → Анализ данных → Корреляция → ОК. появится диалоговое окно, которое надо заполнить в следующем порядке:
- входной интервал: обвести у, х1, х2 вместе, включая заголовки столбцов;
- поставить галочку в окошечке «метки в первой строке»;
- выходной интервал: любая свободная ячейка.
Результат, полученный на компьютере, будет иметь вид таблицы 2.2.
Таблица 2.2
| y | x1 | x2 | |
| y | |||
| x1 | 0,899196 | ||
| x2 | -0,94158 | -0,81501 |
Все значения парных коэффициентов очень высоки, возможна мультиколлинеарность.
Прикладной программы для расчета частных коэффициентов корреляции нет, поэтому рассчитаем их вручную
.
Парные и частные коэффициенты корреляции различаются очень сильно, особенно в третьем случае, что вызвано их высокой взаимной коррелированностью.
2. С помощью инструмента анализа «Регрессия» можно получить результаты регрессионной статистики, дисперсионного анализа, остатки, график подбора линии регрессии, остатков и нормальной вероятности. Порядок действий при этом следующий:
|
|
1) Сервис → Анализ данных → Регрессия → ОК;
2) заполните диалоговое окно:
- входной интервал У – обвести столбец результативного фактора, включая заголовок столбца;
- входной интервал Х – обвести вместе факторные переменные;
- метки – флажок, если первая строка содержит названия столбцов;
- выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона.
Если необходимо получить другую информацию (остатки, график остатков и пр.) надо поставить соответствующий флажок.
После этого нажать кнопку ОК.
Результат работы программы приведен в таблице 2.3, в которой после вывода информации досчитан столбец 
.
Таблица 2.3 – Результаты расчета по программе
| ВЫВОД ИТОГОВ | ||
| Регрессионная статистика 0,968664 | ||
| Множественный R | ||
| R-квадрат | 0,93831 | |
| Нормированный R-квадрат | 0,920684 | |
| Стандартная ошибка | 8,876222 | |
| Наблюдения |
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 8388,489 | 4194,244 | 53,23503 | 5,83E-05 | |
| Остаток | 551,5112 | 78,78731 | |||
| Итого |
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | |
| Y-пересечение | 90,72419 | 24,87448 | 3,64728 | 0,008207 | 31,90544 |
| x1 | 0,88021 | 0,363287 | 2,422909 | 0,045896 | 0,021175 |
| x2 | -7,31879 | 1,907372 | -3,83711 | 0,006399 | -11,829 |
| Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 149,5429 | 31,90544 | 149,5429 |
| x1 | 1,739246 | 0,021175 | 1,739246 |
| x2 | -2,80857 | -11,829 | -2,80857 |
| ВЫВОД ОСТАТКА | ||||
| Наблюдение | Предсказанное Y | Остатки | Y | A |
| 12,64538 | 7,354621 | 0,367731 | ||
| 31,78707 | 3,21293 | 0,091798 | ||
| 43,13494 | -13,1349 | 0,437831 | ||
| 46,689 | -1,689 | 0,037533 | ||
| 65,14499 | -5,14499 | 0,08575 | ||
| 63,01255 | 6,987447 | 0,099821 | ||
| 82,86506 | -7,86506 | 0,104867 | ||
| 92,7662 | -2,7662 | 0,030736 | ||
| 96,32026 | 8,679743 | 0,082664 | ||
| 95,63455 | 4,365448 | 0,039686 | ||
| 1,378417 |
|
|
Уравнение имеет вид: 
.
3. По результатам вывода с компьютера оценим:
а) Множественный коэффициент корреляции 
=0,969, т.е. близок к 1 и свидетельствует о высоком совместном влиянии факторов на результат;
б) Качество уравнения:
- коэффициент детерминации 2 =0,938, т.е. на 93,8% изменения объема предложения связано с изменением цены на товар и зарплатой сотрудников.
- средняя ошибка аппроксимации 
, что больше допустимого (≤8-10%), что говорит о низком качестве уравнения по данному показателю.
в) Оценка надежности уравнения:
- В целом с помощью F-критерия Фишера. Фактическое значение критерия равно 
. Находим по таблице 
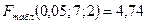. Т.к. Fфакт > Fтабл, то нулевая гипотеза (Н0: R2 =0) о статистической ненадежности отвергается. Уравнения статистически надежно и отражает устойчивую зависимость объема предложения от цены на товар и зарплаты сотрудников.
- Надежность параметров оценивается t-критерием Стьюдента. Получили
. По таблице находим 
. Следовательно все параметры уравнения надежны, т.к все tрасч > tтабл.
4. Получим уравнение регрессии в стандартизованном масштабе. Расчет β- коэффициентов выполним по формулам
.
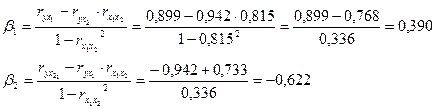Получили уравнение 
.
5. Проведем сравнительный анализ влияния факторов с помощью:
|
|
- частных средних коэффициентов эластичности
.
При увеличении цены на товар на 1% объем продаж увеличивается на 0,44%; а при увеличении зарплаты сотрудников на 1% объем продаж уменьшается на 0,86%. Следовательно, влияние второго фактора выше.
- частных F-критериев. Фактические их значения вычислим по формулам
.
Т.к. оба частных F-критерия больше табличного, то и х1 надо включать после х2, и х2 включать после х1 , т.е. надо использовать уравнение множественной регрессии.
- сравнение β- коэффициентов 
снова подтверждает большее влияние зарплаты сотрудников.
Лабораторная работа №3
Временные ряды
Методические указания
Временной ряд- это совокупность значений исследуемой переменной, расположенной в хронологическом порядке.
Уровни временного ряда – это наблюдения, составляющие временной ряд. Каждый уровень временного ряда формируется из трендовой (Т), циклической(S) и случайной (Е) компонент.
Тренд задает общее направление переменной во времени.
Цикличность – это периодические колебания уровней ряда между двумя вершинами или впадинами (длина цикла).
Случайная компонента делится на спорадические (война,катастрофы и т. д.) и случайный шум как сумма большого числа слабых второстепенных воздействий.
Модели, в которых временной ряд представлен как сумма перечисленных компонент (У=Т+S+E) –аддитивные модели, как произведение (Y=T*S*E) – мультипликативные модели.
Корреляционная зависимость между последовательными уровнями временного ряда (автокорреляция уровней ряда) оценивается коэффициентом корреляции, порядок которого зависит от величины лага- к (смещения во времени).
Коэффициент корреляции оценивает тесноту связи двух рядов:
Так для величины лага к=1 
а
На основании коэффициентов автокорреляции осуществляется анализ структуры временного ряда. Высокое значение r1 свидетельствует о линейном тренде. Если максимальным окажется значение коэффициента автокорреляции порядка l, то исследуемый временной ряд содержит циклическую компоненту. Если ни один из коэффициентов не окажется значимым, то временной ряд не содержит трендовой и циклической компонент и его колебания вызваны случайной компонентой или он содержит сильную нелинейную тенденцию.
Построение модели временного ряда сводится к расчету T,S и Е для каждого уровня временного ряда. В литературе 
рассматриваются методы выделения каждой составляющей.
В дальнейших расчетах будем считать, что сезонная компонента в рассматриваемом ряде отсутствует.
Наличие трендовой компоненты можно выявить:
а) графически, построив ход сглаженных уровней ряда (средних за какой –либо период, отнесенных к середине периода);
б) методом конечных разностей -∆кt,где конечная разность k-того порядка - это разность между соседними конечными разностями порядка k-1.
, т.е.
- первые разности,
- вторые разности, и т. д.
Если конечные разности 1-го порядка равны между собой, то тренд линейный, если 2-го порядка – то параболический.
Построение регрессионной зависимости двух временных рядов требует устранения в каждом из них трендовой и циклической составляющих, так как их наличие скажется на корреляционно-регрессионном анализе.
Для устранения тенденции используют следующие методы.
Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например 
, и расчет отклонений от трендов: 
. Для дальнейшего анализа используют не исходные данные, а отклонения от тренда.
Метод последовательных (конечных) разностей заключается в следующем: если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями- ∆ t, если параболический тренд - вторыми разностями- ∆2t. В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.
Модель, включающая фактор времени, имеет вид
.
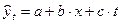Время t включается в уравнение как самостоятельный фактор.
Уравнение регрессии не может быть использовано для прогноза, если в нем не устранена автокорреляция в остатках- корреляционная зависимость между значениями остатков εt за текущий и предыдущие моменты времени.
Для определения автокорреляции остатков используют критерий Дарбина-Уотсона. Проверяют нулевую гипотезу (Н0: r1ε=0) о незначимости коэффициента корреляции остатков. Альтернативные гипотезы Н1 и Н1* состоят, соответственно, в наличие положительной или отрицательной автокорреляции в остатках.
Фактическое значение критерия равно
.
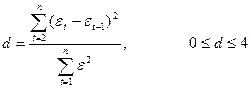По таблице значений статистик Дарбина-Уотсона определяем dl - нижнее и du- верхнее критические значения критерия для числа наблюдений- n, числа независимых переменных- m, и уровня значимости –α.
По этим значениям числовой промежуток разбивается на 5 зон:
Рисунок 3.1 – Зоны критерия Дарбина-Уотсона
Уравнение используется для прогноза только в том случае, если du≤d≤4-du.
Критерий Дарбина-Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением
.