Заданы два временных ряда, представленные в таблице 3.1.
Таблица 3.1 – Временные ряды
| № показателя | t | |||||||||
| Накладные расходы, млн.руб. (у) | ||||||||||
| Реализованная продукция, млн.руб., (х) |
1. Построим график временного ряда для первого показателя. 
Рисунок 3.2 – График эмпирического и сглаженного временных рядов
В целом наблюдается тенденция к увеличению накладных расходов, хотя в третий и седьмой моменты времени происходит их спад.
2. Проведем выравнивание уровней этого ряда методом скользящей средней за три года, для чего воспользуемся формулой
 .
.
Расчет выполним в таблице 3.2, последовательно заполняя ее столбцы.
Таблица 3.2 – Расчетная таблица
| |||||||||||
| 30,667 | |||||||||||
| 35,333 | -7 | -16 | |||||||||
| 41,333 | |||||||||||
| 55,333 | |||||||||||
| 58,333 | |||||||||||
| 67,333 | -21 | -38 | |||||||||
| 76,333 | |||||||||||
| -14 | |||||||||||
| Сум. | |||||||||||
| Сред. | 54,11111 | 8,875 | 3098,88 | 2695,6 |
Нанесем на график (рис.3.2) пунктирной линией скользящие средние. Сглаженным уровням больше всего соответствует линейный тренд.
3. Вычислим значения первых-Δt и вторых-Δ2t разностей (таб.3).Их значения не остаются постоянными, а колеблются вокруг среднего значения, что возможно при наличии линейного тренда.
4. Подсчитаем коэффициент автокорреляции 1-го порядка.
Найдем средние квадратические отклонения:


Тогда
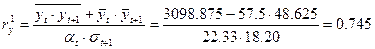 .
.
Связь последующих лет с предыдущими в один лаг тесная (r≥0.7). Возможен линейный тренд.
5. Построим линейную модель зависимости у от х, включив в нее фактор времени. Воспользуемся ппп Excel “Регрессия» (рис.3.3).
Уравнение регрессии имеет вид:
 .
.
| № п/п | у | х | т |
| ВЫВОД ИТОГОВ | ||
| Регрессионная статистика | ||
| Множественный R | 0,929056 | |
| R-квадрат | 0,863145 | |
| Нормированный R-квадрат | 0,817527 | |
| Стандартная ошибка | 10,48184 | |
| Наблюдения |
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 4157,675 | 2078,837 | 18,921049 | 0,002563 | ||||
| Остаток | 659,2142 | 109,869 | ||||||
| Итого | 4816,889 | |||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95,0% | 95,00% | |||
| Y-пересечение | 14,95284 | 7,772958 | 1,9237 | 0,1027377 | -4,0669 | 33,97258 | ||
| х | 1,861831 | 1,651372 | 1,127445 | 0,3026129 | -2,17893 | 5,902594 | ||
| т | -3,79445 | 10,70966 | -0,3543 | 0,7352323 | -30 | 22,41115 | ||
| ВЫВОД ОСТАТКА | ||||||||
| Наблюдение | Предсказанное у | Остатки | εt2 | (εt-εt-1)2 | ||||
| 27,91487 | -0,91487 | 0,836995 | ||||||
| 31,56775 | 4,432249 | 19,64483 | 28,59172 | |||||
| 35,22063 | -6,22063 | 38,69622 | 113,4838 | |||||
| 40,73534 | 0,264663 | 0,070046 | 42,059005 | 2,698401 | ||||
| 49,97371 | 4,026292 | 16,21102 | 14,149853 | |||||
| 59,21208 | 11,78792 | 138,9551 | 60,242884 | |||||
| 70,31228 | -20,3123 | 412,5888 | 1030,423 | |||||
| 79,55065 | 1,449347 | 2,100608 | 473,5685 | |||||
| 92,51269 | 5,487314 | 30,11061 | 16,305174 | |||||
| Σ | 659,2142 | 1778,8239 |
| d= | 2,698401 |
Рисунок 3.3 – Результаты выдачи с компьютера
Множественный коэффициент корреляции R=0.929 свидетельствует о тесной связи у с х и t.
6. Найдем значение критерия Дарбина-Уотсона. Результаты выдачи дополним двумя последними столбцами(ε t2 и (ε t-εt-1)2).
 .
.
По таблице при α=0,05, n=10, m=2 находим:
- верхнее значение du=1.70
- нижнее значение dl=0.63.
Значение критерия попадает в зону 4-du≤d≤4-dl.
Уравнение для прогноза использовать нельзя.
Контрольные вопросы
1. Что такое ряды динамики?
2. Каковы основные элементы временного ряда?
3.Выпишите общий вид аддитивной и мультипликативной моделей временного ряда.
4.Как и для чего проводится сглаживание уровней временного ряда?
5.Что такое лаг?
6.Дайте определение последовательных разностей уровней ряда. Какие выводы можно по ним сделать?
7.Что такое автокорреляция уровней временного ряда и как ее можно оценить количественно?
8.С какими целями проводится выявление и устранение сезонного эффекта?
9.Как структурные изменения влияют на тенденцию временного ряда?
10. Как моделируется тенденция временного ряда?
11. Какова концепция теста Чоу?
12. В чем состоит специфика построения моделей регрессии по временным рядам?
13. Перечислите основные методы исключения тенденции.
14. Изложите суть метода отклонений от тренда.
15. В чем сущность метода последовательных разностей?
16. Какова модель регрессии с включением фактора времени?
17. Охарактеризуйте понятие автокорреляции в остатках. Какие методы ее выявления вам известны?
18. Что такое критерий Дарбина – Уотсона? Изложите алгоритм его применения.
Рекомендуемая литература
Основная литература
1. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002 – 344с.
2. Практикум по эконометрике: Учебное пособие / И.И. Елисева, С.В. Курышева, Н.М. Гордеенко и др; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002 – 192с.
3. Доугерти К. Введение в эконометрику: пер. с англ. – М.: ИНФРА – М, 1999 – 402с.
Экономико-математические методы и прикладные модели: учебное пособие для вузов/ под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999 – 391с.
Дополнительная литература.
1. Грицан В.Н. Эконометрика: учебное пособие. – М.: изд-ий центр «Маркетинг», МУПК, 2001 – 76с.
2. Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование: Учебник – М.: Финансы и статистика. 2001. – 228с.
3. Замков О.О. и др. Математические методы в экономике: Учебник – М.: «Дело и сервис». 1999 – 368с.
4. Макарова В.Н., Трофимец В.Я. Статистика в Excel: Учебное пособие – М.: Финансы и статистика, 2002 – 368с.
Периодическая литература
1. Журнал «Экономика и математические методы».
 № п/п
№ п/п