Имеются статистические данные об объеме предложения товара – у и цены на товар – х. Предполагается линейная зависимость 
.
1. Построим диаграмму рассеяния (х и у из таб. 1.1).
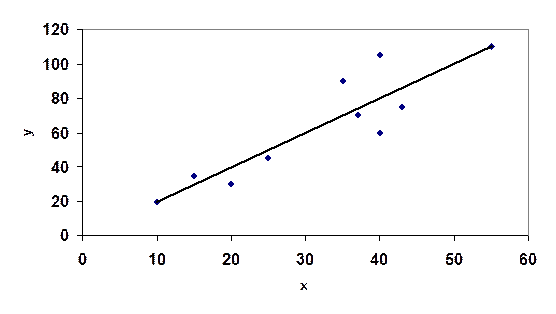
Рисунок 1.1 - Диаграмма рассеяния и линия регрессии
На рисунке в положении точек прослеживается линейная возрастающая зависимость.
2. Необходимые расчеты удобно выполнять на компьютере последовательным заполнением столбцов ниже приведенной таблицы 1.1
После заполнения первых 6-и столбцов надо рассчитать параметры а и в, апотом продолжить заполнение таблицы.
Вычислим
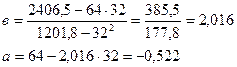
Получено уравнение: 
а) Теснота связи:
Связь тесная (
) и возрастающая (
)
б) Качество уравнения оценивается следующими параметрами:
- Коэффициент детерминации Rух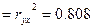 
На 80,8% изменение объема предложения зависит от цены на товар.
- Средний коэффициент эластичности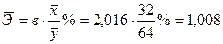 
%.
При увеличении средней цены на товар на 1% средний объем предложений увеличивается на 1,008 %.
-Средняя ошибка аппроксимации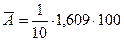 
%=16,09%.
Доля отклонения равна 16,09%, что больше допустимого 8-10%, т.е. качество уравнения низкое.
в) Надежность уравнения проверяется следующим образом.
Надежность уравнения в целом проверим с помощью F-критерия Фишера(Н0: R2=0).
Так как 
, то нулевая гипотеза отвергается, т.е. уравнение надежно и отражает устойчивую зависимость объема предложений от цены на товар. Надежность параметров и коэффициента корреляции оценим с помощью t-критерия Стьюдента (Н0: 
.
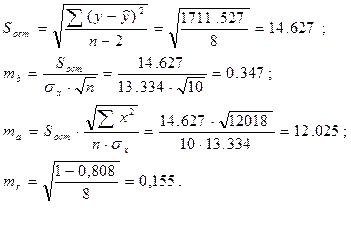
Так как 
, то параметр а получен случайно. Параметр в и коэффициент корреляции надежны т.к.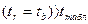 
.
3. Проверим дисперсионное тождество (таб. 1.1)
.
Т.е. 8940 = 7228,47 + 1711,53
8940≡ 8940
4. Построим полученную прямую на диаграмме рассеянья по двум точкам (рис. 1.1.). Например,
|
|
| х | ||
| у | 19,638 | 80,118 |
Точки расположены достаточно близко к линии регрессии.
5. Рассчитаем точечный и интервальный прогноз при γ = 0,9, т.е. хпр на 10% меньше среднего значения
.
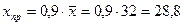Точечный прогноз: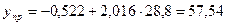 
.
Интервальный прогноз:
- определим среднюю стандартную ошибку прогноза
.
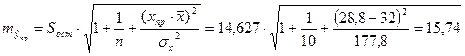Предельная ошибка прогноза
.
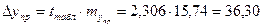При α = 0,05 в 95% случаев прогнозируемое значение – упр – будет попадать в доверительный интервал
Контрольные вопросы
1. Перечислите цели и методы эконометрики.
2. Что такое уравнение регрессии и требования, предъявляемые к включаемым в эконометрическую модель факторам?
3. В чем заключается идея метода наименьших квадратов (МНК)?
4. Поясните экономический смысл параметра b.
5. Что оценивает погрешность ξ?
6. Что такое регрессионное тождество?
7. Как оценивается теснота связи у с х для линейной и нелинейной модели?
8. Как оценивается качество уравнения?
9. Как оценивается надежность уравнения в целом? Какая гипотеза при этом проверяется?
10. Что такое уровень значимости α?
11. Как оценивается значимость параметров и коэффициента корреляции? какая гипотеза проверяется?
12. Сформулируйте условие Гаусса-Маркова.
13. Как осуществляется точечный прогноз по модели?
14. Как осуществляется интервальный прогноз по модели? Что такое доверительный интервал?
15. Какие два класса нелинейных моделей вам известны?
Лабораторная работа № 2
Линейная модель множественной регрессии с двумя факторными переменными
Теоретическая часть
Множественная регрессия – уравнение связи с несколькими независимыми переменными вида
|
|
.
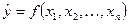Например, линейное уравнение с двумя факторными переменными имеет вид:
(1)
Неизвестные коэффициенты а, в1, в2 оцениваются с помощью классического метода наименьших квадратов (МНК) из системы нормальных уравнений
,
которая может быть решена средствами линейной алгебры.
Для оценки взаимной зависимости случайных величин проводят корреляционный анализ. Рассчитывают определители матрицы парных коэффициентов корреляции – Δr и матрицы межфакторной корреляции – Δr1.
.
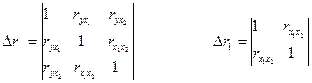Анализ матрицы позволяет выявить между какими факторами связь наиболее тесная у с х1 или у с х2. Высокое значение 
указывает на возможный эффект мультиколлинеарности, т.е. факторы х1 и х2 характеризуют одно и то же.
Чтобы оценить влияние одного фактора на другой при неизменном уровне третьего фактора, рассчитывают частные коэффициенты корреляции (меняются от -1 до +1).
.
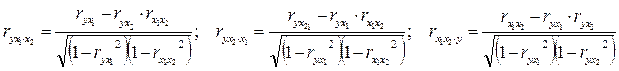Если значения парных и частных коэффициентов корреляции близки, то это говорит о слабой межфакторной связи; если они сильно различаются, то это говорит о сильной межфакторной связи.
Тесноту совместного влияния факторов на результат оценивает коэффициент множественной корреляции
.
Если значение 
> 0,7, то связь тесная.
Качество модели оценивают:
- коэффициент множественной детерминации - 2;
- средняя ошибка аппроксимации - 
.
Значимость уравнения в целом оценивается с помощью F-критерия Фишера (Н0: R2 = 0). Фактическое значение критерия рассчитывается по формуле
.
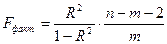Вывод делается на основании сравнения фактического значения с табличным, которое выбирается как Fтабл(α; m; n-m-2).
|
|
Сравнительный анализ влияния факторов в уравнении получают сопоставлением:
- средних частных коэффициентов эластичности показывающих на сколько процентов изменится среднее значение у,если среднее значение соответствующего фактора увеличится на один процент:
;
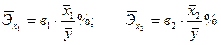- частных F-критериев Фишера, построенных на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Проверяется гипотеза Н0 о несущественности прироста
.
Если Fx факт >Fтабл(α; 1; n-m-2),то хi надо включать в модель после другого фактора, а если Fx факт <Fтабл(α; 1; n-m-2), то нет.
Значимость коэффициентов регрессии оценивается с помощью t- критериев Стьюдента, вычисление которых сводится к приближенной формуле
.
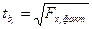Другой вид уравнения регрессии – уравнение регрессии в стандартизованном масштабе
, (2)
где
- стандартизованные переменные, для которых 
;
βi – стандартизованные коэффициенты регрессии.
Стандартизованные коэффициенты определяются МНК из системы
.
по формулам:
Связь между стандартизованными коэффициентами и коэффициентами уравнения в естественных переменных задается соотношением: 
.