3.1 Построение математической модели задачи
| На произв-во изделия А, часов | На произв-во изделия B, часов | Предпр-е предоставит, часов | |
| Оборуд-е 1 го типа | |||
| Оборуд-е 2 го типа | |||
| Оборуд-е 3 го типа | |||
| Прибыль от реализации, за ед. изд-я |
Построение математической модели осуществляется в три этапа:
1. Определение переменных, для которых будет составляться математическая модель.
Так как требуется определить план производства изделий А и В, то переменными модели будут:
x1 - объём производства изделия А, в единицах;
x2 - объём производства изделия В, в единицах.
2. Формирование целевой функции.
Так как прибыль от реализации единицы готовых изделий А и В известна, то общий доход от их реализации составляет 2x1 + 3x2 (рублей). Обозначив общий доход через F, можно дать следующую математическую формулировку целевой функции: определить допустимые значения переменных x1 и x2 , максимизирующих целевую функцию F = 2x1 + 3x2 .
3. Формирование системы ограничений.
При определении плана производства продукции должны быть учтены ограничения на время, которое администрация предприятия сможет предоставить на изготовления всех изделий. Это приводит к следующим трём ограничениям:
x1 + 5x2 £ 10; 3x1 + 2x2 £ 12; 2x1 + 4x2 £ 10.
Так как объёмы производства продукции не могут принимать отрицательные значения, то появляются ограничения неотрицательности:
x1 ³ 0; x2 ³ 0.
Таким образом, математическая модель задачи представлена в виде: определить план x1 , x2 , обеспечивающий максимальное значение функции:
max F = max (2x1 + 3x2 )
при наличии ограничений:
x1 + 5x2 £ 10;
3x1 + 2x2 £ 12;
2x1 + 4x2 £ 10.
x1 ³ 0; x2 ³ 0.
3.2 Решение задачи вручную
Табличный метод ещё называется метод последовательного улучшения оценки. Решение задачи осуществляется поэтапно.
1. Приведение задачи к форме:
x1 + 5x2 £ 10;
3x1 + 2x2 £ 12;
2x1 + 4x2 £ 10.
x1 ³ 0; x2 ³ 0.
2. Канонизируем систему ограничений:
x1 + 5x2 + x3 = 10;
3x1 + 2x2 + x4 = 12;
2x1 + 4x2 + x5 = 10.
x1 ³ 0; x2 ³ 0.
A1 A2 A3 A4 A5 A0
3. Заполняется исходная симплекс-таблица и рассчитываются симплекс-разности по формулам:
d0 = 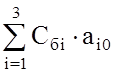 - текущее значение целевой функции
- текущее значение целевой функции
di = 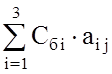 - расчёт симплекс-разностей, где j = 1..6.
- расчёт симплекс-разностей, где j = 1..6.
| C | |||||||
| Б | Cб | A0 | A1 | A2 | A3 | A4 | A5 |
| A3 | |||||||
| A4 | |||||||
| A5 | |||||||
| d | -2 | -3 |
Так как при решении задачи на max не все симплекс-разности положительные, то оптимальное решение можно улучшить.
4. Определяем направляющий столбец j*. Для задачи на max он определяется минимальной отрицательной симплекс-разностью. В данном случае это вектор А2
5. Вектор i*, который нужно вывести из базиса, определяется по отношению:
min 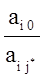 при аi j > 0
при аi j > 0
В данном случае сначала это А3.
5. Заполняется новая симплекс-таблица по исключеню Жордана - Гаусса:
а). направляющую строку i* делим на направляющий элемент:
a i j = a i j / a i j , где j = 1..6
б). преобразование всей оставшейся части матрицы:
a ij = aij - a i j × aij , где i ¹ i* , j ¹ j*
В результате преобразований получаем новую симплекс-таблицу:
| C | |||||||
| Б | Cб | A0 | A1 | A2 | A3 | A4 | A5 |
| A2 | 1/5 | 1/5 | |||||
| A4 | 13/5 | -2/5 | |||||
| A5 | 6/5 | -4/5 | |||||
| d | -7/5 | 3/5 |
Повторяя пункты 3 - 5, получим следующие таблицы:
| C | |||||||
| Б | Cб | A0 | A1 | A2 | A3 | A4 | A5 |
| A2 | 5/3 | 1/3 | -1/6 | ||||
| A4 | 11/3 | 4/3 | -13/6 | ||||
| A1 | 5/3 | -2/3 | 5/6 | ||||
| d | 8 1/3 | -1/3 | 7/6 |
| C | |||||||
| Б | Cб | A0 | A1 | A2 | A3 | A4 | A5 |
| A2 | 3/4 | -1/4 | 3/8 | ||||
| A3 | 11/4 | 3/4 | -13/8 | ||||
| A1 | 7/2 | 1/2 | -1/4 | ||||
| d | 9 1/4 | 1/4 | 5/8 |
Так как все симплекс-разности положительны, то оптимальное решение найдено:
X = (7/2, 3/4, 11/4, 0, 0) (единиц)
max F = 9 1/4 (рублей)