2.1 Задачи на основные понятия и теоремы теории вероятностей
Задача 2.1.1
Покупатель приобрёл телевизор и магнитофон. Вероятность того, что в течение гарантийного срока не выйдет из строя телевизор, равна 0,85, а для магнитофона она равна 0,98. Найти вероятность того, что
а) оба они выдержат гарантийный срок службы;
б) хотя бы один из них не выдержит гарантийного срока службы.
Решение:
Рассмотрим события:
А - в течение гарантийного срока не выйдет из строя телевизор,
В - в течение гарантийного срока не выйдет из строя магнитофон.
По условию задачи
Р (А) = 0,85; Р (В) = 0,98.
а) Пусть событие С заключается в том, что оба они выдержат гарантийный срок службы, тогда С = А · В.
Так как события А и В независимы, то по теореме (13) умножения вероятностей Р (С) = Р (А)· Р (В). То есть Р (С) = 0,85· 0,98 = 0,833 ≈ 83 %.
б) Пусть событие D заключается в том, что хотя бы одно изделие не выдержит гарантийного срока службы. Тогда событие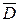 
означает, что оба изделия будут исправны:
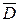= С = А · В, Р (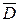) = 0,833. Найдём P (D):
P (D) = 1 – P (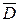) = 1 - 0,833 = 0,167 ≈ 17 %.
Ответ: а) вероятность того, что оба изделия выдержат гарантийный срок службы, равна 83 %; б) вероятность того, что хотя бы одно из них не выдержит гарантийного срока службы, равна 17%.
Задача 2.1.2
Предполагая, что для шахматиста в каждой партии равновероятны три исхода: выигрыш, ничья и проигрыш, найти вероятность того, что из четырёх партий шахматист
а) не проиграет ни одной партии;
б) проиграет хотя бы две партии.
Решение:
а) Рассмотрим события: Н 1 – выигрыш, Н 2 – ничья, Н 3 – проигрыш, В – шахматист не проиграет ни одной партии; Вi – шахматист не проиграет i - ую партию, i = 1, 2, 3, 4.
При этом, Вi = Н 2 + Н 3, а В = В 1 · В 2 · В 3 · В 4. Так как события Вi независимы, то согласно формуле (13), Р (В) = Р (В 1)· Р (В 2)· Р (В 3)· Р (В 4).
|
|
Найдём вероятности событий Вi:
По условию задачи Р (Н 1)= Р (Н 2)= Р (Н 3), а так как эти события образуют полную группу в случае одной партии, то вероятность каждого из них р = 
. Тогда, согласно формуле (10), так как события Н 2 и Н 3 несовместны, Р (Вi)= + = 
. Следовательно, 
б) Пусть события Сi означают проигрыш i партий, i = 0, 1, 2, 3, 4. Тогда событие С – проиграть хотя бы две партии – можно выразить следующим образом:
.
Событием, противоположным С, будет событие 
, при этом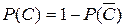 
. Найдём вероятность 
. Так как события 
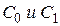несовместны, по теореме сложения вероятностей (10) получим:
. При этом
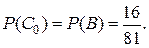
Так как 
для каждой парии, а все партии – независимые испытания, то для отыскания 
можно использовать формулу Бернулли (16):
.
Тогда
а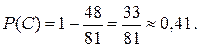 
Ответ: а) вероятность того, что из четырёх партий шахматист не проиграет ни одной партии, равна 20%; б) вероятность того, что из четырёх партий шахматист проиграет хотя бы две партии, равна 41%.
Задача 2.1.3 (о встрече)
Двое приятелей договорились встретиться с 10 до 11 часов в определенном месте, причём пришедший первым ждет в течение 20 минут, после чего уходит. Найти вероятность встречи.
Решение:
Пусть событие А соответствует встрече. Если за х обозначить время прихода первого товарища, а за у – второго, то условие их встречи можно задать системой неравенств:
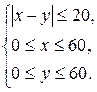
На плоскости хОу область 
, соответствующая общему числу исходов, будет определена системой 
, а область D, соответствующая числу исходов, благоприятствующих событию А, определяется неравенством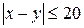 
(рисунок 1).
|
|
Из последнего неравенства получим:
Тогда по определению геометрической вероятности (8), вероятность события А будет равна:
Рисунок 1 – Области для отыскания геометрической
вероятности в задаче 2.1.3
Ответ: вероятность встречи равна 
Задача 2.1.4
Доказать, что для событий А и В выполняется: 
, где 
- невозможное событие.
Решение:
По свойствам действий над событиями (стр. 9) получим:
