Нахождение законов распределения двумерных случайных величин

 

Задача 2.6.1

Найти условный закон распределения случайной величины Х, при условии Y =4, если закон распределения двумерной дискретной случайной величины представлен таблицей 11. Являются ли величины Х и Y независимыми?

 

Таблица 11 – Закон распределения случайной величины (Х, Y)

уj xi
0,1	0,2	0,1	0,1
0,2	0,1	0,2	0,15
0,3			0,05	0,1

 

Решение:

Найдём безусловные законы распределения случайных величин Х и Y. Для этого, дополним таблицу 11 столбцом и строкой, в которой будем находить суммы вероятностей соответственно в строках и в столбцах (см. таблицу 5). Получим таблицу 12.

 

Таблица 12 – Отыскание безусловных вероятностей случайных величин Х и Y по данным задачи 2.6.1

уj xi					Вероятности значений Х
0,1	0,2	0,1	0,1		0,40
0,2	0,1	0,2	0,15		0,45
0,3			0,05	0,1	0,15
Вероятности значений Y	0,3	0,3	0,3	0,1

 

Безусловные законы распределения случайных величин Х и Y оформим в виде таблиц (таблицы 13 и 14 соответственно).

 

Таблица 13 – Безусловный закон распределения случайной величины Х

(в задаче 2.6.1)

Х	0,1	0,2	0,3
Р(Х)	0,40	0,45	0,15

 

Таблица 14 – Безусловный закон распределения случайной величины Y

(в задаче 2.6.1)

Y
Р(Y)	0,3	0,3	0,3	0,1

Используя обозначения таблиц 5 и 6, а также формулу (39), найдём :

При этом выполняется

Условный закон распределения случайной величины Х, при условии Y = 4, можно представить таблицей 15.

 

Таблица 15 – Закон распределения случайной величины Х/ (Y = 4) к задаче 2.6.1

Х	0,1	0,2	0,3

Сравним вероятности значений случайной величины X в условном (табл. 15) и безусловном (табл. 13) законах распределения. Если бы величины Х и Y были независимы, распределение величины X не зависело бы от условий, а вероятности в обоих законах были бы одними и теми же.

Таким образом, сравнивая законы, можно сделать вывод о наличии зависимости между величинами Х и Y.

Замечание: в случае, если условный закон распределения Х при некотором условии совпадёт с её безусловным законом распределения, вывод о независимости величин Х и Y сделать будет нельзя: потребуется проверка всех остальных условий.

Ответ: условный закон распределения случайной величины Х, при условии Y =4, представлен в таблице 15; величины Х и Y зависимы.

Задача 2.6.2

Найти плотности распределения величин Х и Y, если известна их совместная плотность распределения (плотность распределения двумерной случайной величины (Х и Y)):

Решение:

Используя формулы (41) и (42), а также с учётом условий: , получим:

Ответ: плотности распределения величин Х и Y соответственно равны и

 

СПИСОК РЕКОМЕНДУЕМЫХ ИСТОЧНИКОВ

 

1 Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст]: учебное пособие / В.Е. Гмурман. - М.: Высшее образование, 2010. - 479 с.

2 Гнеденко, Б.В. Курс теории вероятностей [Текст]: учебное пособие / Б.В.Гнеденко. - М.: Издательская группа URSS, 2001. - 320 с.

3 Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Текст]: учебное пособие / В.Е. Гмурман. - М.: Юрайт, 2010. - 404 с

4 Вентцель, Е.С. Задачи и упражнения по теория вероятностей [Текст]: учебное пособие / Е.С. Вентцель, Л.А. Овчаров. - М.: Кнорус, 2010. - 480 с.

5 Ивашев-Мусатов, О.С. Теория вероятностей и математическая статистика [Текст]: учебное пособие / О.С. Ивашев-Мусатов. - М.: Издательская группа URSS, 2003. - 224 с.

 

 

Интернет-ресурсы

 

Перечень интернет-ресурсов по теории вероятностей и математической статистике [Электронный ресурс] / Режим доступа: https://zyurvas.narod.ru/resursy.html.

Полный курс лекций по Теории вероятностей [Электронный ресурс]/ НГУ, ред. Н.И. Чернова. – Режим доступа: https://www.nsu.ru/mmf/tvims/chernova/tv99.html.

Готовый учебник по теории вероятностей на русском и английском языках, подготовлен группой ученых ОФИМ СО РАН, интеракивный режим работы, подсказки. – Режим доступа: https://newasp.omskreg.ru/probability.

Сотникова, Н.Я. Первоапрельский задачник по теории вероятностей для студентов нематематиков [Электронный ресурс]/ Режим доступа: https://www.astro.spbu.ru/staff/nsot/Teaching/tver/zadachi.html.

Манита, А.Д. Теория вероятностей и математическая статистика [Электронный ресурс]/ электронная версия учебника. – Режим доступа: https://teorver-online.narod.ru.

ПРИЛОЖЕНИЕ А. Варианты заданий для контрольной работы

Вариант 1

1.1 Известно, что события А и В произошли, а событие С не произошло. Определите, произошло или нет событие .

1.2 На шести карточках написаны буквы «А», «А», «Б», «Б», «Б», «О». Какова вероятность того, что расположенные в ряд наудачу эти карточки составят слово «БАОБАБ»?

1.3 Из урны, в которой находятся десять красных и пять синих шаров, наугад вынимаются три шара. Какой состав шаров по цвету извлечь наиболее вероятно?

1.4 Из интервала [1; 3] наугад выбираются 2 вещественных числа. Найти вероятность того, что их сумма больше 5.

1.5 Известно, что 96% выпускаемых деталей удовлетворяют стандарту. При упрощенном контроле стандартная деталь признается стандартной с вероятностью 98%, а бракованная деталь признается стандартной с вероятностью 5%. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.

1.6 В урне находятся 10 шаров, среди которых половина черных, а остальные белые. 10 раз производится случайная выборка шара из урны с возвратом. Рассчитать вероятность того, что ровно 5 раз был выбран черный шар.

1.7 В партии из 6 деталей имеется 4 стандартные. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины Х – числа стандартных деталей среди отобранных. Найти математическое ожидание и дисперсию случайной величины Х.

1.8 Система (X, Y) имеет плотность распределения , если и , в остальных случаях 0. Найти функцию распределения и вероятность попадания случайной точки (x, y) в прямоугольник , .

Вариант 2

2.1 Докажите, что для событий А и В выполняется равенство .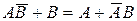

2.2 На шахматную доску произвольным образом поставили две ладьи. Какова вероятность того, что ладьи находятся под ударом друг друга?

2.3 Восемь команд спортсменов разбиваются случайным образом на две группы по четыре команды в каждой группе. Найти вероятность того, что две наиболее сильные команды окажутся в одной группе.

2.4 Определить вероятность того, что корни квадратного уравнения x²+2 a x+ b = 0 являются вещественными, если коэффициенты a и b выбираются наугад из интервала от 0 до 1.

2.5 В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95. Для винтовки без прицела вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведёт один выстрел из наудачу взятой винтовки.

2.6 Вероятность брака равна 0,01. Найти вероятность того, что среди 200 деталей не более двух бракованных.

2.7 Найти дисперсию и среднее квадратичное отклонение случайной величины Х, заданной законом распределения:

Х	- 5
Р	0,4	0,3	0,1	0,2

 

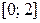2.8 Независимые случайные величины Х и Y равномерно распределены на промежутках и соответственно. Найти их плотности распределения и , функции распределения и , совместную плотность распределения .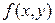

Вариант 3

3.1 Докажите, что для событий А и В выполняется равенство .

3.2 Вероятность отказа каждого прибора при испытании равна 1%. Сколько таких приборов надо испытать, чтобы с вероятностью не менее 90% получить хотя бы один отказ?

3.3 Из колоды карт (52 листа) наудачу извлекаются три карты. Найти вероятность того, что будут вынуты последовательно тройка, семерка и туз.

3.4 В точке С, положение которой на телефонной линии АВ длины L равновозможно, произошёл разрыв. Определить вероятность того, что точка С удалена от точки А на расстояние, не меньшее l (l < L).

3.5 Два автомата производят детали. В продукции первого автомата брак составляет 10%, в продукции второго – 3%. Каждый автомат изготовил по 10 деталей. Какова вероятность, что взятая наудачу деталь окажется бракованной?

3.6 Событие В появится в случае, если событие А наступит не менее 4 раз. Найти вероятность наступления события В, если будет произведено 5 независимых испытаний, в каждом из которых вероятность события А равна 0,8.

3.7 Два стрелка делают по два выстрела. Результаты выстрелов независимы. Вероятность попадания в мишень для первого равна 0,4, для второго – 0,9. Случайная величина Х_i – число попаданий в мишень i –м стрелком, i =1,2. Найти закон распределения случайной величины ; найти М [ ]; D [ ].

3.8 Задана функция распределения двумерной случайной величины (Х, Y): 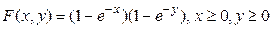. Найти вероятность события, заключающегося в том, что в результате испытания значения Х и Y будут удовлетворять условию: Х < 2, Y < 4.

 

Вариант 4

4.1 Докажите, что событие 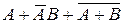достоверно при всех исходах.

4.2 Команде предстоит сыграть полуфинал и, возможно, финал. Вероятность победы в полуфинале равна 0,6, а вероятность победы в финале – 0,5, если игроки выиграют в полуфинале. Какова вероятность того, что команда станет чемпионом?

4.3 В лотерее разыгрывается 100 билетов, а выигрыш приходится на 10. Некто купил 3 билета. Какова вероятность того, что он выиграет хотя бы один билет?

4.4 Случайная точка выбрана наудачу в прямоугольнике со сторонами 1 и 2. Какова вероятность того, что расстояние от этой точки до ближайшей стороны прямоугольника не превосходит 1/3?

4.5 В первой урне 6 белых и 2 чёрных шара, во второй – 3 белых и 4 чёрных. Наудачу выбирается урна, и из неё достают один шар. Он оказался белым. Найти вероятность того, что была выбрана первая урна.

4.6 В партии из 768 арбузов незрелый встречается с вероятностью 0,25. Найти вероятность того, что число зрелых арбузов будет находиться в пределах от 564 до 600.

4.7 Два стрелка делают по два выстрела. Результаты выстрелов независимы. Вероятность попадания в мишень для первого равна 0,6, для второго – 0,1. Случайная величина Х_i – число попаданий в мишень i -м стрелком, i =1,2. Найти закон распределения случайной величины ; найти М [ ]; D [ ].

4.8 Найти функцию распределения двумерной случайной величины, если плотность её распределения , при и , а в остальных случаях 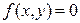. Какова вероятность того, что Х и Y примут значения: .

 

Вариант 5

5.1 Докажите, что для событий А, В и С выполняется равенство .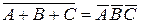

5.2 Сравните между собой вероятности угадывания ровно трех номеров в спортлото «5 из 36» и «6 из 49».

5.3 Из цифр 1,2,3,4,5 выбирается одна, а из оставшихся – другая. Найти вероятность того, что будет выбрана нечетная цифра

а) во второй раз, б) оба раза.

5.4 Точку наудачу бросают в круг радиуса 30 км. Какова вероятность того, что расстояние от точки до центра круга окажется не меньше 5 км, но не больше 10 км?

5.5 В группе две трети студентов – юноши. Вероятность опоздать на занятия для юноши равна 0,2, для девушки – 0,3. Выбранный накануне наугад из списка группы студент опоздал на занятия. Какова вероятность, что это юноша?

5.6 В банк прибыло 1000 стодолларовых купюр. Какова вероятность того, что среди них окажется 5 фальшивых купюр, если 0,1% купюр фальшивые?

5.7 Двое учеников токарей независимо друг от друга сделали по две детали. Вероятность того, что первый изготовит бракованную деталь равна 0,9, а вероятность второго изготовить бракованную деталь – 0,7. Случайная величина Х_i – число бракованных деталей, изготовленных i- м учеником, i =1,2. Найти закон распределения случайной величины ; найти М[ ]; D[ ].

5.8 Случайная величина Х имеет плотность вероятности , (закон Лапласа). Найти коэффициент и функцию распределения.

Вариант 6

6.1 Докажите, что для событий А и В выполняется: .

6.2 Два из трех независимо работающих устройств отказали. Найти вероятность того, что отказали первое и второе устройство, если вероятности отказа устройств равны, соответственно, 10%, 20% и 30%.

6.3 Из урны, в которой находятся три красных, три зеленых и три синих шара, наугад вынимаются три шара. Какова вероятность того, что вынутые шары имеют различные цвета?

6.4 В квадрате со стороной 5 см расположены четыре монеты радиуса 1 см. В квадрат наудачу бросают точку. Определить вероятность того, что эта точка упадёт на одну из монет, если монеты не перекрываются.

6.5 Группа из 25 студентов, среди которых 12 хорошистов и 5 отличников, сдаёт экзамен. Хорошист может с равной вероятностью получить «4» или «5», отличник обязательно получит «5», остальные студенты не могут получить «5». Наугад выбранный студент получил «5». Какова вероятность, что он отличник?

6.6 Вероятность появления события в каждом испытании постоянна и равна р =0,8. Найти вероятность того, что событие в серии из 100 испытаний появится не менее 70 раз.

6.7 Двое токарей независимо друг от друга сделали по одной детали. Вероятность первого изготовить бракованную деталь – 0,1, второго – 0,3. Случайная величина Х_i – число годных деталей, изготовленных i –м токарем, i = 1,2. Построить график функции распределения случайной величины ; найти М [ Y ]; D [ Y ].

6.8 Пусть случайная величина Х имеет плотность распределения f (x):

Найти параметр с, функцию распределения случайной величины Х, построить график функции распределения.

Вариант 7

7.1 Докажите что для событий А и В выполняется: .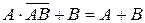

7.2 Сколько раз надо бросить монету, чтобы с вероятностью не меньшей 99% утверждать, что «герб» выпадет хотя бы один раз?

7.3 Двое поочередно бросают монету, причем выигрывает тот, у кого раньше появится герб. Найти вероятность выигрыша второго игрока.

7.4 Из множества наудачу выбрано число , после чего составлено уравнение 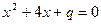. Какова вероятность, что корни этого уравнения окажутся действительными числами?

7.5 В команде двое стрелков стреляют из винтовки и попадают по мишени в 80% случаев, остальные трое стреляют из обреза и попадают в 60% случаев. Наугад выбранный стрелок попал по мишени. С какой вероятностью он стрелял из винтовки?

7.6 Всхожесть семян имеет вероятность 0,8. Найти вероятность того, что из 5 посеянных семян взойдёт не менее 4?

7.7 В опыте 2 раза бросают игральный кубик. Пусть случайная величина Х - разность очков при первом и втором бросаниях. Составить закон распределения случайной величины Х и найти М [ Х ]; D [ Х ].

7.8 Случайная величина Х имеет плотность распределения f (x):

Найти параметр с, функцию распределения случайной величины Х, построить график функции распределения.

Вариант 8

8.1 Докажите, что для событий А, В и С выполняется: .

8.2 При бросании трех игральных костей выпало 11 очков. Какова вероятность того, что на одной из костей выпала «шестерка»?

8.3 В читальном зале 6 учебников по теории вероятностей, из которых 3 в переплёте. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в переплёте.

8.4 Две одинаковые монеты радиуса 1 расположены внутри круга радиуса 2, в который наудачу бросают точку. Определить вероятность того, что эта точка упадёт на одну из монет, если монеты не перекрываются.

8.5 В первой урне находится один белый и 9 черных шаров, а во второй –один черный и 5 белых. Из каждой урны удалили случайным образом по одному шару, а оставшиеся шары ссыпали в третью (свободную урну). Найдите вероятность того, что шар, вынутый из третьей урны, окажется белым.

8.6 В квартире шесть лампочек. Для каждой из них вероятность того, что она останется исправной в течение года, равна 5/6. Какова вероятность того, что в течение года придётся заменить не менее половины лампочек, если они перегорают независимо друг от друга?

8.7 Имеется пять ключей, из которых только один подходит к замку. Составить закон распределения случайной величины Х – число попыток до первого открывания замка, найти М [ Х ]; D [ Х ].

8.8 Пусть случайная величина Х имеет плотность распределения f (x):

Найти параметр с, функцию распределения случайной величины Х, построить график функции распределения.

Вариант 9

9.1 Двое участвуют в розыгрыше лотереи. Пусть событие А – первый участник выиграл более 1000 рублей, событие В – второй выиграл 500 рублей. В чем заключается событие ?

9.2 В классе обучаются 42 ученика. Из них 16 занимаются в секции легкой атлетики, 24 – в футбольной секции, 15 – в шахматной, 11 – в секции по легкой атлетике и в футбольной, 8 – в легкоатлетической и в шахматной, а 6 – во всех трех секциях. Остальные школьники увлекаются только туризмом. Сколько школьников являются туристами?

9.3 Некоторое электронное устройство выходит из строя, если откажет определенная микросхема. Вероятность ее отказа в течение 1 ч работы устройства равна 0,004. Какова вероятность того, что за 100 ч работы придется пять раз менять микросхему?

9.4 Группа из 20 студентов, среди которых 7 хорошистов и 5 отличников, сдаёт экзамен. Хорошист может с равной вероятностью получить «4» или «5», отличник обязательно получит «5», остальные студенты не могут получить «5». Наугад выбранный студент получил «5». Какова вероятность, что он хорошист?

9.5 В ящике 10 деталей, из которых 4 окрашенных. Сборщик наудачу взял 3 детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.

9.6 Десять раз подбрасывается пара игральных костей. Какова вероятность того, что сумма очков, равная 11, выпадет ровно пять раз?

9.7 Две лампочки включают по три раза. Первая при включении перегорает с вероятностью 0,3, вторая – с вероятностью 0,2. Рассматриваются случайные величины Х ₁ и Х ₂ – номера включения соответственно первой и второй лампочек, при которых они перегорели. Найти функцию распределения случайной величины ; построить её график; найти М [ Y ]; D [ Y ].

9.8 Пусть случайная величина Х имеет плотность распределения f (x):

Найти параметр с, функцию распределения случайной величины Х, построить график функции распределения.

Вариант 10

10.1 Известно, что в некотором опыте события А и С произошли, а событие B не произошло. Определите, произошло или нет событие .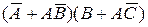

10.2 Сколько раз надо бросить игральную кость, чтобы с вероятностью не меньшей 0,99 утверждать, что «шестерка» выпала не менее 1 раза?

10.3 Электричка состоит из 12 вагонов. Каждый из семи пассажиров наудачу выбирает любой вагон. Найти вероятность того, что все пассажиры сядут в первые три вагона.

10.4 В квадрат с вершинами в точках (0;0), (0;1), (1;1), (1;0) наудачу брошена точка. Найдите вероятность того, что координаты этой точки удовлетворяют неравенству .

10.5 В фирме 60% сотрудников – мужчины, 40% - женщины. Вероятность опоздать на работу для мужчины равна 0,1, для женщины – 0,25. Выбранный накануне наугад из списка сотрудник опоздал на работу. С какой вероятностью это мужчина?

10.6 Стрелок выстрелил 6 раз. Вероятность промаха при каждом выстреле равна 0,3. Найти вероятность того, что стрелок попадёт не менее четырёх раз.

10.7 Две монеты подбрасывают по три раза. На первой монете герб выпадает с вероятностью 0,6, на второй – с вероятностью 0,5. Рассматриваются случайные величины: Х ₁ и Х ₂ – номера подбрасывания соответственно первой и второй монет, при которых выпадет герб. Построить график функции распределения случайной величины ; найти М [ Y ]; D [ Y ].

10.8 Пусть случайная величина Х имеет плотность распределения f (x):

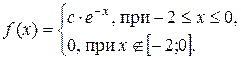
Найти параметр с, функцию распределения случайной величины Х, построить график функции распределения.