1. Находим область определения функции.
2. Вычисляем производную функции.
3. Определяем критические точки.
4. Область определения функции разбиваем критическими точками на промежутки и определяем знак производной на каждом полученном промежутке (с помощью метода интервалов).
5. Делаем выводы о наличие точек экстремума.
6. Вычисляем сами экстремумы функции, т.е. значения функции в точках экстремума.
Замечание. Отметим, что пункты 1-4 совпадают с порядком исследования функции на возрастание и убывание. Поэтому, исследование функции на возрастание-убывание и экстремумы рекомендуется выполнять для функции одновременно.
Теорема (второе достаточное условие экстремума). Пусть функция 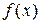 имеет в точке
имеет в точке  и её окрестности непрерывные первую и вторую производные, причём
и её окрестности непрерывные первую и вторую производные, причём 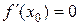 ,
, 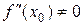 . Тогда функция
. Тогда функция 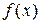 имеет в точке
имеет в точке  минимум (максимум), если
минимум (максимум), если 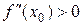
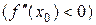 .
.
Доказательство. Пусть 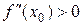 . Так как
. Так как 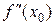 непрерывна в точке
непрерывна в точке  , то
, то 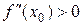 и в некоторой окрестности точки
и в некоторой окрестности точки  . В этой окрестности точки
. В этой окрестности точки  функция
функция 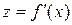 возрастает, так как
возрастает, так как 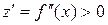 . Но
. Но 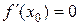 . Следовательно, при переходе через точку
. Следовательно, при переходе через точку  в направлении возрастания
в направлении возрастания 
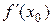 меняет знак с «-» на «+», поэтому
меняет знак с «-» на «+», поэтому 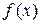 имеет в точке
имеет в точке  минимум.
минимум.
Доказательство в случае  аналогично.
аналогично.
Замечание. Второе достаточное условие имеет более узкую область применения, так как часто при 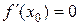 и
и 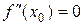 .
.
Для сформулированного достаточного условия экстремума выделим
Порядок исследования функции на экстремум.
1. Находим область определения функции.
2. Вычисляем первую и вторую производные функции.
3. Определяем критические точки.
4. Вычисляем значения второй производной в критических точках
5. Делаем выводы о наличие точек экстремума.
6. Вычисляем сами экстремумы функции, т.е. значения функции в точках экстремума.
10.5
График функции 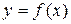 называется выпуклым (вогнутым) на интервале
называется выпуклым (вогнутым) на интервале 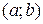 , если соответствующий участок кривой
, если соответствующий участок кривой 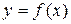 расположен ниже (выше) касательной, проведённой в любой точке
расположен ниже (выше) касательной, проведённой в любой точке 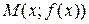 этого графика (Рисунок 10.1).
этого графика (Рисунок 10.1).
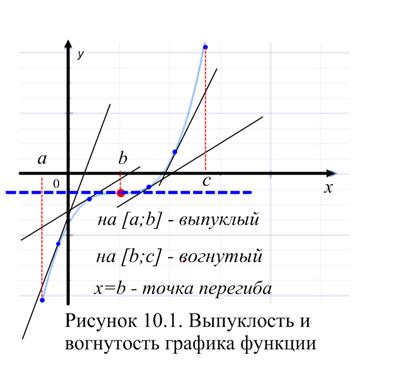
Точка графика дифференцируемой функции 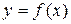 называется точкой перегиба, если при переходе через эту точку график меняет выпуклость на вогнутость или наоборот.
называется точкой перегиба, если при переходе через эту точку график меняет выпуклость на вогнутость или наоборот.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой – над нею.
Теорема (достаточное условие выпуклости и вогнутости функции). Если во всех точках интервала 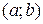 вторая производная функции
вторая производная функции 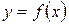 отрицательна, то есть
отрицательна, то есть 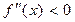 , то кривая на этом интервале выпуклая; если
, то кривая на этом интервале выпуклая; если 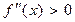 , то кривая на этом интервале вогнутая.
, то кривая на этом интервале вогнутая.
Доказательство. Возьмем в интервале 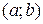 произвольную точку
произвольную точку 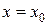 и проведем в этой точке касательную. Пусть уравнение кривой
и проведем в этой точке касательную. Пусть уравнение кривой
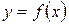 , (10.3)
, (10.3)
уравнение касательной
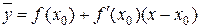 . (10.4)
. (10.4)
Из (10.3) и (10.4) следует 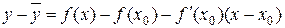 . Применяя теорему Лагранжа к разности
. Применяя теорему Лагранжа к разности 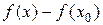 , получим
, получим 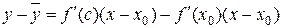 , где
, где 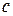 лежит между
лежит между  и
и  , или
, или
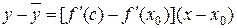 .
.
Применяя теорему Лагранжа к разности 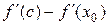 , получаем
, получаем
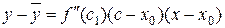 , (10.5)
, (10.5)
где 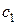 лежит между
лежит между  и
и 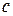 .
.
Если 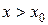 , тогда
, тогда 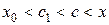 . Так как
. Так как 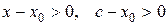 и по условию
и по условию 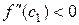 , то
, то 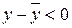 .
.
Если 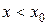 , тогда
, тогда 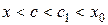 . Так как
. Так как 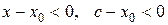 и по условию
и по условию 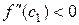 , тогда из (10.5) следует
, тогда из (10.5) следует 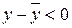 .
.
Таким образом, доказали, что любая точка кривой лежит ниже касательной для любых  и
и  из
из 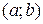 , то есть кривая выпукла.
, то есть кривая выпукла.
Аналогично доказывается вторая часть теоремы.
Теорема (достаточное условие существования точек перегиба). Пусть кривая определяется уравнением 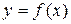 . Если
. Если 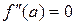 или
или 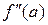 не существует и при переходе через значение
не существует и при переходе через значение 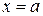 производная
производная 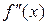 меняет знак, то точка кривой с абсциссой
меняет знак, то точка кривой с абсциссой 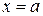 есть точка перегиба.
есть точка перегиба.
Замечание. Внутренние точки области определения функции, в которых 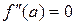 или
или 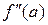 не существует называют критическими точками второго рода.
не существует называют критическими точками второго рода.
Доказательство. Пусть 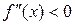 при
при 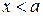 и
и  при
при 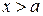 . Тогда при
. Тогда при 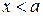 кривая выпукла, а при
кривая выпукла, а при 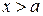 - вогнута. Следовательно, точка кривой с абсциссой
- вогнута. Следовательно, точка кривой с абсциссой 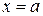 есть точка перегиба.
есть точка перегиба.
Пусть  при
при 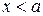 и
и 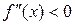 при
при 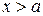 , то при
, то при 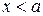 кривая вогнута, при
кривая вогнута, при 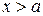 кривая выпукла, то есть точка кривой с абсциссой
кривая выпукла, то есть точка кривой с абсциссой 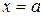 - точка перегиба.
- точка перегиба.
Рассмотренные теоремы в этом пункте позволяют сформулировать