ГИДРОМЕХАНИКА
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________
Краткая теория и методические указания
Во многих задачах гидромеханики используется приближение идеальной жидкости, т. е. абсолютно невязкой и абсолютно несжимаемой.
В задачах, связанных с определением гидростатического давления, используется закон Паскаля и следствия из него. Сделав схематический чертеж, нужно изобразить на нем уровни, занимаемые жидкостью по условию задачи. Поверхность нулевого уровня выбирается так, чтобы она проходила по самой нижней границе раздела сред. Затем на основании следствия из закона Паскаля составляют уравнение равновесия жидкости. Если по условию задачи происходит переливание жидкости из одной части сосуда в другую, то к данному уравнению можно добавить условие несжимаемости жидкости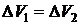 
, где 
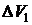и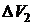 
– соответственно уменьшение объема жидкости в одной части сосуда и увеличение его в другой части. Затем составленную систему уравнений решают относительно искомой величины.
Задачи на равновесие тел в жидкости или газе решают по такому же плану, как и задачи на статику с учетом силы Архимеда.
Если по условию задачи тело движется с постоянным ускорением в жидкости или газе, нужно составить уравнение движения на основании второго закона Ньютона и решать как задачу по динамики.
Стационарным называется такое течение жидкости, при котором в любом сечении выделенного объема скорость жидкости остается постоянной. Для стационарного движения идеальной жидкости имеет место уравнение Бернулли: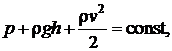 
где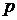 
– статическое давление; 
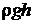– гидростатическое давление; 
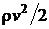– динамическое давление. Из уравнения Бернулли следует, что скорость вытекания жидкости из малого отверстия равна 
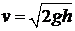, где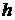 
– высота поверхности жидкости над отверстием (формула Торричелли). Так как через любое поперечное сечение трубы проходят равные объемы жидкости, то 
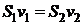, где 
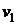и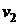 
– скорости жидкости в двух сечениях трубы площадью поперечного сечения 
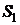и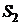 
. Данное выражение называется уравнением неразрывности для несжимаемой жидкости.
Всем реальным жидкостям и газам присуще внутреннее трение (вязкость). Сила трения между слоями вязкой жидкости определяется законом Ньютона, и модуль этой силы определяется площадью соприкосновения двух соседних слоев S с различной скоростью, градиентом скорости движения жидкости в направлении, нормальном к течению (вдоль радиуса)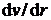 
и коэффициентом пропорциональности, называемой динамической вязкостью жидкости 
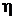. Скорость частиц жидкости изменяется от нуля вблизи стенок трубы до максимума на ее оси. Жидкость при этом оказывается как бы разделенной на тонкие цилиндрические слои, которые скользят относительно друг друга не перемешиваясь. Такое течение называется ламинарным. В этом случае закон изменения скорости вдоль радиуса 
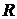трубы имеет вид 
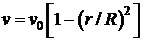, где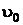 
– скорость жидкости на оси трубы при 
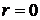; r – текущее расстояние вдоль радиуса (
).
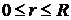Объемный расход жидкости при ламинарном течении в цилиндрической трубе радиусом R определяется формулой Пуазейля.
Два физических процесса называются подобными, если они подчиняются одним и тем же физическим законам. При этом величины, характеризующие подобные явления, получаются путем умножения их на так называемые числа подобия – безразмерные величины, одинаковые для всех однородных величин. В частности, характер течения жидкости определяется значением безразмерной величины, носящей название числа Рейнольдса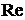 
. Число 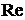характеризует соотношение между силами трения и давления. При малых значениях числа 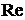течение носит ламинарный характер. Начиная с некоторого значения, называемого критическим, течение приобретает турбулентный характер.
При определении сил, действующих на тело в потоке жидкости или газа, число также служит критерием подобия. Так, при небольших значениях числа 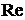, когда сопротивление жидкости или газа обусловлено только силами трения, модуль силы сопротивления среды движению тела описывается формулой Стокса, линейно зависящей от скорости тела.