Скалярная физическая величина, равная отношению модуля силы F,
действующей перпендикулярно поверхности, к площади S этой поверхности, называется давлением:
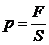 .
.
Гидростатическое давление внутри жидкости на глубине h
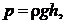
где 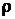 – плотность жидкости.
– плотность жидкости.
Полное давление внутри покоящейся жидкости на глубине h
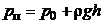 ,
,
где 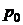 – атмосферное давление.
– атмосферное давление.
Уравнения гидростатики Эйлера
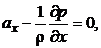
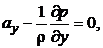
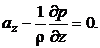
где 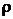 – плотность жидкости,
– плотность жидкости, 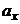 ,
, 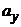 ,
, 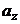 – ускорения, которые способны сообщить массовые силы.
– ускорения, которые способны сообщить массовые силы.
Закон Паскаля
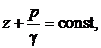
где 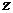 – геометрическая высота,
– геометрическая высота, 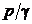 – пьзометрическая высота,
– пьзометрическая высота, 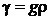 –удельный вес жидкости.
–удельный вес жидкости.
В сообщающихся сосудах с двумя жидкостями, имеющими разную плотность, высоты столбов жидкостей над уровнем из раздела обратно пропорциональны их удельным весам
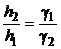 .
.
Сила Архимеда, приложенная к центру масс вытесненной телом жидкости (или газа) и направленная по нормали к открытой поверхности жидкости
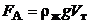 ,
,
где 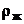 – плотность жидкости,
– плотность жидкости, 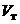 – объем погруженной в эту жидкость часть тела.
– объем погруженной в эту жидкость часть тела.
Уравнение Бернулли
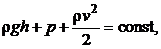
где r – плотность жидкости, v – скорость движения жидкости в данном
сечении трубы, h – высота данного сечения трубы над некоторым уровнем, p – давление.
Формула Торричелли
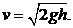
Сила вязкого трения– формула Ньютона
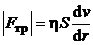 ,
,
где 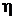 – коэффициент трения жидкости или газа (динамическая вязкость),
– коэффициент трения жидкости или газа (динамическая вязкость), 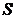 – площадь взаимодействующих слоев,
– площадь взаимодействующих слоев, 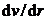 – градиент скорости в направлении, перпендикулярном направлению движения жидкости.
– градиент скорости в направлении, перпендикулярном направлению движения жидкости.
Формула Стокса
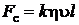 ,
,
где 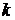 – коэффициент пропорциональности, определяемый формой тела;
– коэффициент пропорциональности, определяемый формой тела; 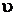 – скорость движения тела в жидкости;
– скорость движения тела в жидкости; 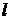 – характерный размер тела.
– характерный размер тела.
Для движения тела в форме шара 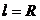 (радиус шара),
(радиус шара), 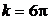 , формула Стокса принимает вид:
, формула Стокса принимает вид:
 ,
,
где 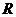 – радиус шарика,
– радиус шарика, 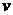 – скорость шарика.
– скорость шарика.
При ламинарном движении объем жидкости (газа), протекающий за время 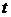 через капиллярную трубку радиусом
через капиллярную трубку радиусом 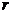 и длиной
и длиной 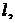 определяется формулой Пуазейля
определяется формулой Пуазейля
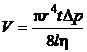 ,
,
где 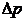 – разность давлений на концах трубки.
– разность давлений на концах трубки.
Характер движения жидкости (газа) определяется безразмерным числом Рейнольдса
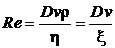 ,
,
где 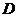 – величина, характеризующая линейные размеры тела, обтекаемого жидкостью (газом),
– величина, характеризующая линейные размеры тела, обтекаемого жидкостью (газом), 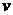 – скорость течения. Отношение
– скорость течения. Отношение 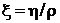 называется кинематической вязкостью.
называется кинематической вязкостью.
Контрольные вопросы
1. В сообщающихся сосудах находится вода. Затем в один из них помещают кусок дерева. Станут ли различаться при этом уровни воды в сосудах?
2. На чашках равноплечих весов стоят два одинаковых стакана, до краев наполненные водой. В одном стакане плавает кусок пенопласта, а в другом – кусок дерева. Будут ли уравновешены весы?
3. Кусок льда, содержащий пузырек воздуха, плавает в стакане с водой. Изменится ли уровень воды в стакане, если лед растает?
4. Кусок льда, содержащий свинцовую пулю, плавает в стакане с водой. Изменится ли уровень воды в стакане, если лед растает?
5. К равноплечим весам подвешены алюминиевый и медный грузы, имеющие одинаковые массы. Нарушится ли равновесие весов, если грузы полностью погрузить в воду?
6. Медная кружка плавает в сосуде с водой. Изменится ли уровень воды в сосуде, если кружка опрокинется и утонет?
7. В сосуде с водой плавает шарик, наполовину погруженный в воду. Какое ускорение необходимо сообщить сосуду, чтобы шарик полностью погрузить в воду?
8. В сосуд с водой одновременно опускаются медный и алюминиевый шарики одинаковой массы. Какой из них упадет на дно раньше?
9. Сформулируйте уравнение неразрывности.
10. Показать, что при установившемся течении идеальной жидкости для любой трубки тока выполняется соотношение 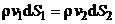 , где
, где 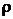 – плотность жидкости,
– плотность жидкости, 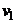 и
и 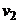 - скорости жидкости в торцевых сечениях трубки, площади которых
- скорости жидкости в торцевых сечениях трубки, площади которых 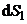 и
и 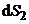 соответственно.
соответственно.
11. Запишите уравнение Бернулли.
12. Какую силу сопротивления испытывает падающий в вязкой жидкости или газе шарик?
13. Для какого движения справедлив закон Стокса?
14. Выведите формулу Торричелли.
Примеры решения задач
Задача 1
Шар диаметром 1 м плавает в воде (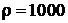 кг/м3), погрузившись в нее на 20 см. Найти минимальную работу, которую надо совершить, чтобы погрузить шар в воду до диаметральной линии.
кг/м3), погрузившись в нее на 20 см. Найти минимальную работу, которую надо совершить, чтобы погрузить шар в воду до диаметральной линии.
Решение.
В качестве исходного (нулевого) положения шара примем его равновесное положение 1 (рис. 5.1), когда он погружен на глубину h, а сила Архимеда 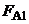 уравновешена силой тяжести
уравновешена силой тяжести 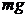 . При погружении шара до диаметральной линии внешняя сила совершает работу против
. При погружении шара до диаметральной линии внешняя сила совершает работу против
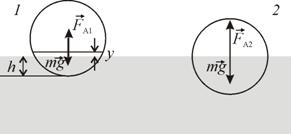 Рис. 5.1
Рис. 5.1
| возрастающей силы Архимеда на пути в пределах от  до до  . Сила тяжести будет способствовать погружению. Поэтому искомая работа будет равна . Сила тяжести будет способствовать погружению. Поэтому искомая работа будет равна
|
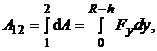 (5.1)
(5.1)
где 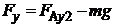 – выталкивающая сила при погружении шара от первоначального положения (глубина
– выталкивающая сила при погружении шара от первоначального положения (глубина 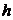 ) до глубины
) до глубины 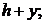
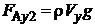 – сила Архимеда при погружении шара до глубины
– сила Архимеда при погружении шара до глубины 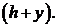
Объем 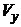 погруженной части шара будет равен объему шарового сегмента высотой
погруженной части шара будет равен объему шарового сегмента высотой 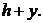 Тогда в соответствии с рисунком запишем:
Тогда в соответствии с рисунком запишем:
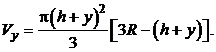
Силу тяжести mg определим из условия равновесия шара в воде до начала погружения:
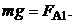
Поскольку 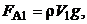 то сила тяжести шара будет равна:
то сила тяжести шара будет равна:
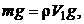
где 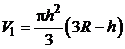 – объем погруженного в воду шарового сегмента высотой
– объем погруженного в воду шарового сегмента высотой 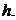
С учетом сказанного, выталкивающая сила при погружении шара до глубины 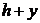 будет равна:
будет равна:
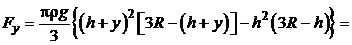
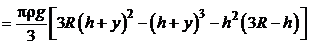 .
.
Следовательно, искомая работа 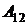 в соответствии с выражением (5.1) будет равна:
в соответствии с выражением (5.1) будет равна:
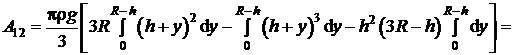
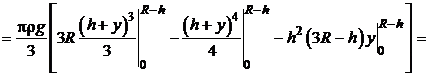
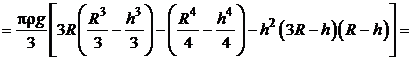
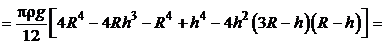
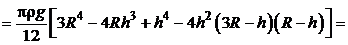
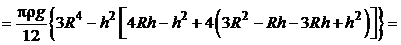
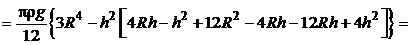
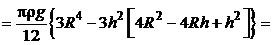
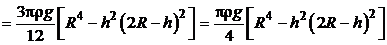 .
.
Подставляем численные данные из условия задачи:
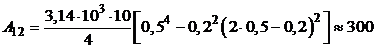 Дж.
Дж.
Ответ: 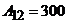 Дж.
Дж.
Задача 2
Из брандспойта с выходным сечением 1,0 см2 бьет вертикально вверх струя жидкости, расход которой составляет 1,0 л/с. Найти площадь поперечного сечения струи на высоте 3,2 м над концом брандспойта.
Решение.
Объемный расход жидкости для первого и второго сечения с учетом уравнения неразрывности
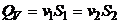 , (5.2)
, (5.2)
откуда искомая площадь
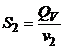 . (5.3)
. (5.3)
Скорость во втором сечении определим из уравнения Бернулли. Считая, что атмосферное давление у выходного отверстия брандспойта и на высоте h одинаково (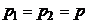 ), для первого и второго сечений запишем:
), для первого и второго сечений запишем:
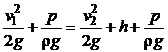 ,
,
откуда
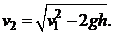
Тогда, подставляя полученное выражение в формулу искомой величины (5.3) с учетом 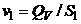 (согласно (5.2)), получаем
(согласно (5.2)), получаем
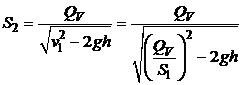 .
.
Подставляем численные данные из условия задачи:
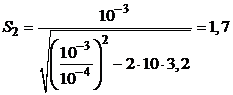 см2.
см2.
Ответ:  = 1,7 см2.
= 1,7 см2.
Задача 3
Если в бак цилиндрической формы с площадью основания 20 м2 и объемом 400 м3 налита жидкость и он имеет в дне отверстие площадью 9,2 × 10–4 м2, Найти время, необходимое для полного опустошения бака.
Решение.
Очевидно, что скорость вытекания воды в отверстие 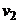 будет умень-
будет умень-
шаться по мере падения уровня воды в баке. По этой причине объемный расход 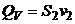 также будет величиной изменяющейся. Выделим элемент толщиной также будет величиной изменяющейся. Выделим элемент толщиной 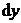 , находящийся на высоте y от дна бака и имеющий объем , находящийся на высоте y от дна бака и имеющий объем 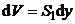 (рис. 5.2). Тогда время опустошения бака найдем как интеграл (рис. 5.2). Тогда время опустошения бака найдем как интеграл 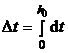 , где , где 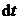 – время опустошения объема – время опустошения объема 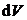 , находящегося на высоте y от дна бака. Объемный расход, с одной стороны, равен , находящегося на высоте y от дна бака. Объемный расход, с одной стороны, равен 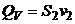 , а с другой стороны, , а с другой стороны, 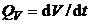 . Скорость . Скорость 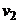
| 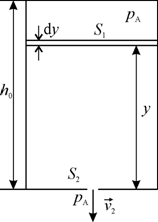 Рис. 5.2
Рис. 5.2
|
определим, пользуясь уравнением Бернулли для сечений 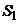 и
и  :
:
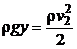 ,
,
откуда интересующая нас скорость
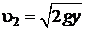 .
.
Тогда, приравнивая выражения для расхода, можем записать:
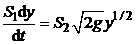 ,
,
откуда
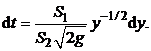
Подставляя это выражение в формулу искомой величины, получаем
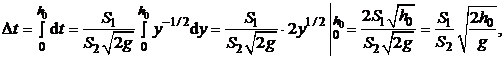
или, с учетом того, что 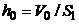 , запишем окончательное выражение искомой величины в следующем виде:
, запишем окончательное выражение искомой величины в следующем виде:
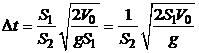 .
.
Подставляем численные данные:
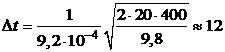 часов.
часов.
Ответ: 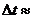 12 часов.
12 часов.
Задача 4
Дождевая капля диаметром 0,6 мм (r1 = 1000 кг/м3) падает в воздухе (r2 = 1,3 кг/м3, h = 10–5Па × с). Найти наибольшую скорость, которая она может достичь.
Решение.
При начале падения капли под действием силы тяжести 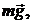 направленной вниз, по мере увеличения ее скорости
направленной вниз, по мере увеличения ее скорости 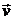 , возрастает сила сопротивления движению капли в воздухе
, возрастает сила сопротивления движению капли в воздухе 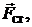 направленной вверх. Соответственно, уменьшается ускорение капли, но ее скорость продолжает увеличиваться, а значит и сила
направленной вверх. Соответственно, уменьшается ускорение капли, но ее скорость продолжает увеличиваться, а значит и сила 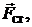 до тех пор, пока сумма
до тех пор, пока сумма 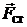 и силы Архимеда
и силы Архимеда 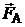 не станет равной
не станет равной 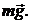 . В этот момент ускорение капли становится равной нулю, а скорость становится постоянной. В проекциях на ось OY можно записать:
. В этот момент ускорение капли становится равной нулю, а скорость становится постоянной. В проекциях на ось OY можно записать:
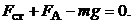 (5.4)
(5.4)
При выполнении условия (5.4) скорость капли будет максимальной.
Модуль силы сопротивления в соответствии с формулой Стокса для шара радиусом R имеет вид:
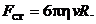 (5.5)
(5.5)
Модуль силы Архимеда записывается следующим образом:
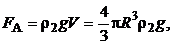 (5.6)
(5.6)
где 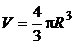 – объем капли в виде шара.
– объем капли в виде шара.
Наконец, модуль силы тяжести
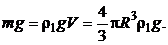 (5.7)
(5.7)
Подставляя выражения (5.5)–(5.7) в уравнение (5.4), получаем:
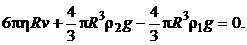
Проведя необходимые преобразования, запишем:
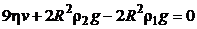 ,
,
Откуда выражение для искомой скорости примет вид: 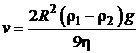 »20 м/с.
»20 м/с.
Ответ: 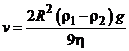 »20 м/с.
»20 м/с.
Задача 5
В дне цилиндрического сосуда диаметром 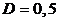 м имеется круглое отверстие диаметром м имеется круглое отверстие диаметром 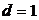 см (рис. 5.3). Найти зависимость скорости понижения уровня воды в сосуде от высоты см (рис. 5.3). Найти зависимость скорости понижения уровня воды в сосуде от высоты 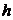 этого уровня. Найти значение этой скорости для высоты этого уровня. Найти значение этой скорости для высоты 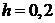 м. Воду считать идеальной несжимаемой жидкостью. м. Воду считать идеальной несжимаемой жидкостью.
| 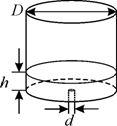 Рис. 5.3
Рис. 5.3
|
Решение.
Площадь поперечного сечения сосуда 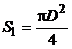 . Скорость понижения воды в сосуде – это скорость течения жидкости
. Скорость понижения воды в сосуде – это скорость течения жидкости  в сечении
в сечении 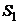 . Площадь поперечного сечения отверстия
. Площадь поперечного сечения отверстия 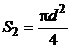 . Скорость вытекания воды из отверстия – это скорость течения жидкости
. Скорость вытекания воды из отверстия – это скорость течения жидкости 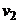 в сечении
в сечении 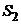 . Согласно уравнению Бернулли:
. Согласно уравнению Бернулли:
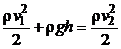 .
.
Так как плотность воды постоянна, что следует из условия о ее несжимаемости, уравнение Бернулли можно переписать:
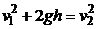 .
.
Используем уравнение неразрывности струи жидкости:
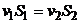 .
.
Отсюда найдем зависимость 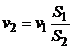 . Подставим данное выражение в уравнение Бернулли и получим:
. Подставим данное выражение в уравнение Бернулли и получим:
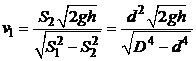 .
.
Так как 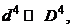 то приближенно
то приближенно 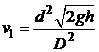 . Отметим, что если
. Отметим, что если 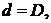 то
то 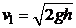 . При
. При 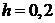 м скорость
м скорость 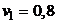 мм/с.
мм/с.
Ответ: 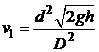 ,
, 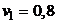 мм/с.
мм/с.
Задача 6
По трубе длиной 10 м течет вязкая жидкость (h = 10–3 Па × с) со скоростью 2 м/с вдоль оси потока. Найти силу трения, которую испытывает труба со стороны жидкости.
Решение.
Сила трения, которую испытывает труба со стороны жидкости, в соответствии с законом Ньютона будет равна:
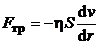 , (5.8)
, (5.8)
где 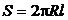 – площадь стенки трубы;
– площадь стенки трубы; 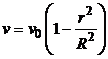 – зависимость изменения скорости вдоль радиуса трубы,
– зависимость изменения скорости вдоль радиуса трубы, 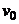 – скорость жидкости на оси трубы при r = 0, R – радиус трубы, произвольное расстояние вдоль радиуса (
– скорость жидкости на оси трубы при r = 0, R – радиус трубы, произвольное расстояние вдоль радиуса (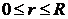 ).
).
Определим значение градиента скорости жидкости на стенке трубы (при r = R):
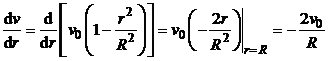 .
.
Подставим полученные выражения площади S и градиента d v /d r в выражение (5.8) искомой величины:
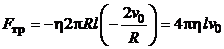 =0,25 Н.
=0,25 Н.
Ответ: 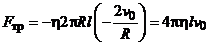 =0,25 Н.
=0,25 Н.
Задача 7
В боковую поверхность сосуда, стоящего на столе, вставлен горизонтальный капилляр с внутренним радиусом 1 мм и длиной 4,5 см на высоте 80 см от дна сосуда, а в сосуд налито машинное масло (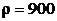 кг/м3,
кг/м3, 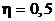 Па × с), уровень которого поддерживается постоянным на высоте 1 м выше капилляра. Найти расстояние по горизонтали, на которое улетает струя масла от сосуда.
Па × с), уровень которого поддерживается постоянным на высоте 1 м выше капилляра. Найти расстояние по горизонтали, на которое улетает струя масла от сосуда.
Решение.
Так как при неизменном уровне h 1 масла над капилляром, модуль скорости 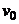 вытекания струи из капилляра будет неизменным, а направление ее горизонтальным, то искомое расстояние равно: вытекания струи из капилляра будет неизменным, а направление ее горизонтальным, то искомое расстояние равно:
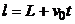 , (5.9)
где , (5.9)
где 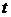 – время полета струи от конца – время полета струи от конца
| 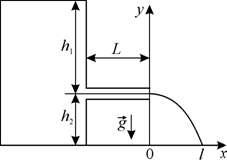 Рис. 5.4
Рис. 5.4
|
капилляра до горизонтальной поверхности.
Вдоль вертикальной оси 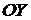 струя проходит пуль
струя проходит пуль 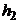 под действием ускорения свободного падения
под действием ускорения свободного падения 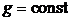 без начальной скорости (т. к. скорость
без начальной скорости (т. к. скорость 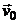 направлена горизонтально, то вертикальная ее составляющая равна нулю). Следовательно, указанный путь будет равен:
направлена горизонтально, то вертикальная ее составляющая равна нулю). Следовательно, указанный путь будет равен:
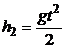 ,
,
Откуда время полета:
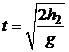 . (5.10)
. (5.10)
Модуль скорости вытекания масла из капилляра 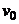 определим из следующих соображений. По уровню неразрывности объемный расход
определим из следующих соображений. По уровню неразрывности объемный расход
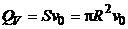 .
.
С другой стороны, в соответствии с формулой Пуазейля, объемный расход вязкой жидкости, протекающей через капиллярную трубку
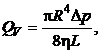
где 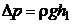 – гидравлическое давление масла над капилляром.
– гидравлическое давление масла над капилляром.
Приравнивая выражения для расхода, получаем
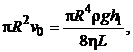
откуда скорость
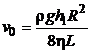 . (5.11)
. (5.11)
Подставив выражение (5.10) и (5.11) в искомую величину (5.9), получим
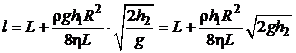 = 6,5 см.
= 6,5 см.
Ответ: 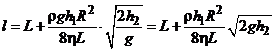 = 6,5 см.
= 6,5 см.
Задача 8
Железный шарик (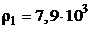 кг/м3) диаметром 5,0 мм падает в касторовом масле (
кг/м3) диаметром 5,0 мм падает в касторовом масле (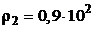 кг/м3, h = 1,0 Па × с). Найти число Рейнольдса при установившемся движении шарика.
кг/м3, h = 1,0 Па × с). Найти число Рейнольдса при установившемся движении шарика.
Решение.
Формула для числа Рейнольдса имеет вид
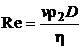 , (5.12)
, (5.12)
где 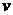 – установившаяся скорость движения шарика;
– установившаяся скорость движения шарика; 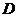 – его диаметр.
– его диаметр.
Скорость движения шарика станет установившейся, когда сила тяжести будет уравновешена суммой силы сопротивления движения Стокса и силой Архимеда. В этом случае ускорение шарика будет равно
нулю. В проекции на ось 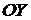 можно записать:
можно записать:
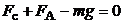 . (5.13)
. (5.13)
Формула для силы Стокса имеет вид:
 . (5.14)
. (5.14)
Модуль силы Архимеда записывается следующим образом:
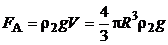 , (5.15)
, (5.15)
где 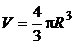 – объем капли в виде шара.
– объем капли в виде шара.
Наконец, модуль силы тяжести
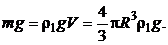 (5.16)
(5.16)
Подставляя выражения (5.14)–(5.16) в уравнение (5.13), получаем:
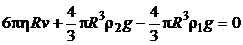 .
.
Проведя необходимые преобразования, запишем:
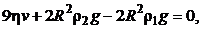
откуда выражение для искомой скорости примет вид
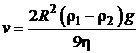
Подставив выражение скорости в выражение (5.12), получим
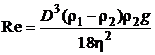 = 0,44.
= 0,44.
Ответ: 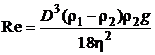 = 0,44.
= 0,44.