Различные виды измерениий иеют разные предельные распределения. Не все предельные распределения имеютвид симметричного колокола, расмотренного в лекции 5.2. (Например, биномиальное распределение и распределение Пуассона, рассматриваемые в лекции 13 и 14, обычно не симметричны). Тем не менееоказывается, что огромное множество измерений имеет в качестве предельного распределения симметричную колоколообразную кривую.
Действительно, мы покажем в лекции 13, что если на результат измерения оказывает влияние большое число источников небольших случайных ошибок, а систематические ошибки пренебрежимо малы, то измеренные значения
 f(x)
f(x)
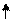

 x
x
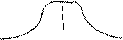
истинное значение
распределяются по колоколообразной кривой, центр которой будет истинным значением х, как показано на рис. 5.7. В оставшиеся части этой главы мы ограничимся рассмотрением измерений только с такими свойствами.
Если наши измерения подвержены заметным систематическим ошибкам, то мы не можем ожидать, что предельное распределение будет иметь центр, совпадающий с истинным значением. Случайные ошибки с равной вероятностью смещают наши отсчеты в обе стороны от истинного значения.Если все ошибки случайны, то после многочисленных измерений будет получено одинаково много результатов, как превышающих истинное значение,так и не достигающих его.
Однако систематическая ошибка (подобно растянутой рулетке или отстающим часам) смещает все значения в одну сторону и, следовательно, смещает центр распределения полученных значений от истинного значения. В данной главе мы будем предполагать, что центр распределения приходится на истинное значение. Это эквивалентно предположению, что все систематические ошибки уменьшены до пренебрежимо малого уровня.
Теперь настало время обратиться к вопросу, который мы до сих пор избегали обсуждать: что такое «истинное значение»физической величины? Это трудный вопрос, на который нет удовлетворительного ростого ответа. Поскольку очевидно, что ни в каком измерений нельзя точно определить истинное значение любой непрерывной переменной (например, длины,времени и т.д.), то не ясно, существует ли вообще истинное значение такой величины. Тем не менее оказывается очень удобным предпологать, что дюбая физическая величина имеет истинное значение, и мы всегда будем исходить из этого предположения.
Истинным значением величины можно считать такое значение, к которому мы приближаемся по мере осуществления
 |
все большего большего числа измерений,выполняемых все более тщательно. Определение таким образом «истинное значение» есть идеализация, аналогичная понятию математической точки, которая не имеет ширины; и по этим двум понятиям, это полезная идеализация.
Мы часто будем обозначать истинные значения измеряемых величин х.у,... соответствующими прописными буквами Х,У,.. Если измерения величины х подвержены множеству небольших слуайных ошибок и если систематические ошибки пренебрежимо малы, то распределение результатов измерений будет иметь вид симметричной колоколообразной кривой с центром, приходящимся на истинное значение Х.
В математике функция, график которой имеет форму колоколообразной ривой, называется функцией Гаусса. Основная форма представления этой функции имеет вид
е-х2/2σ2 (5.17)
где σ – фиксированный параметр, который мы будем назывть параметром ширины или шириной. Читателю полезно ознакомиться со свойствами этой функции.
Когда х = 0, функция Наусса (5.17) равна единице. Функция симметрична относительно х = 0, так и для х, так и для – х. При удалении х от нуля в любом направлении функция х2/2σ2 возрастает, причем возрастает быстро, если величина σмала, и более медленно, если σ велика. Следовательно, по мере удаления х от нуля функция (5.17) стремится к нулю. Таким образом, общий вид функции Гаусса (5.17) будет таким, как показано на рисунке 5.8. Этот график объясняет термин «параметр ширины» для σ, поскольку при больших значениях σ колокол выглядит широким, а при малых σ – узким.
Функция Гаусса (5.17) представляет собой колоколообразную кривую с центром в х = 0. Чтобы получить колоколообразную кривую с центром в какой-то другой точке х=Х. Мы просто заменим х в (5.17) на х-Х.
Таким образом, функция
е-(х-Х)2/2σ2 (5.18)
достигает максимума при х=Х и спадает симметрично по обе стороны от х=Х, как показано на рисунке 5.9.
Выражение (5.18) еще не является окончательным, оно не описывает предельное распределение, поскольку любое распределение должно быть нормировано, т.е. должно удовлетворять условию
∫-∞∞ f(x) dx=1. (5.19)
Чтобы выполнить это условие, мы введем
f(x)=Ne-(x-X)2/2σ2. (5.20)
(Умножение на N не изменяет ни формы, ни положения максимума при х=Х.) Теперь мы должны выбрать «нормировочный множитель» N таким образом, чтобы f(x) была нормирована в соответсвии с (5.19). Для этого необходимо сделать подстановку подынтегрального выражения, которую мы приведе:
∫-∞∞ f(x) dx=∫-∞∞ Ne-(x-X)2/2σ2 dx. (5.21)
 При оценке интегралов такого вида всегда нужно произвести замену переменных, чтобы упростить подынтегральное
При оценке интегралов такого вида всегда нужно произвести замену переменных, чтобы упростить подынтегральное
 1
1

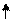

 x
x
х=Х
Рисунок 5.9. Функция Гаусса (5.18) колоколообразной формы с центром в х=Х.
выражение. Обозначим х-Х=у (в этом случае dx=dy) и получим
=N ∫-∞∞ e-у 2/2σ2 dу. (5.22)
Затем мы можем обозначить у/σ=z (в этом случае dy=σ dz), тогда
=Nσ ∫-∞∞ e-z2/2 dz (5.23)
Получившийся интеграл – один изи стандартных интегралов математической физики. Его можно рассчитать элементарными методами, но детали вычислений не особенно интересны, поэтому мы прсото приведем результат
∫-∞∞ e-z2/2 dz=√2π (5.24)
Возвращаясь к (5.21) и (5.23), находим, что
∫-∞∞ f(x) dx=Nσ√2π
Так как этот интеграл должен быть равен единице, нормировочный множитель N следует выбрать как N=1/(σ√2π).
Мы приходим к выводу, что нормированная функция Гаусса, или нормированная функция нормального распределения, имеет вид
| f x, σ(x) = 1/σ√2π e-(x-X)2/2σ2. |
(5.25)
Обратите внимание на то, что мы добавили нижние индексы Х, σ, чтобы указать центр и ширину распределения. Функция f x, σ(x) описывает предельное распределение результатов измерений величины х, истинное значение которой равно Х и на которую оказывают влияние только случайные ошибки. Говорят, что результаты измерений распределены нормально, если их предельное распределение описывается функцией Гаусса (5.25).
Высоко мы выясним значение параметра ширины σ. Однако уже ясно, что малые значения σ приводят к распределению типа острого пика, сответствующего точным измерениям, в то время ка большие значения σ дают широкое распределение, соответсвующее измерениям с малой точностью. На рисунке 5.10 приведены два примера распределения Гаусса с различными центрами Х и ширинами σ.
Обратите внимание, как фактор σ в знаменателе формулы (5.25) автоматически обеспечивает для более узкого распределения (σ меньше) большую высоту в центре, как это и должно быть, чтобы полная площадь под кривой равнялась 1.
Практическое занятие №6:
Пример задание 6.1
6.1. Усердная студентка делает 50 измерений количества теплоты Q, выделяющиеся в определенном процессе. Она получает среднее значение и стандартное отклонение, равные соответственно Q=4,8 и δQ=0,4, где оба результаты выражены в калориях.
а) Предпологая, что результаты ее измерений подчиняются нормальному распределению, найдите вероятность того, что любое единичное измерение приведет к результату, отличающемуся от Q ног 0,8 ккал или более.
Сколько результатов, отличающтхся от Q ног 0,8 ккал ей следует ожидать? Если бы один из результатов ее измерений был равен 4,0 ккал и она решила бы использовать критерий Шовене, то отбросила ли бы она этот результат?
б) Если бы один из ее результатов составлял 6,0 ккал, то отбросила ли бы она его?
Практическое занятие №7
Три студента измеряют сопротивление несколько раз и получают три следующих ответа (в омах):
(значение первого студента для R)=11 ± 1;
(значение второго студента для R)=12 ± 1;
(значение третьего студента для R)=10±3.
Если даны три результата, то какова наилучшая оценка для сопротивления R? Три погрешности δ1,δ2,δ3 равны соответственно1,1и3.Следовательно, соответствующие три веса ω1=1/σ2i равны
ω1=1, ω2=1, ω3=1/9
Таким образом, в соответствии с наилучшая оценка есть
Rнайл= ΣωiRi/Σωi= (1·11)+(1·12)+(1/9·10)/1+1+1/9=11.42 Погрешность этого результата определяется как
σRнайл=(Σωi)-1/2= (1+1+1/9)-1/2=0,69
Таким образом6 наш конечный вывод имеет вид
R= 11,4 ± 0,7 Ом
Интересно проследить, какой-то ответ мы полностью игнорировали результаты измерений третьего студента, которые в три раза менее точны и, следовательно, в девять раз менее важны. В этом случае простое вычисление дает Rнайл=11,50(по сравнению с 11,42) с погрешностью 0,71 (по сравнению с 0,69). Очевидно, третье измерение не имеет большого значения.
Практическое занятие №8
Коэффициент доверия.
Теперь мы можем вернуться к двум вопросам, затронутым впервые в лекци и 2, на которые до сих пор не было дано исчерпывающего ответа. Во-первых, какой смысл мы вкладываем в ставшее уже привычным выражение: «Мы в разумной степени уверен, что некоторая измеренная величина лежит в интервале хнайл±δх»? Или, выражаясь опрелеленнее, как можно дать колличественную характеристику степени нашего доверия к любому экспериментальному результату?
Что касается первого вопроса,то ответ должен быть теперь ясен. Если мы измеряем величину х несколько раз (как это обычно бывает), то наша наилучшая оценка для х сеть среднее х, а его стандартное отклонение σх есть наша наилучшая оценка погрешности среднего.
Мы могли бы сделать вывод, что
(значение х)=х± σх,
подразумевая под этим, что согласно нашим наблюдениям можно ожидать, что в 68% случаев результаты любых последующих измерений х, сделанных с той же тщательностью, попадут в интервал х ± σх.
Нашу погрешность можно оценить иначе. Например, мы могли бы предпочесть такую характеристику:
(значение х)= х± 2σх
В этом случае указывался бы интервал, в котором, как мы ожидаем, будет лежать 95% результатов всех однотипных измерений. Ясно, что при представлении любого измеренного значения главное – привести интервал (или погрешность измерения) и коэффициент доверия, сответствующий этому интервалу. Наиболее часто приводится стандартное отклонение результата, которое понимается как 68%-ный доверительный предел, т. е. коэффициент доверия в этом случае равен 68%.
Как подчеркивалось в лекции 2, почти все экспериментальные заключения содержат сравнение двух или более чисел. Воружившись статистической теорией, мы теперь можем дать колличественные критерии для многих таких сравнений. Сейчас мы рассмотрим тоьлко один тип эксперимента, в котором получают некоторое число и сравнивают полученный результат с известным ожидаемым ответом. Заметьте, что под этот частный случай попадают многие интересные эксперименты. Например, в экперименте по проверке закона сохранения импульса мы могли бы измерить начальный и конечный импулься р и р', чтобы проверить, что р=р' (в пределах погрешностей), но мы можем в равной мере считать, что ищется значение (р-р'), которое срванивается с ожидаемым ответом, равным нулю.
В общем случае, огда мы хотим сравнить результаты любых двух измерений, в котором измеряется величина (подобная g, ускорению свободного падения), для которой известно точное принятое значение, также попадает под этот тип экспериментов, причем ожидаемым результатом является известное принятое значение.
Предположим, что студент измеряет некоторую величину х (подобную равности двух импульсов, которые предположительно равны) в виде
(значение х)= хнайл±σ,
где σ обозначает стандартное отклонение его результата.(Это будет стандартное отклонение среднего, если хнайл есть среднее нескольких измерений). Пусть затем он сравнивает свой результат с ожидаемым ответом хож.
В лекции 2 мы омечали, что если различие [хнайл- хож] меньше (или только незначительно больше), чем σ, то согласие будет удовлитварительным, но если [хнайл- хож] много больше, чем σ, то оно неудовлитворительно. Сами по себе эти критерии правильны, но не дают никакой количественной характеристики того, насколько хорошо или плохо это согласие. Они также не говорят нам ничего о границах, которые еще допустимы для согласия. Будет ли различие в 1,5σ свидетельствовать об удовлитвоительном согласии? А в 2σ?
Теперь мы сможем ответить на эти вопросы, если предположим, что результаты измерений нашего студента подчиняются нормальному распределению (а это определенно разумно). Предположим две рабочие гипотезы относительно этого распределения:
а)центр распределения совпадает с ожидаемым ответом хож;
б) параметр ширины распределния равен оцененной студентом величине σ.
Гипотеза «а», конечно, заключается в том, что студент при измерении получает правильный ответ.
Практическое занятие №9
Пример.
Студент делает десять измерений одной длины х и получает результаты (все в миллиметрах)
46, 48, 44, 38, 45, 47, 58, 44, 45, 43.
Заметив, что значение 58 кажется аномально большим, он проверяет свои записи, но не находит указаний на то, что результат получился по ошибке. Тогда он примеяет критерий Шовене. Какой вывод он сделает? Учитывая временно все десять измерений, он рассчитывает
х=45,8 и σх = 5,1.
Разность между подозрительным значением хпод=58 и средним х=45,8 равна 12,2, или 2,4 стандартных отлонений, т.е.
хпод-х/ σх=58-45,8/5,1=24
Из таблицы приложения А он находит: вероятность того, что результат будет отличаться от х на 2,4 σх или более, равна
Р (вне 2,4 σ)= 1-Р (в пределах 2,4 σ)= 1-0,984=0,016.
Для десяти измерений он мог бы, следовательно, получить только 0,16 случаев такого плохого измерения, как подозрительный результат. Так как это число меньше '/г, числа, устнавливаемого критерием Шовене, то студент должен по крайней мере рассмотреть возможность отбрасывания этого результата.
Следующий подозрительный результат – 38, который на 1,5 стандартных отклонений отличется от среднего х=45,8.
Аналогичные вычисления показывают, что среди десяти результатов он мог бы ожидать 1,3 случаев таких же плохих результатов, как и этот, так что этот результат вполне приемлем. Если же он решит выбросить подозрительный результат 58, то он должен пересчитать х и ах и получить
44,4 и σх =2,9.
Как можно было ожидаь, среднее изменилось немного, а стантартное отклонение заметно уменьшилось.