Заметим, что построение интерполяционного многочлена Pn (x), единого для всего отрезка [ a, b ], связано с решением системы уравнений (4), что требует при большом числе узлов xi выполнения большого объема вычислительной работы. Поэтому при решении практических задач используются так называемые интерполяционные формулы. К ним относятся формулы Лагранжа, Ньютона, Гаусса, Бесселя др.
Пусть на отрезке [ a, b ] заданы узлы n +1 различных произвольных значений аргумента x: x 0, x 1, x 2 ,…, xn, и известны для функции 
значения 
; 
; 
; … 
.
Необходимо построить полином 
степени не выше n, имеющий в узлах x 0, x 1, x 2 ,…, xn те же значения, что и функция 
, т.е. 
.
Запишем искомый полином в виде
, (6)
в котором множитель 
равен
(7)
имеет степень n и обладает двумя свойствами:
;
.
Эти свойства означают, что, например, множитель 
в узле x 0 равен единице, а в остальных узлах равен нулю, множитель 
в узле x 1 равен единице, а в остальных узлах равен нулю и т. д.
Подставив в формулу (6) значение из (7), получим
. (8)
Легко заметить, что в силу свойств множителя степень многочлена 
не выше n и он удовлетворяет условиям:
.
Многочлен (8) называется интерполяционной формулой Лагранжа. Формула Лагранжа в краткой форме имеет вид
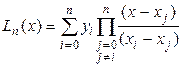. (9)
Пример 1. Заданы значения функции 
в точках: 
, 
; 
, 
; 
, 
; 
, 
.
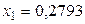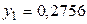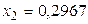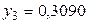Используя многочлен Лагранжа, вычислить значение 
.
Согласно формуле Лагранжа (9), имеем
Подставляя значения xi и yi, после несложных преобразований получим
.
При 
находим 
[3].
Применение интерполяционной формулы Лагранжа при локальной интерполяции. Простейшим и наиболее часто применяемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что на отрезке 
, в точке x которого требуется найти значение функции 
, последняя аппроксимируется линейной функцией. Геометрический смысл такого подхода заключается в замене графика функции , проходящего через заданные точки 
и 
отрезком прямой. Уравнение этой прямой может быть построено, используя положения аналитической геометрии. Однако это уравнение проще получить с помощью интерполяционной формулы Лагранжа.
Например, необходимо построить уравнение для линейной интерполяции (n = 1) некоторой функции в точке x, находящейся на i - м отрезке интервала [ a, b ]. Согласно формуле (9), получим
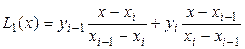. (10)
В случае, когда в ходе решения задачи необходимо многократно вычислять значения некоторой функции для различных значений точки x, принадлежащим двум смежным отрезкам 
и 
интервала [ a, b ], то удобно осуществлять интерполирование с использованием квадратного трехчлена. Такую интерполяцию называют квадратичной или параболической интерполяцией.
Построение квадратного трехчлена выполняют обычно, применяя интерполяционный многочлен Лагранжа (n = 2). Например, для любых заданных трех точек , 
и 
формула (9) примет вид:
(11)
При использовании линейной или квадратичной интерполяции многочлены (10) и (11) приводят к виду 
или 
, где коэффициенты a, b, и c находят, подставив в (10) и (11) известные значения функции и значения соответствующих узлов сетки.
Рассмотренные выше интерполяционные многочлены получены для произвольной сетки узлов на интервале [ a, b ]. В практических задачах значения аппроксимируемой функции часто заданы на равномерной сетке, т.е. для равноотстоящих узлов. В этом случае упрощаются формы интерполяционных многочленов, в частности, формула Лагранжа.
Пусть имеем равномерную сетку узлов интерполирования, на которой шаг h интерполяции 
(рисунок 1). Введем обозначение
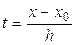. (12)
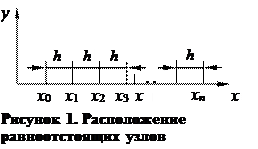Из формулы (12) и рисунка 1 имеем:
;
;
;
…………………………
;
…………………………
.
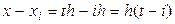Подставив эти соотношения в выражение (7)
для 
, получим
.
Заметим, что в знаменателе полученного выражения для 
, 
. Учитывая это и умножив числитель и знаменатель этого выражения на 
, после преобразований найдем
, где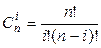 
.
Подставив полученное выражение для 
в интерполяционный многочлен Лагранжа (6), получим
