Согласно условиям задачи интерполирования, построенные для аппроксимируемой функции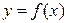 
многочлены 
, 
и 
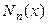принимают значения 
, 
,…, 
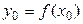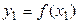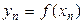, совпадающие со значениями функции 
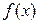только в точках x 0, x 1, x 2 ,…, xn интервала [ a, b ]. Для других значений 
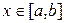значения интерполяционного многочлена, очевидно, будут отличаться от значений 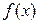на некоторую величину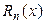 
.
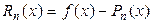Возникает вопрос, какова величина остаточного члена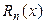 
интерполяционной формулы. Величина остаточного члена 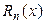зависит от ряда факторов - свойств функции 
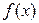, числа и расположения узлов xi, шага h, положения точки x * интерполирования. Поэтому в самом общем случае этот вопрос является открытым и подлежит исследованию для каждого конкретного аппроксимационного процесса.
При определении величины остаточного члена 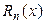, прежде всего, выясняют, что может быть принято за меру погрешности интерполяционной формулы. Если точка x * интерполирования фиксирована, то за меру погрешности принимают величину
,
т. е. отклонение функции 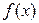от ее интерполяционного многочлена в точке x = x *.
Если точка x * интерполирования заранее неизвестна, а интерполирование осуществляется на всем отрезке [ a, b ], то за меру погрешности принимают максимальное значение абсолютной величины разности между функцией 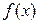и интерполяционным многочленом на отрезке [ a, b ] (рисунок 2)
.
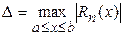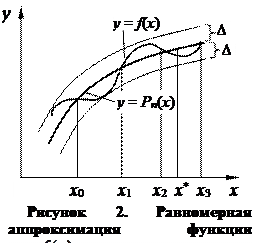В этом случае считается, что многочлен 
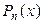равномерно аппроксимирует функцию 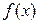с точностью ∆ на отрезке [ a, b ]. При этом величина ∆ называется равномерной оценкой отклонения функции 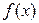от ее интерполяционного многочлена.
Заметим, что в условиях задачи интерполирования не накладываются какие-либо ограничения на функцию 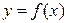. Однако, если предполагать, что аппроксимируемая функция 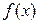на отрезке [ a, b ] непрерывна и имеет все производные 
, 
,…, 
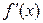до (n +1) – го порядка включительно, то равномерная оценка ее погрешности интерполирования может быть найдена, исходя из вида используемого интерполяционного многочлена [2]. Так, при интерполировании функции 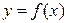по формуле Лагранжа для заданных произвольных значений аргумента x: x 0, x 1, x 2 ,…, xn получена следующая равномерная оценка ее абсолютной погрешности:
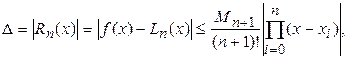(26)
где
; (27)
Для фиксированной точки x = x * оценка погрешности производится по формуле
.
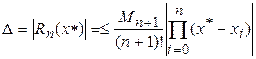Пример 6. Определить точностью, с которой можно вычислить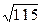 
по интерполяционной формуле Лагранжа для функции 
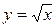, выбрав узлы интерполирования 
, 
, 
.
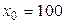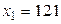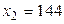Решение. Поскольку заданы три узла интерполирования, найдем производные до третьего порядка включительно функции 
:
, 
, 
.
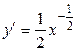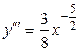По формуле (27) получим
.
По формуле (26) находим:
.
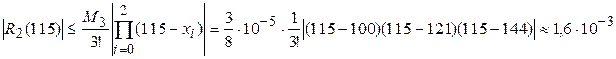При использовании формул Ньютона (20), (25) оценка погрешности найденных значений интерполируемой функции несколько упрощается. Эти формулы получены для равноотстоящих узлов интерполирования x 0, x 1, x 2 ,…, xn, образующих арифметическую прогрессию: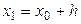 
, 
,…, 
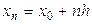, где h – шаг изменения аргумента. Выполнив постановку в формуле (26) переменной t
,
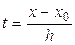получим
. (28)
Эта формула позволяет определить равномерную оценку первой интерполяционной формулы Ньютона.
Аналогично, полагая в формуле (26) 
, получим равномерную оценку второй интерполяционной формулы Ньютона
.
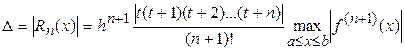Обычно в практике вычислений интерполяционная формула Ньютона обрывается на членах, содержащих разности, которые в пределах точности можно считать постоянными. Предполагая, что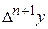 
почти постоянны для функции 
и h мало, и учитывая, что
,
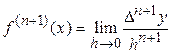приближенно можно принять
.
Тогда остаточный член первой интерполяционной формулы Ньютона приближенно равен
.
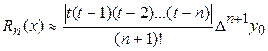Для аналогичных условий остаточный член второй интерполяционной формулы Ньютона приближенно равен
.
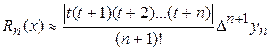Литература.
1. Данилина Н.И. и др. Вычислительная математика: Учеб. пособие для техникумов. – М.: Высш. шк., 1985, с. 256-287, 294-298, 306-308.
2. Демидович Б.П. Основы вычислительной математики: Учеб. пособие для высш. техн. учеб. заведений. М.: ФИЗМАТЛИТ, 1960, с. 497-519, 527-539.
3. Копченова Н.Н., Марон И.А. Вычислительная математика в примерах и задачах. Учеб. пособие. – СПб.: Изд-во «Лань», 2008, с. 100-107, 113-117.
4. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2005, с. 31-36,47-58.
5. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. М.: Изд-во «Наука» 1970, с. 93-128, 133-135.
Контрольные вопросы и упражнения для приобретения