Первая интерполяционная формула Ньютона

Пусть для функции заданы значения для равноотстоящих значений аргумента 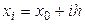(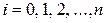), где h - шаг интерполяции. Необходимо подобрать многочлен степени не выше n, принимающий в точках x_i значения

. (15)

Следуя Ньютону, запишем искомый многочлен в виде

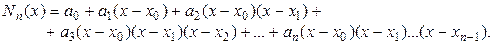(16)

Найдем коэффициенты этого многочлена. Так как в узле 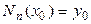, то из (16) получим .

Для узла имеем . Учитывая, что и , находим . Отсюда

.

Для узла многочлен (16) принимает вид

.

Подставив в него полученные значения a ₀, a ₁ и учитывая, что , и , получим

. (17)

Выше было показано (п. 4.1), что значение функции в узле можно найти, зная конечные разности этой функции в узле x ₀ аргумента x, по формуле (14)

,

в которой . Используя эту формулу для узла , получим

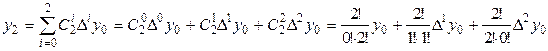
или в конечном виде

. (18)

Из (17)-(18) находим .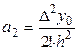

Применяя формулу (14) для узла , получим . Последовательно продолжая этот процесс, заметим, что любой i –й коэффициент многочлена (16) может быть найден по формуле

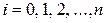, , в которой .

Подставляя найденные выражения коэффициентов в формулу (16), получим интерполяционный многочлен, который называют первой интерполяционной формулой Ньютона

(19)

Сравним полученную формулу Ньютона с формулой Лагранжа (8)

.

В формуле Лагранжа каждое из слагаемых представляет многочлен n -й степени и все эти слагаемые равноправны. Поэтому мы не можем заранее до выполнения вычислений пренебречь какими-либо из них. В формуле Ньютона (19) входят в качестве слагаемых многочлены повышающихся степеней, причем коэффициентами при них являются последовательные разности, деленные на факториал номера слагаемого. Обычно величина последовательных разностей быстро уменьшается. Отсюда возникает возможность не учитывать в формуле Ньютона те слагаемые, коэффициенты которых становятся пренебрежимо малыми. Благодаря этому можно вычислять промежуточные значения функции достаточно точно, пользуясь простыми интерполяционными формулами.

При практическом применении формулы Ньютона ее видоизменяют путем введения новой переменной

.

Тогда формула (19) принимает вид

(20)

Примечание. С точки зрения точности результата интерполирования эту формулу выгодно использовать при вычислении значения функции для значений аргумента x в окрестности начального значения x ₀, где t < 1, т. е. в интервале (x ₀, x ₁). Переходя же к интервалу x ₁ < x < x ₂, нецелесообразно использовать ту же формулу, т. к. t будет больше единицы. В этом случае следует брать за x ₀ следующий узел интерполяции, т. е. x ₁.

Пример 3 [2]. Построить на отрезке [3,5; 3,6] интерполяционный многочлен Ньютона для функции , заданной таблицей

3,50	33,115
3,55	34,813
3,60	36,598
3,65	38,475
3,70	40,447

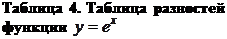Решение. Дополним приведенную таблицу конечными разностями функции , записывая их, как принято, в единицах последнего разряда значений функции без нулей впереди (таблица 4). Поскольку разности третьего порядка практически постоянны, то в формуле (20) принимаем . Тогда при , получим

,

где .

Пример 4 [2]. В таблице 5 приведены значения интеграла вероятностей 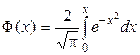и конечные разности функции . По формуле Ньютона найти приближенное значение .

1,0	0,8427		-74
1,1	0,8802		-64
1,2	0,9103		-54
1,3	0,9440		-45
1,4	0,9523		-36
1,5	0,9661		-27
1,6	0,9763		-22
1,7	0,9838
1,8	0,9891

Учитывая вышеприведенное примечание, за x ₀ принимаем ближайшее к заданному его табличное значение, т.е. . Следовательно, . Подставив в формулу (20) это значение t, получим:

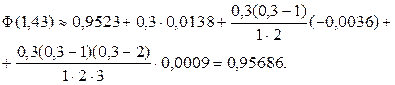
Из приведенных примеров можно заметить, что первая интерполяционная формула Ньютона не позволяет найти искомое значение функции с достаточной точностью в конце таблицы, например в интервале [1,6; 1,8], вследствие отсутствия требуемого числа разностей.

Так, в таблице 5 примера 4 для имеются только первая и вторая разности, а для только первая разность. Вместе с тем, для построения многочлена третьей степени необходимо наличие конечных разностей до третьего порядка включительно.