Конечные разности функций
При рассмотрении задачи интерполирования не накладывались никакие ограничения на значения аргумента x, т. е. они могут быть произвольными, но отличными друг от друга. Здесь и далее будем предполагать, что значения аргумента интерполируемой функции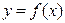 
являются равноотстоящими, т.е. образуют арифметическую прогрессию: 
, 
,…, 
, где h – шаг изменения аргумента (разность арифметической прогрессии). Такая ситуация обычно имеет место при интерполировании функций, заданных в виде таблиц с постоянным шагом.
Пусть, например, функция 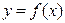задана в точках 
, , 
,…, 
своими значениями: 
, 
, 
,, 
. Составим разности значений функции
;
;
…………………………………………………
.
Выражения, обозначенные через 
, 
,, 
- называются первыми конечными разностями или разностями первого порядка функции 
. По этим выражениям можно составить разности второго порядка
; 
;…, 
.
Аналогично определяются конечные разности третьего и более высокого порядка. Например, конечная разность k - го порядка в точке xm имеет вид:
.
Эти последовательные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной (таблица 1) или диагональной (таблица 2) таблиц разностей.
| 
| 
| 
| 
|
| 
| 
| 
| 
|
| 
| 
| 
| 
|
| 
| 
| 
| 
|
| … | … | … | … | … |
| … | … | … | … | … |
|
|
|
|
|
| |
|
|
| ||||
| |||||
|
|
| 
| |||
| 
| ||||
|
|
| 
| |||
| |||||
| 
| ||||
| … | … | … | … | … |
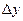
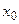
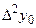
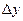
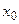
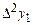
Конечные разности можно вычислить непосредственно через значения функции 
, например,
так как 
и 
, то
.
Аналогично
;
Методом математической индукции нетрудно доказать общую формулу вычисления конечной разности k – го порядка функции 
для любой произвольной точки xm через последовательные значения этой функции
(13)
где 
- число сочетаний из k элементов по i элементов в каждом сочетании 
.
Зная конечные разности функции в узлах сетки аргумента x, можно найти значение этой функции в любом k – м узле. Так из 
находим 
.
Аналогично
.
Так как , то 
. Следовательно
.
Продолжая этот процесс до k – го узла включительно, получим
или в краткой форме
. (14)
Конечные разности обладают следующими свойствами:
1. Если C постоянная величина, то 
;
2. 
;
3. 
;
4. Для степенной функции 
(n - целое) конечная разность равна
.
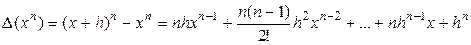Из последнего свойства следует, что конечная разность первого порядка для функции представляет собой многочлен степени n -1. Этот вывод распространяется для конечных разностей многочлена вида
,
т.е. конечная разность первого порядка многочлена n - й степени будет представлять сбой многочлен степени n -1, вторая разность – многочлен степени n -2 и т.д. При этом справедливо утверждение: если
– полином n – й степени, то 
(
) и при k > n разность 
.
| 
| 
| 
| 
|
| 1,0 | 0,00 | -16 | ||
| 1,2 | -0,16 | -8 | ||
| 1,4 | -0,24 | |||
| 1,6 | -0,24 | |||
| 1,8 | -0,16 | |||
| 2,0 | 0,00 | |||
| 2,2 | 0,24 |
Пример 2 [6]. В таблице 3 приведены значения функции 
. Запишем их разности. Обычно разности функций являются небольшими и их принято записывать в единицах последнего разряда значений функции без нулей впереди.
Анализ приведенных разностей показывает, что вторые разности 
постоянны для всех узлов аргумента x, а третьи разности равны нулю. Это полностью согласуется с приведенным выше утверждением.