Погрешность метода
Постановка задачи. Дано дифференциальное уравнение
(5)
и начальное условие: 
. Найти функцию 
, удовлетворяющую как заданному уравнению, так и начальному условию.
Как отмечено выше, при численном решении дифференциального уравнения, не определяя формулу неизвестной функции 
, вычисляют ее последовательные значения yi, соответствующие дискретным значениям xi независимой переменной x. Обычно отрезок [ a, b ], на котором отыскивается решение дифференциального уравнения, разбивается на n равных отрезков. В результате получают последовательность значений (узлов) 
, где 
. Величину 
называют шагом интегрирования дифференциального уравнения
Метод Эйлера основан на разложении искомой функции 
в ряд Тейлора в h -окрестностях узлов 
. Для узла 
это разложение имеет вид
(6)
Так как h мало, то, пренебрегая членами, содержащими h во второй и более высоких степенях в виду их малости, получим
.
Определяя производную 
из исходного дифференциального уравнения (5), подставив в него начальное условие 
, находим приближенное значение искомой функции y при малом смещении h от начальной точки x 0:
.
Теперь, используя полученное значение 
в узле 
, можно вычислить значение 
искомой функции 
в следующей точке 
:
.
Продолжая этот процесс, последовательно находим приближенные значения 
искомой функции в точках 
. Таким образом, вычисление по методу Эйлера решений дифференциального уравнения в узлах 
отрезка [ a, b ] производится по формуле
, (7)
где 
.
Пример. Методом Эйлера проинтегрировать на отрезке [0; 0,4] дифференциальное уравнение 
при начальных условиях 
, приняв 
.
Решение.
1) вычислим решение 
в точке 
. Имеем начальные данные: 
. Используя их, находим
.
По формуле (7), получим
.
2) найдем решение в точке 
. Имеем: 
.
Используя их, получим
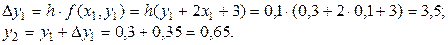
3) выполняя аналогичные действия, найдем:
.
Геометрический смысл метода Эйлера заключается в том, что интегральную кривую 
заменяют на интервале [ x 0, x 1] отрезком касательной к ней, проходящей через точку 
. Угловой коэффициент этой касательной, как видно из рисунка 3, составляет
.
При этом решение дифференциального уравнения в точке 
имеет вид
.
Затем из полученной точки 
проводят новый отрезок касательной, но уже к той интегральной кривой , которая проходит через эту точку, и находят решение для значения независимой переменной 
:
.
Продолжая построение отрезков касательных, получают ломаную линию (ломаную Эйлера), каждое звено которой проведено по касательной к интегральной кривой, проходящей через начальную точку соответствующего звена. Таким образом, ломаная Эйлера проходит через заданную исходную точку и аппроксимирует искомую интегральную кривую .
Заметим, что получение в каждом узле 
интервала 
решения, принадлежащего новой интегральной кривой, обусловливает погрешность метода Эйлера. Величина 
этой погрешности определяется отброшенными членами в разложении искомого решения в ряд Тейлора (6). На каждом шаге построения решения 
погрешность пропорциональна 
, так как именно члены такого порядка отброшены в (6). Однако легко убедиться (рисунок 3), что при последовательном построении решений 
в узлах 
наблюдается суммирование погрешностей, имеющих место на предыдущих шагах интегрирования дифференциального уравнения. Поэтому суммарная погрешность будет пропорциональна 
или, учитывая 
, пропорциональна 
. Следовательно, с увеличением числа узлов в интервале , т. е. с уменьшением шага интегрирования , ломаная Эйлера как угодно близко будет приближаться к искомой интегральной кривой.
На рисунке 4 приведена схема алгоритма интегрирования дифференциального уравнения по методу Эйлера. Здесь блоки 4-7 организуют цикл вычисления таблицы значений искомых решений в узлах интервала 
изменения независимой переменной x. Блок 3 задает начальные условия интегрирования уравнения.
Метод Эйлера наиболее простой метод решения задачи Коши. Однако, в связи с малой точностью, используется сравнительно редко, главным образом, для ориентировочных расчетов. Вместе с тем идея, положенная в основу метода (разложение искомого решения в ряд Тейлора) является исходной для ряда других методов, в том числе метода Рунге-Кутта.