Решения дифференциальных уравнений первого порядка

Лекция 7

2018/2019 уч. г.

 

Раздел 3. Приближенное решение дифференциальных уравнений

Лк –6 ч., ПЗ – 18 ч., СРС – 41 ч.

 

Тема 9. Численные методы решения обыкновенных

Дифференциальных уравнений.

Лк –2 ч., ПЗ – 6 ч., СРС – 12 ч.

1. Основные понятия о дифференциальном уравнении. Задача Коши. Методы решения дифференциальных уравнений первого порядка.

2. Метод Эйлера, его геометрический смысл. Погрешность метода.

3. Метод Рунге-Кутта. Оценка погрешности метода.

4. Применение методов Эйлера и Рунге-Кутта для решения систем дифференциальных уравнений и дифференциальных уравнений высших порядков.

 

Литература.

1. Данилина Н.И. и др. Вычислительная математика: Учеб. пособие для техникумов. – М.: Высш. шк., 1985.

2. Демидович Б.П. Основы вычислительной математики: Учеб. пособие для высш. техн. учеб. заведений. М.: ФИЗМАТЛИТ, 1960.

3. Копченова Н.Н., Марон И.А. Вычислительная математика в примерах и задачах. Учеб. пособие. – СПб.: Изд-во «Лань», 2008.

4. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2005.

 

 

Основные понятия о дифференциальном уравнении. Методы

решения дифференциальных уравнений первого порядка

 

Уравнение, в которое неизвестная функция входит под знаком производной или дифференциала называется интегральным уравнением, например, уравнения

, .

являются дифференциальными уравнениями, так как в них неизвестные функции и находятся под знаком производной и дифференциала.

Различают обыкновенные дифференциальные уравнения, в которых неизвестная функция зависит только от одной независимой переменной, и уравнения с частными производными, в которых неизвестная функция является функцией от двух или большего числа независимых переменных.

 

Например, дифференциальное уравнение

есть уравнение в частных производных.

В данной теме рассматриваются только обыкновенные дифференциальные уравнения, которые в дальнейшем для удобства изложения именуются просто дифференциальными уравнениями.

Наивысший порядок n входящей в уравнение производной (или дифференциала) называется порядком дифференциального уравнения. Так уравнения

,

являются дифференциальными уравнениями второго и третьего порядка соответственно.

В самом общем случае дифференциальное уравнение n - го порядка содержит независимую переменную, неизвестную функцию и ее производные или дифференциалы до n - го порядка включительно и имеет вид

(1)

Если левая часть уравнения (1) представляет собой многочлен k - й степени по отношению к производной от неизвестной функции, то степень этого многочлена называется степенью дифференциального уравнения. Например, уравнение

является уравнением второго порядка четвертой степени.

Уравнение, линейное относительно неизвестной функции и ее производных, называется линейным дифференциальным уравнением. в частности, уравнение 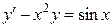- линейное уравнение первого порядка.

Решением (или интегралом) дифференциального уравнения называется всякая дифференцируемая функция , которая при ее подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой этого уравнения. Любое дифференциальное уравнение имеет бесконечное множество решений. Например, решением дифференциального уравнения

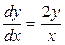
является функция 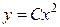, представляющая семейство кривых (парабол) на координатной плоскости x 0 y (рисунок 1). Это бесконечное множество функций 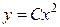, зависящее от произвольной постоянной и удовлетворявшее дифференциальному уравнению, называется общим решением (или общим интегралом). Общее решение дифференциального уравнения n - го порядка содержит n произвольных постоянных C ₁, C ₂,…, C_n и имеет вид .

Частное решение дифференциального уравнения получают из общего, задавая произвольным постоянным определенные числовые значения. Так, если в приведенном выше примере, задать произвольной постоянной C значение C = 2, получим частное решение .

Обычно при отыскании частного решения произвольные постоянные, входящие в общее решение, определяются из так называемых начальных условий. При этом задача поиска частного решения формулируется следующим образам:

найти решение уравнения

, (2)

удовлетворяющее дополнительным условиям, состоящим в том, что решение должно принимать вместе со своими производными до (n -1) - го порядка заданные числовые значения при заданном числовом значении 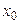независимой переменной , т.е. при :

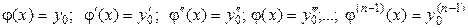. (3)

Условия (3) называются начальными условиями; числа - начальными данными задачи, а задача поиска решения дифференциального уравнения (2), удовлетворяющего начальным условиям (3) – задачей с начальными условиями или задачей Коши.

В случае уравнения первого порядка (n =1) имеем задачу для уравнения с начальным условием . Геометрически такая задача состоит в том, чтобы из всего множества интегральных кривых, представляющих общее решение, выделить ту кривую, которая проходит через точку .

Например, найдем частное решение уравнения с начальным условием . Общее решение, как показано выше, имеет вид 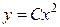. Подставляя в него начальные данные, получим , откуда . Следовательно, частное решение, удовлетворяющее заданному начальному условию, есть 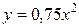. Геометрически это решение представляет собой параболу, проходящую через точку M ₀(2,3) (рисунок 1).

Кроме задачи Коши, в инженерной практике встречается другой тип задач – краевые задачи. В этих задачах дополнительные условия задаются для нескольких значений независимой переменной. Дополнительные условия при этом называются граничными или краевыми. Обычно граничные условия задаются в двух точках , являющихся границами области решения дифференциального уравнения.

 

 

Например, поиск решения дифференциального уравнения вида

с граничными условиями

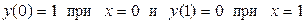
представляет собой краевую задачу.

Все методы решения дифференциальных уравнений первого порядка можно условно разбить на точные и приближенные. Точные методы заключаются, главным образом, в приведении исходных дифференциальных уравнений к уравнениям с разделенными переменными с последующим их интегрированием. При этом получают решение в виде аналитической зависимости . Однако число типов уравнений, позволяющих получить точное решение, сравнительно невелико. Кроме того, нередко точное решение дифференциального уравнения может иметь вид, неудобный для дальнейшего практического использования. Например, уравнение

имеет решение в виде: . Такое решение при вычислении значения искомой функции y для заданного значения аргумента x потребует, в свою очередь, поиска решения трансцендентного уравнения.

Большое применение в инженерной практике имеют методы приближенного решения дифференциальных уравнений. Эти методы в зависимости от формы представления решения подразделяются на три группы: графические, аналитические и численные.

Графические методы позволяют получить решение в виде графика искомой функции . Они основаны на геометрическом смысле дифференциального уравнения. В частности, дифференциальное уравнение первого порядка вида

, (4)

где задана в некоторой области D на плоскости x 0 y (рисунок 2) определяет в каждой точке (x, y) области D угловой коэффициент (направление) касательной к интегральной кривой, проходящей через эту точку. Таким образом, геометрически уравнение (4) задает в области D поле направлений и, следовательно, задача интегрирования этого уравнения заключается в нахождении кривых, направление касательных к которым совпадает с направлением поля в соответствующих точках.

Такое геометрическое представление дифференциального уравнения (4) позволяет проинтегрировать его графически, т.е. приближенно отобразить на чертеже общую картину хода интегральных кривых. Для этого область D покрывают густой сеткой точек и в каждой выбранной точке (x_i, y_i) наносят небольшую стрелку, наклоненную под углом α_i к оси 0 x, где . Затем по направлению построенных стрелочек проводят линии, которые приближенно представляют собой интегральные кривые данного дифференциального уравнения.

Наиболее простыми из графических методов являются метод ломаных Эйлера и метод изоклин.

Аналитические методы обеспечивают получение приближенного решения дифференциального уравнения в виде аналитического выражения искомой функции. Эти методы используют различные подходы поиска приближенного решения, в частности, упрощения исходного дифференциального уравнения путем обоснованного отбрасывания некоторых его членов, представления решения в виде степенного ряда с неопределенными коэффициентами или в виде ряда Тейлора и другие.

В отличие от аналитических методов, численные методы направлены не на определение формулы искомого решения дифференциального уравнения, а на последовательное вычисление его приближенных значений для заданных значений аргумента x. Решение при этом получают в форме таблицы значений.

Поскольку при решении различных технических вопросов обычно требуется не формула, дающая искомое решение, а его числовые значения, то численные методы наиболее часто используются при исследовании научно-технических задач, описываемых дифференциальными уравнениями. Кроме того, эти методы применимы для различных типов дифференциальных уравнений. Однако численные методы не дают общего решения дифференциального уравнения, они позволяют определить только частное решение. Это основной недостаток численных методов.

Для решения обыкновенных дифференциальных уравнений применяют­ся две группы численных методов:

- одношаговые методы, в которых при нахождении для последующего значения 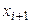независимой переменной x значения искомого решения дифференциального уравнения требуется информация только о значениях и , полученных на предыдущем шаге. К одношаговым методам относятся методы Эйлера, Рунге-Кутта и др.;

- многошаговые методы (методы Адамса, Милна и др.), в которых для отыскания следующей точки (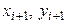) интегральной кривой требуется информация о нескольких предыдущих точках.