Методы Эйлера и Рунге - Кутта могут быть применены для решения системы дифференциальных уравнений первого порядка. Пусть задана система двух уравнений вида
(14)
с начальными условиями:
.
Используя зависимости (10), (12), (13), запишем последовательность формул Рунге-Кутта для вычисления решений 
и 
в произвольной точке интегрирования уравнений (14):
; 
; 
. (15)
При необходимости численного интегрирования дифференциального уравнения n - го порядка его предварительно способом подстановки приводят к системе из n дифференциальных уравнений первого порядка. Например, рассмотрим задачу Коши для уравнения второго порядка
(16)
с начальными условиями
. (17)
Обозначим первую производную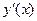 
через вторую неизвестную функцию 
. Подставляя принятое обозначение в (16) и (17), приходим к задаче Коши для системы из двух дифференциальных уравнений первого порядка:
(18)
с начальными условиями
(19)
где 
.
Легко заметить, что уравнения (18) полностью аналогичны уравнениям (14). Их отличает только то, что в качестве выражения 
в правой части первого уравнения системы (14) выступает неизвестная функция z. Однако, это не вызывает каких-либо затруднений при применении формул (15) вычисления значений неизвестных функций y (x) и z (x) системы (18).
Если система уравнений (18) решается методом Эйлера, то значения неизвестных функций y (x) и z (x) в точках xi интервала интегрирования вычисляются по формулам:
, 
,
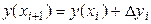в которых
.
Замечания.
1. Особенностью одношаговых методов является то, что для получения решения дифференциального уравнения в каждом новом узле xi +1 достаточно иметь значение y (xi) неизвестной функции лишь в одном предыдущем узле. Это свойство называют "самостартованием". Свойство "самостартования" позволяет изменять величину шага интегрирования h в процессе вычисления решения в любом узле и тем самым допускает построение алгоритмов численного интегрирования дифференциальных уравнений с автоматическим выбором шага.
2. В основе одношаговых методов лежит разложение искомого решения в ряд Тейлора с сохранением членов, содержащих h в степени до k включительно. Целое число k называется порядком метода. В частности, рассмотренные методы Эйлера и Рунге-Кутта являются методами первого и четвертого порядков соответственно.
Серьезным недостатком одношаговых методов является отсутствие простых способов оценки погрешности найденных решений. Как показано выше, эта погрешность пропорциональна hk (k - порядок метода). Грубую оценку погрешности решения можно найти с помощью двойного просчета по формуле
где 
- значение точного решения дифференциального уравнения в точке 
; 
, 
- приближенные значения при шаге интегрирования h /2 и h соответственно.
3. Поскольку погрешность решения пропорциональна шагу интегрирования hk то для получения решения с точностью ε рекомендуется шаг выбирать, исходя из условия hk < ε.
При этом шаг h можно изменять при переходе от одной точки к другой. Для оценки правильности выбора шага при интегрировании методом Рунге - Кутта используют равенство
Если q больше нескольких сотых, то шаг интегрирования необходимо уменьшить.
Контрольные вопросы и упражнения для приобретения