Для построения диаграммы удельных равнодействующих сил, необходимой для выполнения тяговых расчетов, выполняют вычисления, результаты которых сводят в таблицу, приведенную на рисунке 5. Вычисления обычно выполняют для трех режимов ведения поезда: режима тяги, режима холостого хода (выбега) и режима торможения (служебного и экстренного).
Порядок заполнения таблицы следующий. Первые два столбца таблицы заполняют данными тяговой характеристики локомотива. Шаг изменения скорости не должен превышать 10 км/ч. Кроме того, в таблицу необходимо внести значения, соответствующие характерным точкам тяговой характеристики. Такими значениями являются: скорость перехода от ограничения по сцеплению (по току) на автоматическую характеристику, расчетная скорость и скорости изменения режима работы тяговых электродвигателей. Так в таблице на рисунке 5 приведены данные, принятые по тяговой характеристике тепловоза 2ТЭ10М. Характерными значениями скорости для 15-й позиции контроллера машиниста являются: 19 км/ч – скорость выхода на автоматическую характеристику; 23,4 км/ч – расчетная скорость; 38 км/ч – переход от ПП к ОП1; 62,5 км/ч – переход от ОП1 к ОП2; 43 км/ч – переход от ОП2 к ОП1 и 27,5 км – переход от ОП1 к ПП. Для тех значений скорости, при которых возможна работа на двух режимах работы тяговых электродвигателей, принимают среднее значение силы тяги. Например, при 15-й позиции контроллера машиниста на скорости движения поезда v = 50 км/ч возможна работа тяговых электродвигателей на ОП1 или ОП2. При ОП1 сила тяги F к = 125000 Н, а при ОП2 F к = 126000 Н.
 В таблицу следует записать F к = 125500 Н. В столбцах С и D помещают значения основного удельного и полного сопротивления движению локомотива при движении в режиме тяги. Удельное сопротивление:
В таблицу следует записать F к = 125500 Н. В столбцах С и D помещают значения основного удельного и полного сопротивления движению локомотива при движении в режиме тяги. Удельное сопротивление:
| – для звеньевого пути | ||
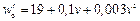 ; ;
| ||
| – для бесстыкового пути | ||
 . .
|
Основное сопротивление движению локомотива 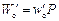 .
.
Для вычисления основного удельного сопротивления движению состава предварительно рассчитывают основное удельное сопротивление движению каждой из входящих в состав групп вагонов. Вычисления выполняют в соответствии с приведенными ниже выражениями.
Основное сопротивление движению грузовых вагонов на звеньевом пути. Для груженых вагонов при массе, приходящейся на ось колесной пары, q o > 6 т/ось:
| а) четырехосные вагоны на роликовых подшипниках и вагоны рефрижераторных поездов: | |||
 ; ;
| |||
| б) шестиосные вагоны на роликовых подшипниках и четырехосные вагоны на подшипниках скольжения: | |||
 . .
| |||
| Для порожних вагонов (q o ≤ 6 т/ось): | |||
| а) четырехосные вагоны на подшипниках скольжения: | |||
 ; ;
| |||
| б) четырехосные и шестиосные вагоны на роликовых подшипниках: | |||
 . .
| |||
| Восьмиосные вагоны на роликовых подшипниках при любой осевой нагрузке: | |||
 . .
| |||
Основное сопротивление движению грузовых вагонов на бесстыковом пути. Для груженых вагонов при массе, приходящейся на ось колесной пары, q o > 6 т/ось:
| а) четырехосные вагоны на роликовых подшипниках и вагоны рефрижераторных поездов: | ||
 ; ;
| ||
| б) шестиосные вагоны на роликовых подшипниках и четырехосные вагоны на подшипниках скольжения: | ||
 . .
| ||
| Для порожних вагонов (q o ≤ 6 т/ось): | ||
| а) четырехосные вагоны на подшипниках скольжения | ||
 ; ;
| ||
| б) четырехосные и шестиосные вагоны на роликовых подшипниках: | ||
 . .
| ||
| Восьмиосные вагоны на роликовых подшипниках при любой осевой нагрузке: | ||
 . .
|
Основное сопротивление движению пассажирских вагонов на звеньевом пути для скоростей движения до 160 км/ч:
| – на звеньевом пути | ||
 ; ;
| ||
| – на бесстыковом пути | ||
 . .
|
Если состав включает вагоны разных типов, то его основное удельное сопротивление движению определяют как средневзвешенное:

| (24) |
где a4 , a6,a8 – соответственно доля четырех, шести или восьмиосных вагонов в общей массе состава.
Вагоны, из которых сформирован состав поезда, можно разделить на группы не только по количеству осей в вагоне, но и по другим признакам, например, по осевой нагрузке. Тогда число слагаемых в формуле (24) вырастет, но всегда при этом Σa i = 1 (i – номер группы однотипных вагонов).
Массу, приходящуюся на ось, для каждого типа вагонов принимают как среднюю. Например, для четырехосных вагонов
 , ,
|
где Q 4 – суммарная масса всех четырехосных вагонов;
4 n 4 – общее число осей всех четырехосных вагонов (n 4), входящих в состав.
Основное сопротивление движению состава  .
.
Столбцы G–I заполняют, выполняя вычисления в соответствии с выражениями:
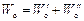 , ,
| ||
 , ,
| ||
 . .
|
Таким образом, в столбце I таблицы записывают значения равнодействующей сил, приходящейся на единицу массы поезда при движении в режиме тяги на максимальной позиции контроллера машиниста.
Затем выполняют расчеты и заполняют столбцы J – M для режима холостого хода (выбега).
В столбце J помещают значения основного удельного сопротивления движению локомотива на холостом ходу, которое вычисляют в соответствии с выражениями:
| а) на звеньевом пути | ||
 ; ;
| ||
| б) на бесстыковом пути | ||
 . .
|
В столбце K записывают значения основного сопротивления движению локомотива на холостом ходу 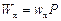 , в столбце L –значение основного сопротивления движению поезда на холостом ходу
, в столбце L –значение основного сопротивления движению поезда на холостом ходу 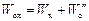 , а в столбце M – значение основного удельного сопротивления движению поезда на холостом ходу
, а в столбце M – значение основного удельного сопротивления движению поезда на холостом ходу  .
.
Прежде чем перейти к расчету и заполнению столбцов N–Q, соответствующих режиму торможения, определяют значение расчетного тормозного коэффициента
 . .
| (25) |
Суммарное расчетное нажатие тормозных колодок вычисляют по числу вагонов каждого вида (n 4, n 6, n 8), входящих в состав поезда, числу осей локомотива заданной серии (n л) и расчетному нажатию на одну тормозную ось для каждого вида вагонов и локомотива:
 . .
| (26) |
Если не все оси в составе тормозные, то это следует учитывать при вычислении суммарного нажатия тормозных колодок. С этой целью суммарное тормозное нажатие для состава  умножают на коэффициент, равный доле тормозных осей в составе. Если доля тормозных осей задана для каждого типа вагонов, то соответствующие коэффициенты умножают на каждое из слагаемых в выражении (26).
умножают на коэффициент, равный доле тормозных осей в составе. Если доля тормозных осей задана для каждого типа вагонов, то соответствующие коэффициенты умножают на каждое из слагаемых в выражении (26).
При расчетах тормозной силы для грузовых поездов, движущихся на участках со спусками до 20 ‰, Правилами тяговых расчетов рекомендуется не принимать в расчет пневматические тормоза локомотива и его массу. Иначе говоря, в формуле (25) можно исключить P, а в формуле (26) исключают слагаемое n л K рл .
Значения расчетного нажатия на одну тормозную ось для отдельных групп вагонов принимают по таблицам 5 и 7, а для локомотивов – по таблице 6.
При чугунных тормозных колодках тормоза грузовых вагонов включают на порожний режим, если полезная загрузка на одну ось не превышает 3 т, на средний - если полезная загрузка на одну ось не превышает 6 т, на груженый при полезной загрузке более 6 т.
Тормоза рефрижераторных вагонов, оборудованных чугунными колодками, включают на средний режим при полезной загрузке до 3 т/ось, а на груженый режим – при большей полезной загрузке.
Таблица 5 – Расчетные силы нажатия тормозных колодок вагонов в пересчете на чугунные
| Тип вагона | Расчетное нажатие тормозных колодок, кН/ось |
| Цельнометаллические пассажирские вагоны с массой тары: | |
| 53 т и более | |
| 48 т и более, но менее 53 т | |
| 42 т и более, но менее 48 т | |
| Цельнометаллические пассажирские вагоны ВЛ-РИЦ с тормозом КЕ и чугунными тормозными колодками: | |
| на пассажирском режиме | |
| на скоростном режиме | |
| Цельнометаллические пассажирские вагоны габарита РИЦ на тележках ТВЗ-ЦНИИ «М» с тормозом КЕ и композиционными тормозными колодками (в пересчете на чугунные колодки*): | |
| на пассажирском режиме | |
| на скоростном режиме | |
| Пассажирские вагоны длиной 20,2 м и менее | |
| Остальные вагоны пассажирского парка |
Окончание таблицы 5
| Тип вагона | Расчетное нажатие тормозных колодок, кН/ось |
| Грузовые вагоны, оборудованные чугунными колодками, на режиме: | |
| груженом | |
| среднем | |
| порожнем | |
| Грузовые вагоны, оборудованные композиционными колодками (в пересчете на чугунные колодки*), на режиме: | |
| груженом | |
| среднем | |
| порожнем | |
| Четырехосные изотермические и багажные цельнометаллические с односторонним торможением | |
| Вагоны рефрижераторного подвижного состава с чугунными тормозными колодками на режиме: | |
| груженом | |
| среднем | |
| порожнем | |
| Вагоны рефрижераторного подвижного состава с композиционными тормозными колодками (в пересчете на чугунные колодки) на режиме: | |
| среднем | |
| порожнем |
Таблица 6 – Расчетные силы нажатия чугунных тормозных колодок локомотивов, дизель- и электропоездов
| Серия локомотивов | Расчетное нажатие тормозных колодок, кН/ось | |
| груженый режим | порожний режим | |
| Тепловозы | ||
| ТЭ1, ТЭП60, 2ТЭП60, 2ТЭ10В(М,У), 3ТЭ10М, 4ТЭ10С, 2ТЭ116, ТЭП70, ТЭП75, ТЭП80, 2ТЭ121, 2М62, 2М62У, 3М62У | ||
| ТЭП10, ТЭ7 | – | |
| ТЭМ7, ТЭМ7А | ||
| ТЭ2, ТГ102 | ||
| ЧМЭ3, ЧМЭ3т, ЧМЭ3э,ТЭМ2УМ, ТЭМ2У, ТЭМ16, ТЭМ17, ТЭМ18, ТЭМ2А | ||
| ТГ21, ТГ22 | ||
| ТГМ3А | ||
| Остальные серии тепловозов |
Окончание таблицы 6
| Серия локомотивов | Расчетное нажатие тормозных колодок, кН/ось | |
| груженый режим | порожний режим | |
| Электровозы | ||
| ЧС1, ЧС3 | – | |
| ЧС2, ЧС2т, ЧС4, ЧС4 т, ЧС6, ЧС7, ЧС8, ЧС200: | ||
| скоростной режим | – | |
| то же при скоростях менее 60 км/ч и пассажирском режиме | – | |
| ВЛ80, ВЛ80к, ВЛ80т, ВЛ80с, ВЛ80п, ВЛ80р, ВЛ82, ВЛ82м, ВЛ85, ВЛ10, ВЛ10у, ВЛ11, ВЛ11м,ВЛ15, ВЛ-65, Э13 | ||
| ВЛ23, ВЛ60 всех индексов | ||
| ЭП1 на скоростном режиме | – | |
| ЭП1 на скоростном режиме при скоростях менее 55 км/ч и пассажирском режиме | – | |
| Остальные серии электровозов | ||
| Дизель-поезда | ||
| Серии Д, моторный вагон | – | |
| Серии Д, прицепной вагон | – | |
| Серии ДР1, Д1, ДР1П, ДР1А, моторный вагон | – | |
| Серии ДР1, Д1, ДР1П, ДР1А, прицепной вагон | – | |
| Серии ДЛ2, тяговая секция | – | |
| Серии ДЛ2, прицепной вагон | – | |
| Электропоезда | ||
| Моторные вагоны (кроме ЭД9Т) | – | |
| Моторные вагоны ЭД9Т | – | |
| Прицепные и головные вагоны | – | |
| Моторный и головой вагоны ЭР200 | – |
Таблица 7 – Расчетные силы нажатия композиционных тормозных колодок вагонов
| Тип вагона | Расчетное нажатие тормозных колодок, кН/ось |
| Пассажирские вагоны с массой тары: | |
| 53 т и более | |
| 48 т и более, но менее 53 т | |
| 42 т и более, но менее 48 т | |
| Грузовые вагоны на режиме: | |
| груженом | 42,5 |
| среднем | |
| порожнем | 17,5 |
| Рефрижераторные вагоны-холодильники: с передаточным числом рычажной передачи 5,3 на режиме: | |
| груженом |
Окончание таблицы 7
| Тип вагона | Расчетное нажатие тормозных колодок, кН/ось |
| среднем | |
| порожнем | |
| с передаточным числом рычажной передачи 10 на режиме: | |
| среднем | 47,5 |
| порожнем |
В столбце N записывают значения расчетного коэффициента трения колодки 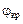 , которые рассчитывают для значений скорости, приведенных в столбце A, по следующим формулам:
, которые рассчитывают для значений скорости, приведенных в столбце A, по следующим формулам:
для стандартных чугунных колодок
 ; ;
| (27) |
чугунных колодок с повышенным содержанием фосфора
 ; ;
| (28) |
чугунных колодок из высокофосфористого чугуна (3 %)
 ; ;
| (29) |
композиционных колодок из материала 8-1-66
 . .
| (30) |
композиционных колодок из материала 328-303
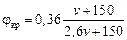 . .
| (31) |
В столбце O записывают значения удельной тормозной силы, вычисленные по формуле
 . .
| (32) |
В столбце P записывают значение равнодействующей сил, приложенных к поезду на режиме служебного торможения, для грузовых поездов
 , ,
| (33а) |
и для пассажирских поездов
 , ,
| (33б) |
а в столбце Q – для экстренного торможения
 . .
| (34) |
Так же, как и при спрямлении профиля пути, эти расчеты удобно выполнять в среде Microsoft Excel. Пример организации таких вычислений и приведен на рисунке 5. Для расчета необходимо заполнить первые два столбца таблицы данными из тяговой характеристики локомотива и ввести исходные данные, помещенные на рисунке 5 под таблицей. Таблица заполняется результатами расчета, появляющимися по мере ввода исходных данных. Если предварительно подготовить базу данных о локомотивах, то и процесс ввода тяговой характеристики локомотива может быть автоматизирован.
 По результатам вычислений, приведенным на рисунке 5, строят диаграмму удельных равнодействующих сил, приложенных к поезду (рисунок 6). Эта диаграмма верна только для исходных данных, принятых при ее расчете и построении.
По результатам вычислений, приведенным на рисунке 5, строят диаграмму удельных равнодействующих сил, приложенных к поезду (рисунок 6). Эта диаграмма верна только для исходных данных, принятых при ее расчете и построении.
При изменении характеристик состава или при построении диаграммы для движения в режиме тяги на промежуточных позициях контроллера машиниста необходимо выполнить расчеты для новых исходных данных. В то же время для использования диаграммы при движении на элементах профиля пути с уклонами, отличными от нуля, достаточно перенести начало координат влево для подъемов или вправо для спусков на число единиц, равное уклону в промилле, умноженному на десять. Диаграмма удельных равнодействующих сил позволяет анализировать характер движения поезда, для которого она построена. Зная, что скорость движения поезда всегда стремится к равновесной, достаточно по уклону профиля пути и режиму движения найти значение равновесной скорости и сравнить его с текущим значением скорости движения.
Решение тормозных задач
Для обеспечения безопасности движения поездов важнейшее значение имеет возможность ограничения скорости движения или остановки поезда, выполняемой в штатной или экстраординарной ситуации. А это значит, что при необходимости остановки или ограничения скорости движения должна быть обеспечена эффективность действия тормозов поезда.
Практика эксплуатации подвижного состава поставила задачи, связанные с торможением поездов. С одной стороны, это задача определения тормозных средств, которые могут обеспечить снижение скорости движения или полную остановку поезда на требуемом расстоянии. А с другой стороны, это задача определения расстояния, на котором заданный поезд с известными тормозными средствами может остановиться или снизить скорость движения до заданного значения. Названные задачи называют тормозными задачами. Для решения этих задач можно применить различные методы решения уравнения движения поезда.
Условимся в соответствии с [1] под термином «тормозной путь » понимать расстояние, которое проходит поезд от момента поворота ручки крана машиниста или стоп-крана в тормозное положение до полной остановки поезда. После поворота ручки крана машиниста в тормозное положение проходит некоторое время, прежде чем тормозные колодки соприкоснутся с колесами (тормозными дисками). В силу инерционности тормозной системы, включающей тормозную магистраль, воздухораспределители и рычажную передачу, нарастание тормозной силы до установившегося значения в разных вагонах происходит не одновременно. В расчетах обычно этой инерционностью пренебрегают и считают, что тормозная сила мгновенно вырастает до своего установившегося значения через некоторый отрезок времени t п после поворота крана машиниста в тормозное положение. Этот временной отрезок называют временем подготовки тормозов к действию. Расстояние s п, которое поезд проходит за время подготовки тормозов к действию, называют подготовительным тормозным путем. Расстояние s д, которое поезд проходит с прижатыми тормозными колодками, называют действительным тормозным путем. Таким образом, тормозной путь s т складывается из подготовительного и действительного тормозных путей:
 . (35)
. (35)
Допустив, что поезд проходит путь подготовки тормозов к действию с постоянной скоростью, найдем его значение, м,
 , (36)
, (36)
где v o – скорость поезда в момент начала торможения, км/ч;
t п – время подготовки тормозов к действию, с.
Экспериментально установлено, что время подготовки тормозов к действию изменяется в зависимости от длины состава. Для расчетов обычно принимают значения t п, приведенные в таблице 8.
Таблица 8 – Время подготовки тормозов
| Длина состава и вид тормозов | t п, с |
| Грузовые составы длиной 200 осей и менее при автоматических тормозах или одиночно следующие грузовые локомотивы | |
| Грузовые составы длиной от 200 до 300 осей при автоматических тормозах | |
| Грузовые составы длиной более 300 осей при автоматических тормозах | |
| Пассажирские поезда при электропневматических тормозах |
Учитывая, что в действительности скорость движения поезда за время подготовки тормозов не остается неизменной, вводится поправка, определяемая величиной и знаком уклона, а также величиной тормозной силы. С учетом поправки время подготовки тормозов к действию определяют по формулам:
– для грузовых составов длиной 200 осей и менее при автоматических тормозах и для одиночно следующих грузовых локомотивов
 ; (37)
; (37)
– для грузовых составов длиной более 200 осей (до 300 осей) при автоматических тормозах
 ; (38)
; (38)
– для грузовых составов длиной более 300 осей при автоматических тормозах
 ; (39)
; (39)
– для пассажирских поездов при пневматических тормозах и для одиночно следующих пассажирских локомотивов
 ; (40)
; (40)
– для пассажирских поездов при электропневматических тормозах
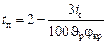 , (41)
, (41)
где i c – приведенный уклон, ‰;
 – расчетный тормозной коэффициент поезда, принятый для случая экстренного торможения;
– расчетный тормозной коэффициент поезда, принятый для случая экстренного торможения;
 – расчетный коэффициент трения тормозной колодки.
– расчетный коэффициент трения тормозной колодки.
При ручных тормозах принимают t п = 60 с.
При срабатывании автостопа время подготовки автоматических тормозов, рассчитанное по одной из приведенных выше формул, увеличивают на 14 с.
Процесс торможения поезда определяется длиной тормозного пути s т, начальной v о и конечной v к скоростью торможения, уклоном пути i и тормозными средствами поезда, определяемыми расчетным тормозным коэффициентом  . К нахождению одной из этих величин по известным остальным и сводится решение тормозных задач, которые условно можно разделить на две группы.
. К нахождению одной из этих величин по известным остальным и сводится решение тормозных задач, которые условно можно разделить на две группы.
К первой группе относят задачи, для которых известны тормозные средства поезда, а определить необходимо одну из трех величин: тормозной путь, начальную или конечную скорость торможения.
Ко второй группе относят задачи, для которых тормозные средства поезда следует определить по известным значениям тормозного пути, начальной и конечной скорости торможения.
Рассмотрим задачу определения тормозного пути, относящуюся к первой группе тормозных задач. Для нахождения длины тормозного пути необходимо решить уравнение движения поезда для режима торможения. Сначала необходимо найти путь подготовки тормозов, используя формулы (37)–(41). Затем, интегрируя уравнение движения поезда, находят действительный тормозной путь.
При аналитическом интегрировании уравнения движения поезда весь диапазон изменения скорости от начальной до конечной разбивают на интервалы. Для каждого из интервалов изменения скорости находят путь, который проходит поезд. Суммарное значение действительного тормозного пути, м,
 , (42)
, (42)
где  – значения начальной и конечной скорости движения поезда на рассматриваемом i- м интервале, км/ч;
– значения начальной и конечной скорости движения поезда на рассматриваемом i- м интервале, км/ч;
 – среднее на i- м интервале изменения скорости значение удельной равнодействующей сил, приложенных к поезду, Н/т,
– среднее на i- м интервале изменения скорости значение удельной равнодействующей сил, приложенных к поезду, Н/т,
 . (43)
. (43)
Графическое определение длины тормозного пути. В прямоугольных координатах (рисунок 7), выбрав масштабы из таблицы 13, строим диаграмму замедляющих сил для режима торможения и рядом откладываем по оси абсцисс расстояние, равное пути подготовки тормозов s п , вычисленное в соответствии с выражением (36).
На уровне скорости начала торможения v н проводим горизонтальную линию, соответствующую постоянной скорости в пределах пути подготовки тормозов. Затем, разбив весь диапазон изменения скорости от v н до нуля на интервалы не более 10 км/ч, строим способом Липеца кривую скорости от координаты окончания пути подготовки тормозов и до точки, в которой значение скорости становится равным нулю. Расстояние s т и является искомой длиной тормозного пути.
Рассмотрим на примерах решение различных задач, относящихся к первой группе тормозных задач.
Пример 6. Определить длину тормозного пути грузового поезда с составом массой Q = 4980 т, состоящего из четырехосных вагонов на роликовых подшипниках, движущегося по звеньевому пути на спуске i = –5 ‰, начинающего экстренное торможение при скорости 70 км/ч. Средняя осевая нагрузка вагонов q o = 15 т/ось. Тормозные колодки чугунные. Все оси тормозные. Массой и тормозными средствами локомотива пренебречь.
Решение.Полный тормозной путь складывается из пути подготовки тормозов и действительного тормозного пути.
Чтобы вычислить путь подготовки тормозов по формуле (36), необходимо найти время подготовки тормозов t п в соответствии с одним из выражений (37)–(41). Чтобы выбрать расчетное выражение, найдем число осей в составе:

 оси.
оси.
Значение расчетного тормозного коэффициента при расчетном нажатии чугунных колодок на груженом режиме 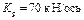
 .
.
Значение расчетного коэффициента трения чугунных тормозных колодок о колесо при скорости v = 70 км/ч
 .
.
Поскольку  время подготовки тормозов по формуле (39)
время подготовки тормозов по формуле (39)
 c,
c,
а путь подготовки тормозов
 м.
м.
Действительный тормозной путь вычислим по формуле (42) последовательно для каждого из интервалов изменения скорости, равных 10 км/ч.
Определим среднее значение удельной замедляющей силы при снижении скорости движения от 70 до 60 км/ч. Для этого найдем основное удельное сопротивление и удельную тормозную силу для средней на рассматриваемом интервале скорости движения v = 65 км/ч:
 Н/т;
Н/т;
 ;
;
 Н/т.
Н/т.
Откуда 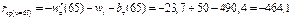 Н/т.
Н/т.
При снижении скорости движения от 70 км/ч до 60 км/ч поезд пройдет расстояние
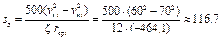 м.
м.
Сведем расчеты в таблицу 9.
Таким образом, действительный путь торможения  м, а полный тормозной путь
м, а полный тормозной путь  м.
м.
Таблица 9 – Расчет длины тормозного пути
| v 1, км/ч | v 2, км/ч | v ср, км/ч | φкр | b т, Н/т |  , Н/т , Н/т
| r ср, Н/т | Si , м | Σ Si , м |
| 0,105 | 490,4 | 23,7 | -464,1 | 116,7 | 116,7 | |||
| 0,112 | 523,0 | 21,0 | -490,4 | 92,8 | 209,5 | |||
| 0,120 | 560,4 | 18,7 | -529,1 | 70,9 | 280,4 | |||
| 0,133 | 621,1 | 16,7 | -587,8 | 49,6 | 330,0 | |||
| 0,150 | 700,5 | 15,0 | -665,5 | 31,3 | 361,3 | |||
| 0,177 | 826,6 | 13,7 | -790,3 | 15,8 | 377,1 | |||
| 0,227 | 1060,1 | 12,7 | -1022,8 | 4,1 | 381,2 |
Пример 7. Определить наибольшую скорость, с которой поезд из примера 6 должен двигаться, чтобы при экстренном торможении остановиться на расстоянии не более 600 метров.
Решение. Допустим, что путь подготовки тормозов зависит только от скорости движения и изменяется линейно. Тогда найдем две точки, которые определяют эту прямую. Первая точка соответствует скорости v = 0. При этом путь подготовки тормозов 
Вторую точку возьмем для скорости v = 100 км/ч:
 ;
;
 с;
с;
 м.
м.
Проводим по двум точкам линию 1 на рисунке 8.
 |
Затем из точки на оси абсцисс, соответствующей расстоянию 600 м, в обратном направлении последовательно от v = 0 до пересечения с линией 1 строим кривую скорости 2, соответствующую режиму экстренного торможения. Построение можно выполнить графическим методом Липеца либо по результатам аналитического, либо численного интегрирования уравнения движения поезда. Точка A пересечения линий 1 и 2 соответствует началу отсчета действительного тормозного пути s д и скорости начала торможения
 км/ч.
км/ч.
Таким образом, если рассмотренный выше поезд на спуске крутизной 5 ‰ начнет экстренное торможение при скорости  км/ч, то, пройдя путь подготовки тормозов
км/ч, то, пройдя путь подготовки тормозов  и действительный тормозной путь
и действительный тормозной путь  он остановится на расстоянии 600 м от места поворота ручки крана машиниста в тормозное положение. При скорости начала торможения большей, чем скорость в точке A на рисунке 8, тормозной путь будет больше 600 м.
он остановится на расстоянии 600 м от места поворота ручки крана машиниста в тормозное положение. При скорости начала торможения большей, чем скорость в точке A на рисунке 8, тормозной путь будет больше 600 м.
На практике часто требуется для любого спуска на рассматриваемом участке определить предельно допустимое значение скорости движения поезда, при котором длина тормозного пути не превысит некоторое заданное значение. Иначе говоря, требуется определить ограничение скорости по тормозным средствам для любого из спусков на рассматриваемом участке. В этом случае обычно решают задачу, аналогичную рассмотренной в примере 7, но для трех (двух) значений уклона. В качестве этих уклонов можно принять прямой горизонтальный участок пути (i = 0), наибольший спуск и средний по величине уклона спуск. По полученным трем значениям скорости строят графическую зависимость v доп(i). Пользуясь этой графической зависимостью, находят ограничение допустимой скорости движения поезда по тормозам для любого, встречающегося на рассматриваемом участке спуска.

Пример 8. Определить ограничение скорости движения поезда по тормозам на участке, где наибольший спуск i = –12 ‰. Длина тормозного пути 1200 м. Масса состава Q = 4450 т. В составе 52 четырехосных вагона. Тормозные колодки стандартные чугунные. Диаграмма удельных замедляющих сил для режима экстренного торможения приведена на рисунке 9.
Решение. Количество осей в составе
 осей.
осей.
Значение расчетного тормозного коэффициента при K р= 70 кН/ось
 .
.
Рассчитаем длину пути подготовки тормозов для уклонов 0 ‰, – 6 ‰ и – 12 ‰. Принимая для v = 100 км/ч  (см. пример 7), время подготовки тормозов определим по формуле (38):
(см. пример 7), время подготовки тормозов определим по формуле (38):
для i = 0
 с;
с;
для i = – 6 ‰
 c;
c;
для i = – 12 ‰
 c.
c.
Значения пути подготовки тормозов по формуле (36):
для i = 0
 м;
м;
для i = – 6 ‰
 м;
м;
для i = – 12 ‰
 м.
м.
Эти значения отложим по горизонтали на уровне, соответствующем скорости v = 100 км/ч. Соединим полученные точки с началом координат, построив тем самым линии, по которым изменяется значение s п в зависимости от скорости начала торможения для трех значений уклонов. Из точки, соответствующей заданному значению тормозного пути (s = 1200 м), в обратном направлении строим кривые скорости для режима экстренного торможения на уклонах i, равных 0, –6, –12 ‰. Точки пересечения линий, соответствующих одинаковым уклонам и дают значения предельно допустимой скорости движения для этих уклонов. Так для i = 0 ‰ v д = 97 км/ч, для i = – 6 ‰ v д = 88 км/ч и для i = – 12 ‰ v д = 80 км/ч. Используя полученные значения, строим зависимость v д (i), по которой для любого спуска от i = 0 ‰ до i = – 12 ‰ можно определить ограничение скорости движения поезда по тормозным средствам.
Выше рассмотрены примеры тормозных задач, в условии которых задана обеспеченность поезда тормозами. Задачи второй группы, подразумевающие определение необходимых тормозных средств решают, сводя их к задачам первой группы, что рассмотрим на примере.
Пример 9. Определить достаточно ли тормозных средств у поезда для реализации скорости 80 км/ч на спуске i = –10 ‰ при длине тормозного пути s т = 1200 м. Масса локомотива P = 276 т, состава Q = 4300 т. Все вагоны четырехосные на роликовых подшипниках. Средняя осевая нагрузка вагонов q o = 17 т/ось, все оси тормозные, а тормозное нажатие K р = 70 кН/ось.
Решение. Задаемся четырьмя значениями расчетного тормозного коэффициента Jр1 = 2; Jр2 = 3; Jр3 = 4; Jр4 = 5. Для каждого из принятых значений Jр находим удельные замедляющие силы в зависимости от скорости движения поезда и результаты вычислений сводим в таблицу 10.
Далее решение задачи сводится к четырехкратному решению тормозной задачи первой группы. Для каждого из принятых четырех значений Jр решают задачу, аналогичную рассм