Производство с двумя факторами. Производственная функция

Соотношение между любым набором факторов произ­водства и максимально возможным объемом продукции, производимым из этого набора факторов, описывается про­изводственной функцией. Производственная функция стро­ится для данной технологии. Улучшение технологии увели­чивает максимально достижимый объем выпускаемой про­дукции при любой комбинации факторов и, следовательно, отражается новой производственной функцией. Производ­ственная функция может использоваться для определения минимального количества затрат, необходимого для произ­водства любого данного объема товаров. Производственная функция может быть представлена следующим образом:

Q = f (L,K, M),

где Q - максимальный объем продукции, производимой при данной технологии и данном соотношении труда (L), капи­тала (К) и материалов (М).

Производственная функция может быть изображена графически, если откладывать величину капитала, измеряемую в часах работы машин, вдоль вертикальной оси координат, а труд, также измеряемый в часах, - по горизонтальной оси координат. Каждая комбинация рабочих часов и часов работы машин на графике соответствует определенному объему производства или выпуска. Кривая, отображающая все различные варианты комбинаций ресурсов, которые могут быть использованы для производства данного объема продукции, называется изоквантой.

Изокванта показывает, что существует много вариантов для производства данного объема продукции. Карта изоквант – это ряд изоквант, отражающий максимально достижимый выпуск продукции при любом данном наборе факторов производства. Изокванты имеют форму выпуклых (относительно начала координат) кривых (рис 7), что означает, что вдоль данной изокванты сокращение потребляемых часов труда требует увеличения часов работы машин, чтобы не допустить сокращения производства.

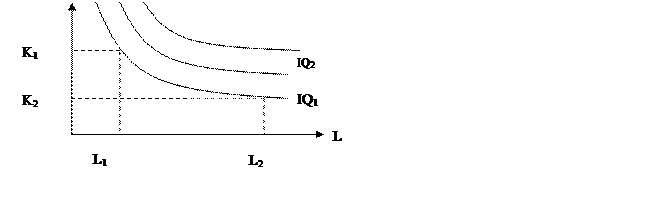
Рис. 7. Карта изоквант

Анализ изоквант можно использовать для определения возможности замещения одного фактора производства другим в процессе их использования. Предельная норма технологического замещения трудом капитала MRTC_LK определяется величиной капитала, которую может заменить каждая единица труда, не вызывая изменения объемов производства.

MRTC_LK = - (Δ L/ Δ К) = МР_L / МР_K

С производственной функцией связа­на функция издержек. Минимизация затрат для производства любого данного объема продукции зависит отчасти от производства максимально возможного объема продукции при данной комбинации факторов.

Если предположить, что используется только два переменных фактора - труд и капитал, то совокупные издержки (ТС) ис­пользования какого-либо количества обоих этих факторов составят:

TC = P_L L + Рк К,

где L измеряется в часах труда, К - в часах работы машин; P_L - почасовая оплата труда; Рк - почасовая величина арендной платы за машины (то есть Рl и Рк - цены использования труда и капитала). Тогда линия, отражающая сочетания затрат труда и капитала, при которых издержки производства рав­ны, будет называться изокостой. Для всех комбинаций факторов, соответствующих линии изокосты, общая величина издержек (ТС) одинакова. На рис. 8 изображено семейство изокост. Чем дальше изокоста от начала координат, тем больший объем ресурсов используется для производства данного объема продукции, и издержки растут. Отношение цен затрачиваемых факторов равно наклону линии изокосты, взятому с отрицательным знаком.

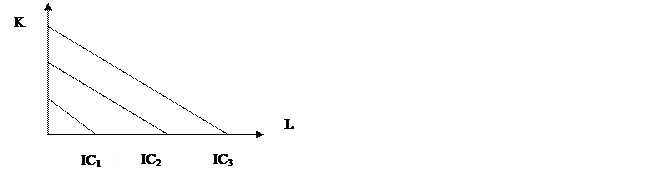
Рис. 8 – Карта изокост

Какую комбинацию ресурсов выберет производитель, чтобы выйти на какую-либо из точек на функции издержек? Ответ на этот вопрос можно получить, совместив карту изоквант (см. рис.6) и семейство изокост для данного произ­водства в одной системе координат (рис.9).

Рис. 9. Взаимосвязь изоквант и изокост

Минимум издержек производства данного объема про­дукции достигается при сочетании рассматриваемых факто­ров производства, соответствующем точке А - точке каса­ния изокванты с линией изокосты, где наклон изокванты для двух видов ресурсов равен наклону изокосты для этих ресур­сов.

Наклон изокванты равен предельной норме технологи­ческого замещения трудом капитала, взятой с отрицатель­ным знаком. Наклон изокосты равен отношению цены труда к цене капитала, взятому с отрицательным знаком. Отсюда следует, что в равновесии МР_L /МРк = Р_L/Рк.

Данное уравнение определяет условие производства любого заданного объема продукции с минимальными за­тратами. Его можно записать следующим образом:

МР_L/ Р_L = МРк /Рк.

Это запись принципа наименьших затрат: равные пре­дельные продукты факторов производства на рубль затрат. При выполнении этого условия можно говорить, что произ­водитель добивается максимально возможного выпуска объ­ема продукции при заданных затратах.