Два элемента подобны, если характеристики одного могут быть получены путем пересчета характеристик другого.
Различают абсолютное и практическое подобие. Первое требует тождества всех процессов в объектах в пространстве и во времени. Второе же требует подобия только тех процессов, которые существенны для данного исследования.
Теория подобия нашла широкое применение, как средство, значительно уменьшающее трудовые и материальные затраты, сокращающее сроки проектирования и внедрение объектов в производство, позволяющее выбирать оптимальные (рациональные) значения геометрических, силовых и других параметров машин.
Более ста пятидесяти лет назад возникла новое направление научного знания – учение о подобие. В 1686 г. И.Ньютоном было высказано гениальное предвидение, а в 1848 г. Ж.Бертраном была сформулирована первая теорема подобия для механических систем о существовании инвариантов подобия. Исходя из математического выражения второго закона Ньютона, Бертран показал, что у подобных явлений есть комплекс, имеющий одно и то же значение в сходственных точках подобных явлений. Этот комплекс называется инвариантом, или критерием механического подобия.
В общем случае различают три вида подобия: геометрическое, кинематическое и динамическое. Наиболее простым является подобие геометрическое, требующее, чтобы линейные размеры натуры и модели находились в постоянном соотношении, другими словами, модель повторяет натуру в каком-то масштабе.
Это требование можно записать в виде
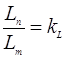
где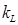 
- масштабный множитель.
Для площадей (S) и объемов (V)
; 
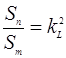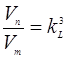
Применительно к физическим явлениям элементарные представления геометрического подобия расширяются и распространяются на все величины, характеризующие данный процесс. Если учесть, что они могут изменяться как во времени, так и в пространстве, образуя поля, то возникает понятие о временном подобии и подобии полей, называемое кинематическим подобием.
В механике жидкости оно сводится к подобию полей скоростей в потоках, движущихся в геометрически подобных каналах.
И наконец, имея в виду, что механическое движение происходит под действием сил, вводится понятие динамического подобия, которое требует, чтобы в соответствующих точках натуры и модели силы находились в постоянном соотношении.
Рассмотрим простейший пример. Известно, что движение любой механической системы подчиняется закону Ньютона
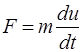(2.1)
Для двух подобных систем можно записать
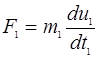и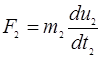 
Разделив первое на второе получим:
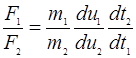либо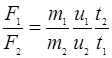 
Имея в виду, что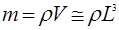 
имеем
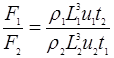
По смыслу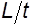 
есть скорость, поэтому
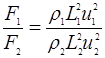(2.2)
либо
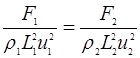(2.3)
Очевидно, что полученные комплексы безразмерны.
Таким образом, для двух подобных систем сохраняется числовое равенство безразмерных комплексов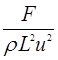 
. Кратко это условие можно записать так: 
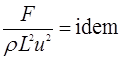. В честь Ньютона этот комплекс обозначается двумя первыми буквами его фамилии, т.е.
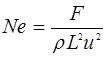(2.4)
и называют числом подобия Ньютона, а выражение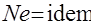 
- основным законом динамического подобия механических систем (законом Ньютона).
Величины L и u, входящие в (2.4), называются определяющим линейным размером и определяющей скоростью. При проведении опытов они выбираются экспериментатором произвольно, исходя из удобства их измерения.
Полученные результаты заслуживают того, чтобы остановиться и сделать кое-какие полезные выводы. Во-первых, они позволяют ответить на один из поставленных выше вопросов: как спроектировать и построить модель. Ответ очевиден: так, чтобы она была геометрически подобна натуре.
Во-вторых, из сказанного следует, что для обеспечения динамического подобия не требуется, чтобы все величины, определяющие характер процесса в натурном объекте, были численно равны аналогичным величинам в модели. Достаточным является равенство безразмерных комплексов, составленных из этих величин для натуры и модели, называемых инвариантами подобия.
Какие преимущества дает такой подход в практическом плане?
Из математической статистики известно, что число опытов, которое необходимо поставить для того, чтобы получить закономерность, достоверно описывающую какое-то физическое явление, определяется из соотношения:
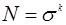(2.5)
где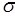 
- число экспериментальных точек, которое необходимо снять для обеспечения представительности опыта (
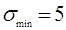); k - число величин, подлежащих варьированию в опытах.
Таким образом, минимальное число опытов
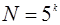(2.6)
Если в опытах варьируется число Ньютона (например, за счет изменения скорости), то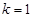 
и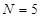 
, но если изучать влияние каждой из величин (
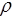, u, L), то 
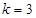и число опытов 
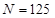. Следовательно, использование числа подобия в качестве своеобразной «обобщенной переменной» позволяет уменьшить число необходимых опытов в 25 раз, а если для надежности принять 
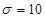, то в 100 раз.
И наконец, в-третьих, можно ответить на вопрос о том, какие величины следует измерять в опытах и как переносить результаты на натурный объект. Так как при проведении опытов необходимо обеспечить равенство чисел подобия натуры и модели, то ясно, что измерению подлежат лишь те величины, которые входят в эти числа.
По результатам измерений можно вычислить числа подобия модели и, исходя из равенства их числам подобия натуры, произвести пересчет.
Остается открытым вопрос, который, по существу, является центральным. Как же найти числа подобия, характеризующие изучаемый процесс либо явление? Очевидно, что только ответ на него открывает путь для практической реализации теории подобия.
Ответ на этот вопрос дают основные теоремы подобия.
В природе существуют только те подобные явления, у которых критерии одинаковы. Это и есть первая теорема подобия, которая носит имена Ньютона и Бертрана. Для явлений, подобных в том или ином смысле, существуют одинаковые критерии подобия.
Тотчас после вывода началось практическое применение первой теоремы для обработки опытных данных в так называемых критериях подобия. О.Рейнольдс выразил закон движения жидкости по трубам одной общей формулой, названной впоследствии критерием Рейнольдса. Оказалось возможным объединить таким путем все численные данные опытов по гидравлическому сопротивлению, проведенными различными исследователями на воде, воздухе, паре, различных маслах и т.д. Фруд, изучая мореходные качества судов на моделях, представил результаты опытов в виде критериального уравнения, которые можно было распространить на суда, подобные по своей геометрической конфигурации испытанным моделям. Выдающийся русский ученый Н.Е.Жуковский положил теорию подобия в основу критериальной обработки опытов над моделями самолетов, продуваемых в аэродинамической трубе, для того, чтобы результаты опытов можно было перевести на подобные моделям самолеты.
Если бы уравнение физического процесса можно было составить из инвариантов подобия, то это было бы общее уравнение, одинаковое для всех подобных явлений.
Вторая теорема подобия устанавливает возможность такого преобразования физических уравнений и носит имя американского ученого Букингэма. Полное уравнение физического процесса может быть представлено зависимостью между критериями подобия, т.е. зависимостью между безразмерными величинами, определенным образом полученными из уравнения процесса.
Первая и вторая теоремы были выведены из предположения, что подобие явлений уже установленный факт. Обе теоремы устанавливают свойства подобных явлений, но они не указывают способа для определения подобия этих явлений. Возникает вопрос: по каким признакам можно определить подобие явлений?
Ответ дает третья теорема подобия, которая носит имена М.В.Кирпичева и А.А.Гухмана: необходимыми и достаточными условиями для создания подобия является пропорциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия сопоставляемых явлений. К условиям однозначности относятся следующие, не зависящие от механизма самого явления:
· геометрические свойства системы, в которой протекает процесс;
· физические параметры среды и тел, образующих систему;
· начальное состояние системы (начальные условия);
· условия на границах системы (граничные или краевые условия);
· взаимодействие объекта и внешней среды.
Процессы в объекте исследования описываются в общем случае системой дифференциальных уравнений связи между факторами и параметром. Необходимым условием подобия двух объектов является одинаковый вид системы уравнений. Только в этом случае характер процессов в объектах может быть одинаковым и их можно отнести к одному классу. Подобие кроме сходства систем уравнений предъявляет к объектам требования однозначности.
3.3. Критерии подобия, π – теорема
Критерии подобия – безразмерные комбинации, которые составлены из физических величин, описывающих процессы в исследуемых объектах.
Принято обозначать критерии подобия буквой π. В соответствии с теорией подобия при экспериментах необходимо измерять все величины, входящие в критерий. Обрабатывать результаты следует в виде зависимостей между критериями подобия. Полученные таким образом зависимости будут справедливы не только для данного эксперимента, но и для всех подобных объектов.
Вторую теорему подобия часто называют π – теоремой. Однако π -теорема является более информативной и имеет прикладной характер.
В соответствии с π -теоремой, если процесс в объекте характеризуется m фундаментальными физическими величинами, для выражения размерностей которых используется k основных единиц, то этот процесс можно описать m-k безразмерными комбинациями, составленными из этих величин.
Из теоремы следуют два важных практических вывода:
первый – уравнения, описывающие физические процессы, могут быть выражены уравнениями связи между безразмерными комбинациями – критериями подобия. Последние уравнения будут справедливы для всех подобных объектов.
второй - число независимых критериев равно m-k. Оно меньше числа размерных физических переменных на число основных единиц. Т.е. речь идет об уменьшении числа переменных, которыми описывают процесс. Это в свою очередь ведет к уменьшению объема экспериментальных исследований и делает результаты более наглядными.