Применение гиперболических моделей

Модель нелинейна по переменным.

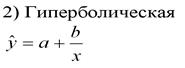
Полиномиальная.

Применение полиномиальных моделей.

Полиномом второй степени могут быть представлены зависимости:

ü Заработная плата физического труда от возраста

ü Урожайность от количества внесенных удобрений

ü Прибыль от количества каналов, исполняющих заявки в системе массового обслуживания и т.д.

Применение гиперболических моделей

Классический пример: кривая Филлипса - графическое отображение обратной зависимости между уровнем инфляции и уровнем безработицы

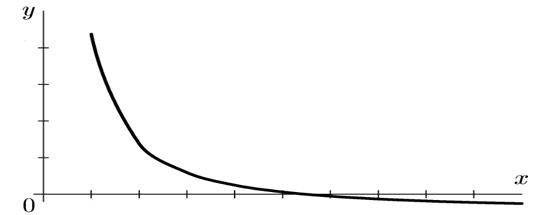
Х – общий уровень безработицы (в процентах)

Y – годовой темп прироста ставки заработной платы (в процентах )

Так, для кривой Филлипса— величина параметра а, равная 0,00679, означает, что с ростом уровня безработицы темп прироста заработной платы в пределе стремится к нулю. Соответственно можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.

Пример произвольной логарифмической модели.

Может быть использована для описания доли расходов на товары длительного пользования (кривая Энгеля) в зависимости от общих сумм расходов.

Если модель нелинейна по переменным, то введением новых переменных такую модель можно свести к линейной, для оценки параметров которой используется обычный метод наименьших квадратов.

Рассмотрим примеры линеаризующих преобразований:

1) Полиномиальная модель: .

 

Соответствующая линейная модель: , где .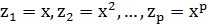

Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничения в применении полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно меньше однородность совокупности по результативному признаку.

Парабола второй степени целесообразна к применению, если определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь изменяется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени:

Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:

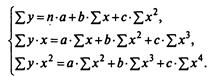
Решить ее относительно параметров а, b, с можно методом определителей:

При b > 0 и с < 0 кривая симметрична относительно высшей точки, т. е. точки перелома кривой, изменяющей направление связи, а именно рост на падение. Такого рода функцию можно наблюдать в экономике труда при изучении зависимости заработной платы работников физического труда от возраста — с увеличением возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы работника. Если параболическая форма связи демонстрирует сначала рост, а затем снижение уровня значений результативного признака, то определяется значение фактора, при котором достигается максимум. Так, предполагаем, что потребление товара А (единиц) в зависимости от уровня дохода семьи (тыс. руб.) характеризуется уравнением вида Приравнивая к нулю первую производную , найдем величину дохода, при которой потребление максимально, т. е. при х = 3 тыс. руб.

При b < 0 и с > 0 парабола второго порядка симметрична относительно своего минимума, что позволяет определять минимум функции в точке, меняющей направление связи, т. е. снижение на рост. Так, если в зависимости от объема выпуска продукции затраты на производство характеризуются уравнением то наименьшие затраты достигаются при выпуске продукции х = 15 ед., т. е. —60 + 2 • 2 • х = 0.

 

2) Гиперболическая модель: .

Соответствующая линейная модель: , где .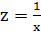

Оценка параметров которого может быть дана МНК. Система нормальных уравнений имеет вид:

 

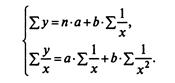
При b>0 имеем обратную зависимость, которая при х характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр а.(Кривая Филипса).

При b <0 имеем медленно повышающуюся функцию с верхней асимптотой при х , т. е. с максимальным предельным уровнем у, оценку которого в уравнении дает параметр а. Примером может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Математическое описание подобного рода взаимосвязей получило название кривые Энгеля, В 1857 г. немецкий статистик Э. Энгель на основе исследования семейных расходов сформулировал закономерность — с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается. Соответственно с увеличением дохода доля расходов на непродовольственные товары будет возрастать. Однако этот рост не беспределен, ибо сумма долей на все товары не может быть больше единицы, или 100%, а на отдельные непродовольственные товары данный предел может соответствовать величине параметра а для уравнения вида

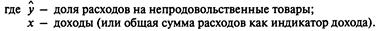
Вместе с тем равносторонняя гипербола не является единственно возможной функцией для описания кривой Энгеля. В 1943 г. Уоркинг и в 1964 г. С. Лизер для этих целей применили полулогарифмическую кривую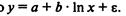

Заменив In х на z, вновь получим линейное уравнение 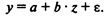Данная функция, как и предыдущая, линейна по параметрам и нелинейна по объясняющей переменной х. Оценка параметров а и b может быть найдена МНК. Система нормальных уравнений при этом имеет вид:

 

 

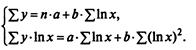
3) Логарифмическая модель: .

Соответствующая линейная модель: , где .

 

Применяя МНК, получаем формулы для расчета параметров модели:

Возможны и иные модели, нелинейные по объясняющим переменным. Например, Соответственно система нормальных уравнений для оценки параметров имеет вид:

Уравнения, в которые входят применялись в исследованиях урожайности, трудоемкости сельскохозяйственного производства. Уравнения такого рода легко линеаризуются путем замены на z.

Следует отметить и недостаток такой замены переменных, связанный с тем, что вектор оценок получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же.

 

2.Регрессии, нелинейные относительно параметров.

Модели нелинейные по параметрам. Среди таких моделей выделяют нелинейные модели внутренне линейные и нелинейные модели, внутренне нелинейные. Модели внутренне линейные можно привести к линейному виду с помощью соответствующих преобразований.

 

Примеры внутренне линейных моделей и их линеаризация:

1) Мультипликативная степенная модель: .

Линеаризующее преобразование:

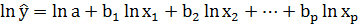
или

,

где .

2) Экспоненциальная модель: .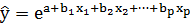

Линеаризующее преобразование: .

3) Обратная регрессионная модель: .

Линеаризующее преобразование: .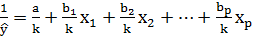

Если нелинейная модель внутренне линейна, то с помощью соответствующих преобразований она может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цены широко используется степенная функция.

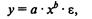
Внутренне нелинейной будет и модель вида:

потому что эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам.

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция . Это связано с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. является коэффициентом эластичности. Это значит,что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %. Так, если зависимость спроса от цен характеризуется уравнением вида то, следовательно, с увеличением цен на 1 % спрос снижается в среднем на 1,12 %.

Для оценки параметров степенной функции 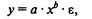применяется МНК к линеаризованному уравнению lny= lna+b*lnx+lne, т.е. решается система нормальных уравнений:

В отдельных случаях применяется и нелинейная модель вида

так называемая обратная модель, являющаяся разновидностью гиперболы.

 

В качестве примера использования линеаризирующего преобразования регрессии рассмотрим производствееную фенкцию Кобба-Дугласа.

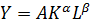
Где Y-объем производства,K- затраты капитала,L-затраты труда.

Показатели являются коэффициентами частной эластичности объема производства Y соответственно по затратам капитала К и труда L. Это означает,что при увеличении одних только затрат капитала(труда)на 1% объем производства увеличится на .

Учитывая влияние случайных возмущений присущих каждому экономическому явлению, функция Кобба-Дугласа можно представить в виде

.(1)

Полученную мультипликативную модель легко свести к линейной путем логарифмирования обеих частей уравнения. Тогда для i-го наблюдения получим:

lny=lnA+ lnK+ 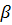lnL+ln .

 

Если в модели 1 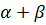=1(т.е модель такова, что при расширении масштаба производства-увеличение затрат капитала K и труда L в некоторое число раз- обем производства возрастает в то же число раз) функцию Кобба –Дугласа представляют в виде

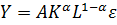или

Таким образом,получаем зависимость производительности труда()от ео капиталовооруженности (K/L). Для оценки параметров модели путем логарифмирования приводим ее к виду

ln(Y/L)=lnA+ ln(K/L)+ln

Функция Кобба –дугласа с учетом технического прогресса имеет вид:

Где t- время, параметр - темп прироста объема производства благодаря техническому прогрессу. Модель приводится к линейному виду анологично модели (1).