Понятие и оценка денежного потока

Одной из важнейших задач финансового менеджмента является оценка денежного потока С₁, С₂, …, С_n, генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта или функционирования актива. Элементы потока С_i могут быть как независимыми, так и связанными между собой определенным алгоритмом. Если поступления имеют место в начале периода, то поток называют поток пренумерандо, если в конце, – поток постнумерандо. Поток постнумерандо на практике встречается чаще всего.

Оценка денежного потока может выполняться в рамках решения двух задач:

1) прямой задачи (схема наращения), предполагающей оценку наращенного денежного потока, т.е. в основе ее лежит будущая стоимость;

2) обратной задачи (схема дисконтирования), предполагающей суммарную оценку дисконтированного (приведенного) денежного потока; поскольку отдельные элементы денежного потока генерируются в различные периоды времени и деньги имеют временную ценность, постольку непосредственное их суммирование невозможно и осуществляется приведение денежного потока к одному моменту времени.

Рассмотрим наиболее распространенную ситуацию, когда денежные поступления по годам варьируют. Пусть С₁, С₂, …, С_n –денежный поток, r – ставка дисконтирования. Требуется найти стоимость данного денежного потока с позиции будущего и с позиции настоящего.

Прямая задача. Если на первое денежное поступление С₁ начисляются сложные проценты за период (n- 1 ), то в конце n-го периода оно станет равным C₁( 1 +r)^{n- 1}. На второе денежное поступление С₂ начисляются сложные проценты за период (n- 2) и оно станет равным С₂( 1 +r)^{n- 2} и т.д. Наращенный денежный поток для исходного потока имеет следующий вид: C₁( 1 +r)^{n- 1}, С₂( 1 +r)^{n- 2}, С_n-1( 1 +r), C_n. Иначе, будущую стоимость исходного денежного потока можно представить в виде

FV = 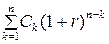. (2.13)

Обратная задача. Рассуждая по аналогии с изложенным для прямой задачи, получим приведенный денежный поток для исходного потока: С₁/( 1 +r), C₂/( 1 +r) ², …, C_n/( 1 +r)ⁿ. Или иначе, приведенная стоимость денежного потока имеет вид

PV = . (2.14)

Чистую приведенную стоимость денежного потока при этом можно рассчитать по формуле

NPV = C₀ + . (2.15)

В общем случае процентные ставки могут быть различными для каждого из будущих периодов. Связь между процентной ставкой и временем поступления денежных средств называется временной структурой процентных ставок.

Оценка аннуитетов

В качестве общего случая обычно рассматривается денежный поток, не предполагающий равенства элементов, относящихся к разным периодам. Однако некоторые частные случаи денежного потока представляют особый интерес и часто используются в финансовых вычислениях. Наиболее популярными являются аннуитеты. Аннуитет, или финансовая рента, представляет собой актив, который приносит фиксированный доход ежегодно в течение определенного ряда лет. Если период, в течение которого предполагается выплата фиксированного дохода, не ограничен, то мы имеем дело с бессрочной рентой. Примером бессрочной ренты можно считать облигации британского правительства, по которым оно не берет обязательств погашения, но предлагает ежегодный фиксированный доход в течение неограниченного периода. Норма доходности таких ценных бумаг равна обещанным годовым выплатам C, деленным на их приведенную стоимость:

r = C/PV. (2.20)

Для доказательства в формулу приведенной стоимости бессрочной ренты

PV = C/( 1 +r) + C/( 1 +r) ² + C/( 1 +r) ³ + …

введем обозначения: a = C/( 1 +r) и x = 1 /( 1 +r). Тогда PV = a( 1 + x + x ² +…). Умножаем обе части на х и получаем: PV x = a(x + x ² + …). Вычитая это выражение из предыдущего, получаем PV( 1 -x) = a. Подставим значения а и х и умножим обе части на (1+ r). Получим r = C/PV. Следовательно, приведенная стоимость бессрочной ренты равна:

PV = C/r. (2.21)

Интересным случаем бессрочной ренты является возрастающая бессрочная рента. Она имеет место, если денежный поток от периода к периоду возрастает на один и тот же процент: С₁, C₂=C₁ (1+ g), C₃=C₁ (1+ g)² и т.д. Рассуждая по аналогии со случаем обычной бессрочной ренты, можно показать, что приведенная стоимость возрастающей бессрочной ренты равна:

PV = + … = С₁/(r-g). (2.22)

Стандартный же аннуитет предполагает конечное число лет получения фиксированного дохода от актива. Несложно заметить, что аннуитет в виде регулярных платежей в период с 1-го года по n -ый год равен разнице между двумя бессрочными рентами (рис. 2.3). Приведенная стоимость бессрочной ренты, которая дает ежегодно поток денежных средств C, начиная с года (n+ 1), равна С/r. Следовательно, сегодня ее приведенная стоимость равна:

.

Поскольку аннуитет С за n лет представляет собой разницу между бессрочной рентой, платежи по которой начинаются в первом году, и бессрочной рентой, платежи по которой начинаются в году (n+ 1), то приведенная стоимость этого аннуитета равна разнице между приведенными стоимостями этих двух бессрочных рент:

= С × FM4(r,n). (2.23)

Рис. 2.3. Аннуитет как разница между двумя бессрочными рентами

Дисконтирующий множитель FM4(r,n) – это коэффициент аннуитета, который представляет собой приведенную стоимость со ставкой дисконтирования r аннуитета в одну денежную единицу, выплачиваемого в конце каждого периода t. Его значения для конкретных r и n можно найти при помощи финансовых таблиц или финансового калькулятора.

Текущая стоимость аннуитета находит применение при так называемом погашении ссуды в рассрочку (методе депозитной книжки). При этом предполагается, что взятая ссуда погашается ежегодно равными платежами, включающими как проценты, так и выплату основной суммы долга.

П р и м е р. В банке получена ссуда в размере 10 000 рублей на 5 лет под 15% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Предполагается возвращать ссуду равными суммами в конце каждого года. Задача при этом состоит в определении размера годового платежа.

Инвестируя 10 000 рублей, банк фактически приобретает аннуитет. Проценты, предполагающиеся к получению в конце первого года использования заемщиком ссуды, составят 1500 рублей. Кроме процентов, общий платеж в конце первого года будет включать также (С -1500) руб., где С – это размер аннуитета. В конце следующего года сумма выплачиваемых процентов уменьшится (поскольку проценты начисляются на непогашенный остаток), а сумма, идущая в погашении основного долга, увеличится так, чтобы общая величина платежа снова равнялась С. Таким образом, мы имеем дело с аннуитетом, текущая стоимость, ставка и продолжительность которого равны соответственно размеру, процентной ставке и длительности ссуды:

10 000 = С×FM4 (15,5) = С ×3,352, т.е. С = 2 983 (руб.).

Схема платежей (руб.) при этом будет выглядеть следующим образом:

Контрольные вопросы