Для расчета калькулятора

Задание:

Используя экспериментальные данные по адсорбции и десорбции гексана (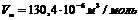, 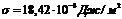) на силикагеле при Т=293 К, выполните следующие задания:

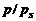
		0,15	0,25	0,4	0,45	0,5
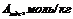
		0,6	1,1	2,0	2,7	3,6
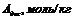
		0,6	1,1	2,0	2,9	4,9

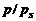
	0,55	0,6	0,65	0,7	0,75	0,8
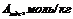
	4,6	5,9	7,4	8,6	9,8	10,1
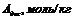
	6,4	7,5	8,5	9,2	9,8	10,1

1. Постройте изотерму капиллярной конденсации.

2. Вычислите предельный объем пор адсорбата, используя в расчетах точки кривой адсорбции.

3. Используя экспериментальные точки кривой десорбции газа, рассчитайте и постройте интегральную и дифференциальную кривые распределения пор по размерам. Определите основной размер пор данного адсорбента.

4. Проанализируйте полученные результаты.

Решение:

1. По экспериментальным данным строим изотермы адсорбции и десорбции:

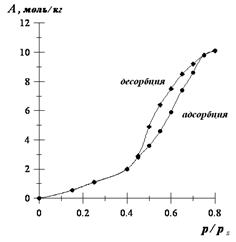
Рис.13. Изотермы адсорбции и десорбции гексана на силикагеле.

2. Для расчета предельного объема пор силикагеля ():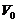

а) Рассчитаем адсорбционный потенциал адсорбата для относительного давления р/р_S =0,15 по уравнению (7):

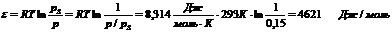
Аналогичный расчет проведем для других значений р/р_S, рассчитанные значения адсорбционных потенциалов занесем в таблицу:

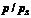
	0,15	0,25	0,4	0,45	0,5	0,55

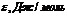
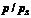
	0,6	0,65	0,7	0,75	0,8

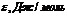
б) Рассчитаем адсорбционный объем (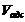) по уравнению (6). Расчет ведем по изотерме адсорбции А_адс = 0,6 моль/кг.

.

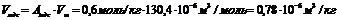Аналогичный расчет проведем для других значений А_адс, рассчитанные значения адсорбционных объемов занесем в таблицу:

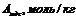
	0,6	1,1	2,0	2,7	3,6	4,6

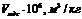
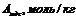
	5,9	7,4	8,6	9,8	10,1

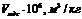
в) Прологарифмируем полученные значения 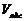. Рассчитанные значения 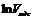занесем в таблицу.

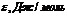
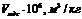
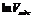
	-9,45	-8,85	-8,25	-7,95	-7,66	-7,4

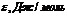
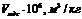
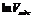
	-7,17	-6,94	-6,79	-6,66	-6,63

Строим прямую в координатах .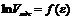

Рис.14. Линейная зависимость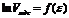

Из рис.14 следует, что 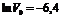, следовательно, предельный объем пор силикагеля составляет: .

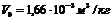3. Для построения интегральной кривой распределения пор по размерам рассчитаем объем и радиус пор по данным десорбции гексана с поверхности силикагеля. Расчет ведем по уравнениям (6) и (10) для А_дес = 0,6 моль/кг и ε = 4621 Дж/моль.

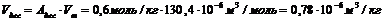
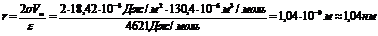
Аналогичный расчет проведем для других значений А_дес и ε, рассчитанные значения адсорбционных объемов и радиусов пор занесем в таблицу:

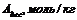
	0,6	1,1	2,0	2,9	4,9	6,4
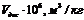
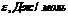
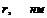
	1,04	1,42	2,15	2,47	2,84	3,30

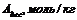
	7,5	8,5	9,2	9,8	10,1
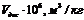
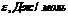
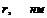
	3,86	4,56	5,53	6,85	8,82

По рассчитанным данным строим интегральную кривую распределения пор по радиусам в координатах :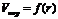

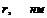
	1,04	1,42	2,15	2,47	2,84	3,30

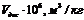
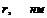
	3,86	4,56	5,53	6,85	8,82

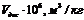
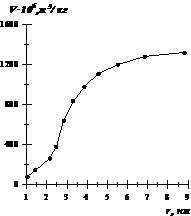
Рис.15. Интегральная кривая распределения пор силикагеля по размерам

4. Для построения дифференциальной кривой распределения пор по размерам продифференцируем интегральную кривую распределения:

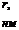
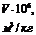
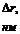
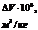
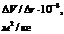
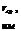
1,04
1,42		0,40			1,23
2,15		0,73			1,79
2,47		0,32			2,31
2,84		0,37			2,66
3,30		0,46			3,07
3,86		0,56			3,58
4,56		0,70			4,21
5,53		0,97			5,05
6,85		1,32			6,19
8,82		1,97			7,84

Используя данные таблицы, строим дифференциальную кривую распределения пор по радиусам в координатах :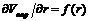

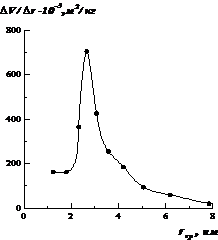
Рис.16. Дифференциальная кривая распределения пор силикагеля по размерам.

Из рис.16 следует, что поры данного силикагеля, в основном, имеют размер порядка 3 нм, следовательно, данный адсорбент относится к мезопористым.

Пример выполнения задания с использованием для