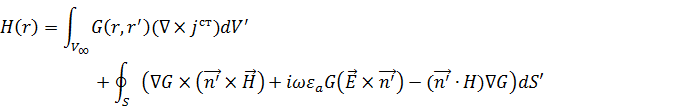Интегральные представления
Пусть имеется объект 
с границей 
и внешней областью 
(граница 
) с расположенными в ней сторонними возбуждающими токами 
.
В области 
волновая функция 
удовлетворяет уравнению Гельмгольца
, 
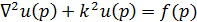(1)
Волновая функция должна удовлетворять условиям излучения
, 
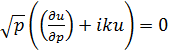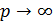
Необходимо получить интегральное представление функции 
в области 
. Функция Грина удовлетворяет уравнениям Гельмгольца
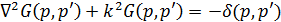, (2)
Для нахождения решения уравнения (1), умножим (1) на 
, а (2) – на ИУ. Выполняем вычитание левых и правых частей и интегрирование полученных выражений по области 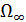. В результате имеем:
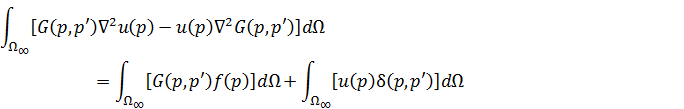
Далее выполняем следующие преобразования:
а). поверхностный интеграл заменим контурным при помощи скалярной теоремы Грина
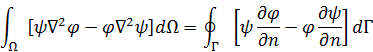
Функции, входящие в интеграл, непрерывны вместе с производными второго порядка везде, вплоть до контура 
, который должен быть главкой по критерию Ляпунова (в каждой точке контура существует нормаль). Поскольку 
, а на выполняется условие излучения, то в контурном интеграле остается интеграл по контуру . Во втором слагаемом справа интеграл дает 
.
Из-за симметрии функции Грина (в функции Грина замена не делается) 
. В итоге получаем
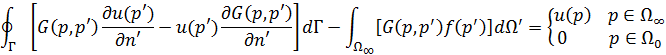
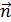– внешняя нормаль по отношению к области , 
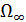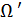- область, где 
.
В результате, для нахождения решения в некоторой области 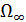необходимо располагать сведениями о его поведении на границе .
В контурный интервал входят 
и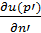 
.
Если – электрическое поле, то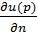 
– магнитное поле. Если объект отсутствует, то
Интегральные уравнения
Интегральные уравнения позволяют получить более компактные выражения, а ГУ учитываются на этапе вывода ИУ.
Двумерный случай:
Металлический объект:
Е-поляризация, ИУ первого рода. Пусть имеется объект 
идеально проводящий,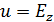 
, выполняется условие излучения. На поверхности металла выполняется ГУ для полного поля:
, 
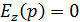Считаем, что для полного поля отсутствует зависимость по 
. Примером такой функции для возбуждающего первичного поля является нить электрического тока 
:
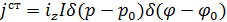
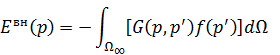
Учитывая 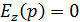при , получаем ИУ первого рода:
,
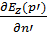- магнитное поле.
На поверхности металла магнитное поле испытывает скачок, пропорциональный поверхностному электрическому току.
Н-поляризация. ИУ второго рода. ГУ:
,
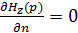Первичное поле возбуждается нитью магнитного тока
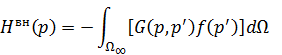
На контуре обращается в ноль производная полного поля.
Для гладких тел можно исключить особенность ядра из ИУ
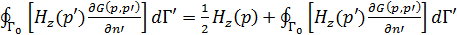(в смысле главного значения)
Интеграл с сильной особенностью заменяется интегралом в смысле главного значения. Особая точка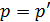 
исключена из области интегрирования в виде выделенного свободного слагаемого.
Получаем ИУ второго рода
Диэлектрический объект
1). Е-поляризация. Двумерные ИУ второго рода.
Пусть объект характеризуется отличной от нуля диэлектрической проницаемостью.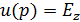 
. Выполняется условие убывания поля на бесконечности и граничные условия для полного поля в виде непрерывности касательных составляющих электрического поля 
и магнитного поля 
(как в предыдущем случае).
Можно подойти по-другому:
,
– постоянная распространения свободного пространства
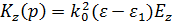– сторонний источник.
Учитывая, что исчезает благодаря выполнению условию излучения, получаем формулу, которая получается в отсутствии объекта
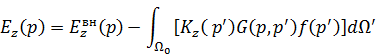
Поле внутри диэлектрика содержится и в свободном члене и под интегралом.
Векторное представление поля в пространстве через функции Грина
В трехмерном случае при наличии только электрические токи называются функциями Стретона - 
.
