Задача 2. Составить матрицу смежности Рис.5.
Пример заполнения см. на сайте www.dgec.mirea.ru “Матрица смежности».
2.2.1. Алгоритм составления матрицы смежности.

Рис.5.
Для полного, непротиворечивого и независимого задания геометрической модели составного тела необходимо использовать матрицу смежности. Это связано с тем, что она обеспечивает возможность организации и воспроизведения процесса моделирования, а также анализа и корректировки модели тела.
Заполнение матрицы смежности осуществляется в порядке формообразования составного геометрического тела и будет, осуществляется в следующей последовательности:
• записывается присвоенный порядковый номер составляющих тел-примитивов в порядке возрастания (придерживаются правила; от внешних к внутренним и от больших к меньшим см. ранее);
• записывается наименование составляющих тел-примитивов;
• выявляется число и геометрический смысл параметров формы составляющих тел-примитивов Pф;
• определяется число и геометрический смысл параметров положения составляющих тел Pп;
• выявляется число и геометрический смысл совпадения параметров формы с параметрами формы других составляющих тел-примитивов, рассмотренных перед ними в матрице смежности Кф;
• выявляется число и геометрический смысл совпадения параметров положения с параметрами положения других составляющих тел-примитивов, рассмотренных перед ними в матрице смежности ранее Кп;
• подсчитывается и записывается итоговое число параметров для каждого тела-примитива, а так же обозначение параметров. Например, для тела примитива № 1 запишем: 3 (b1, c1, h1);
• определяется логическая взаимосвязь составляющих тел-примитивов. Для этого используют булевы операции: объединения (È) и вычитания (/).
Следует помнить, что тела-примитивы, полученные в результате операции вычитания, между собой не взаимодействуют, и соответствующая ячейка матрицы для них не заполняется. (Пустота не может взаимодействовать с пустотой). Например, считается, что цилиндрическое отверстие 6 не взаимодействует с призматическим 7, хотя из рисунка видно, что они пересекаются.
Параметры формы и положения (размеры) вытекают непосредственно из задания. Параметры формы Pф тел-примитивов были определены ранее и указаны на эскизах тел примитивов см. рис. 4.
В соответствии с возможными шестью параметрами положения (три переноса и три поворота относительно осей КСК) выявляются параметры положения заданных тел-примитивов Pп относительно КСК заданного составного геометрического тела.
На рис.7 указаны параметры положения некоторых составляющих тел относительно выбранной системы координат.
Рассмотрим более конкретно некоторые этапы данного алгоритма.
2.2.2. Заполнение матрицы смежности осуществляется в порядке распознавания. То есть согласно присвоенным номерам тел-примитивов (рис. 4). Например, в рассматриваемом задании призма 1 объединяется с цилиндром 2.
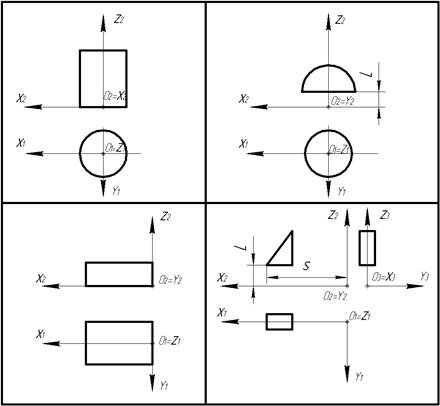
Рис. 6
Для призмы 1: h1 - высота, c1 - ширина и b1 – длина. У неё отсутствуют параметры положения Рп, так как начало её КСК совпадает началом КСК всего тела. Поскольку призма была принята за базовое тело, то у неё отсутствуют коэффициенты совпадения Кф и Кп. Для цилиндра 2 имеем параметры формы Æ2 - диаметр и h2 – высота. У него отсутствуют параметры положения Рп, так как начало его КСК совпадает началом КСК всего тела, но поскольку его параметр формы Æ2 (диаметр) совпадает с параметром базового тела призмы (с её шириной c1), то появляется коэффициент формы Кф, который записывается в соответствующую графу, как Æ2 = c1 и т. д. Так для параллелепипеда (7) параметром положения будет перенос по оси OZ. Для сферы (3) - перенос по оси OZ и т.п.
При определении коэффициентов совпадения и последующей записи их в матрицу смежности следует придерживаться правила: Записывается совпадение “текущего” с ”более ранним”. Например, как было отмечено, у цилиндра 2 его диаметр совпадает с шириной призмы 1 записанной ранее. Поэтому, во второй строчке матрицы смежности, относящейся к этому цилиндру, в графе Кф записали Æ2 = c1, т. е. совпадение “текущего” параметра (в данном случае параметра второго тела-примитива) с ”более ранним” параметром (в данном случае с параметром первого тела-примитива). Справедливости ради следует отметить, что если бы мы в первой строчке, относящейся к призме записали в графе Кф зависимость с1 = Æ2, то во второй строчке (для цилиндра), Кф не надо было указывать и тогда общее количество размеров для простановки осталось бы прежним. Однако в этом случае можно запутаться и несколько раз учесть один и тот же коэффициент. По этому при определении и записи коэффициентов настоятельно рекомендуется придерживаться того правила, что записывается совпадение “текущего” с ”более ранним”.
После определения количества тел-примитивов и их взаимодействия необходимо подготовить соответствующую матрицу смежности. Можно начертить матрицу карандашом на ватмане или выполнить в графической программе Компас. Для этого надо запустить программу «Компас - График». Выберете режим «Файл» => «Создать» => «Чертёж» режим 2D => «ОК». В строке меню указать мышкой на «Сервис» => «Параметры» => выбрать «Текущий чертёж» => «Параметры первого листа» => «Формат». Установить формат А3 и положение «Горизонтально» => «ОК» рис. 7. Сохранить его.

Рис.7
На панели «Обозначение», указываем мышкой на пиктограмме «Ввод таблицы» рис. 8. => Во всплывшем меню устанавливаем требуемое для нашего примера количество столбцов, строк, и соответствующие размеры рис. 9. => «ОК» => «Создать объект» на «Панели свойств» => «STOP».


Рис. 8 Рис. 9
В результате получаем заготовку матрицы рис.10. С помощью команды «Отрезок», «Усечь кривую», и т. д., поменяв стиль линии отрисовки отрезка на «Тонкая», дочерчиваем недостающие элементы матрицы рис. 11. (Если Вы работаете в версии 13, то не забудьте включить угловую привязку, отключённую по умолчанию.)


Рис. 10 Рис. 11
Для заполнения части матрицы, созданной с помощью команды «Ввод таблицы», достаточно кликнуть на ней мышкой. Для заполнения “дорисованной” части справа, используем работу в текстовом редакторе. При этом для точного “попадания” в ячейки таблицы рекомендуется отключить привязки.
Матрица смежности выполняется на отдельном формате. Пример заполнения представлен на рис.5.
Проверьте, все ли распознанные тела-примитивы включены в матрицу смежности. Убедитесь, что между телами-примитивами полученными операцией “вычитание”, отсутствуют какие-либо взаимосвязи.
3.1. Построение 3D модели
Задача 3. Построить 3D модель геометрического тела.
3.1.1. Алгоритм построения.
Основой для построения 3D модели является использование 3D операций, расположенных на панели «Редактирование детали», таких как «Операция выдавливания», «Вращения» и т.д.
Построение выполняют, согласно матрице смежности, в порядке формообразования. Начинают с построения тела-примитива 1, затем 2 и т.д.
3.1.2. Строят внешние тела-примитивы.
3.1.3. Строят тела-примитивы, образующие полости.
3.2. Порядок построения 3D модели.
Порядок построения 3D модели представлен в Лабораторной работе №3 «Моделирование геометрического тела» часть 1, см. сайт www.dgec.mirea.ru. Пример выполнения Рис.12.

Рис.12