1. Первообразная и неопределенный интеграл.
2. Свойства неопределенного интеграла.
3. Таблица простейших интегралов.
4. Метод замены переменной в неопределенном интеграле.
5. Формула интегрирования по частям.
6. Интегрирование простейших рациональных дробей.
7.Метод неопределенных коэффициентов разложения правильной рациональной дроби на простейшие.
8.Интегрирование тригонометрических выражений: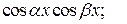 
Интегрирование выражений 
методом универсальной тригонометрической подстановки.
9. Интегрирование некоторых иррациональных выражений.
Литература: [ 1]; [2, гл. IX]; [4]; [5, гл. VII, §29-33]; [6, стр. 5-16].
Раздел II. Определенный интеграл
Тема 2. Определенный интеграл
1. Понятие определенного интеграла и его вычисление по формуле Ньютона-Лейбница.
2. Основные свойства определенного интеграла.
3. Замена переменной в определенном интеграле.
4. Интегрирование по частям в определенном интеграле.
5.Вычисление площади криволинейной трапеции и площади криволинейного сектора в полярной системе координат.
6. Вычисление длинны дуги кривой.
7. Вычисление объема тела вращения.
8. Физические приложения определенного интеграла.
9.Численное интегрирование: формулы прямоугольников, трапеций, Симпсона.
Литература: [1]; [2, гл. X]; [4]; [5, гл. VIII, §35-39]; [6, стр. 17-20].
Раздел III. Несобственные интегралы
Тема 3. Несобственные интегралы
1. Несобственные интегралы I рода (по бесконечному промежутку).
2. Несобственные интегралы II рода (от разрывных функций).
Литература: [1]; [2, гл. X, §2]; [4]; [5, гл. VIII, §40]; [6, стр. 21-22, стр. 41].
Вопросы программы для контрольной работы № 4
Раздел VI. Функции нескольких переменных
Тема 4. Функции нескольких переменных
1.Определение функции нескольких переменных. Примеры. Область определения, геометрическое представление области определения функции 2-х и 3-х переменных.
2. График функции 2-х переменных, линии уровня.
3. Поверхности уровня функции трех переменных.
4. Частные приращения и частные производные.
5. Частные производные высших порядков, смешанные производные.
6. Градиент функции в точке. Свойства вектора градиента.
7. Полное приращение и полный дифференциал функции в точке. Выражение полного дифференциала через градиент функции в точке.
8. Применение полного дифференциала для приближенного вычислениязначений функции.
9. Производная функциипо направлению и формула ее вычисления через градиент и направляющий вектор.
10. Касательная плоскость и нормаль к поверхности, заданной уравнением
F(x,y,z)=0 и уравнением z=f(x,y).
11. Формула Тейлора для функции двух переменных.
12. Максимум и минимум функции нескольких переменных. Необходимое условие экстремума.
13. Достаточное условие экстремума в стационарной точке для функции 2-х переменных.
14. Нахождение наибольших и наименьших значений функции, заданной в замкнутой области.
15. Метод наименьших квадратов обработки экспериментальных данных.
Литература: [1]; [2, гл.VIII]; [4]; [5, гл. IX].
Раздел V. Вектор – функция скалярного аргумента