1. Определение вектор-функции скалярного аргумента. Годограф.
2. Задание вектор-функции с помощью координат. Параметрическое задание линии (годографа).
3. Определение производной вектор-функции. Ее геометрический и механический смысл.
4. Дифференциал вектор-функции. Дифференциал длины годографа.
5. Дифференциал длины кривой, заданной параметрически.
6. Уравнения нормальной плоскости, проведенной через точку годографа.
7. Уравнения касательной, проведенной через точку годографа.
8. Вторая производная вектор-функции и ее механический смысл.
9. Средняя кривизна и кривизна линии в ее точке. Формула для нахождения кривизны годографа в заданной точке.
Литература: [2, гл. VII, §5, задачи 1127 – 1131, 1134, 1135, 1138, 1141 – 1143, 1145, 1146]; [1, гл. IX].
Раздел VI. Двойные интегралы
Тема 6. Двойные интегралы
1. Определение двойного интеграла, его геометрический смысл.
2. Свойства двойного интеграла.
3. Вычисление двойного интеграла в декартовой системе координат.
4. Вычисление двойного интеграла в полярной системе координат.
5. Вычисление объемов и площадей плоских фигур.
6. Механические приложения двойного интеграла: вычисление массы, статических моментов, моментов инерции, координат центра тяжести плоской пластины.
Литература: [1, т. 2, глава XIV]; [3, гл. XII, §1-6]; [4]; [5, гл. XI, §53]; [6, стр. 24-30].
Раздел VII. Криволинейные интегралы
Тема 7. Криволинейные интегралы
1. Определение и свойства криволинейного интеграла I рода (по дуге).
2. Формулы для вычисления криволинейного интеграла I рода.
3. Вычисление длины дуги.
4. Вычисление массы материальной дуги, ее моментов инерции, координат ее центра тяжести.
5. Определение и свойства криволинейного интеграла II рода (по координатам).
6. Формулы для вычисления криволинейного интеграла II рода.
7. Вычисление площади плоской фигуры.
8. Вычисление работы переменной вектор-силы.
Литература: [1, т. 2, глава XV]; [3, гл. XIII]; [4]; [5, гл. XII, §55, §56]; [6, стр. 31-33].
Определение варианта
Для определения номера своего варианта возьмите двузначное число, на которое оканчивается номер вашего шифра (номер вашей зачетной книжки). Если оно не превосходит 20, то это номер вашего варианта. В противном случае вычитайте из этого числа 20 до тех пор, пока остаток не станет меньше 21. Тогда этот остаток и есть номер вашего варианта.
Условие задачи состоит из общей для всех вариантов формулировки и двадцати вариантов конкретных данных. Именно для этих данных вам надлежит выполнить решение своего варианта. При оформлении контрольной работы условия задач следует переписывать полностью. Каждая контрольная работа выполняется в отдельной тетради с полями и сдается (отсылается) для проверки в установленное деканатом время (до начала сессии).
Контрольная работа № 3
Задача1. Найти неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием.
1. a)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
2. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
3. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
4. а)  б)
б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
5. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 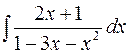 ; д)
; д)  ; е)
; е)  .
.
6. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
7. а)  ; б)
; б)  ; в)
; в) 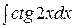 ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
8. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
9. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
10. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
11. а)  ; б)
; б) 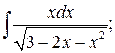 в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
12. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
13. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
14. а)  ; б)
; б)  в)
в) 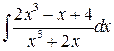 ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
15. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
16. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
17. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
18. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
19. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е) 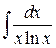 ;
;
20. а)  ; б)
; б)  в)
в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Задача 2. Вычислить определенные интегралы.
1.  . 2.
. 2.  . 3.
. 3.  .
.
4. 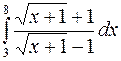 . 5.
. 5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  . 9.
. 9.  .
.
10.  . 11.
. 11. 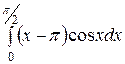 . 12.
. 12.  .
.
13.  . 14.
. 14.  . 15.
. 15.  .
.
16.  . 17.
. 17.  . 18.
. 18.  .
.
19.  . 20.
. 20.  .
.
Задача 3. Вычислить несобственные интегралы или доказать их расходимость.
1. 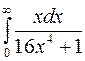 . 2.
. 2.  . 3.
. 3.  .
.
4.  . 5.
. 5. 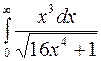 . 6.
. 6. 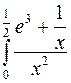
 .
.
7.  . 8.
. 8.  . 9.
. 9.  .
.
10. 
 . 11.
. 11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  15.
15. 
16.  . 17.
. 17.  . 18.
. 18. 
19.  . 20.
. 20. 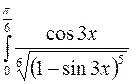 .
.
Задача 4. Используя определенный интеграл вычислить:
1. Площадь фигуры, ограниченной линиями:  .
.
2. Объем тела, полученного от вращения вокруг оси OX фигуры, ограниченной линиями 
3. Длину дуги линии 
4. Площадь фигуры, ограниченной линиями: 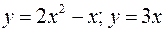 .
.
5. Объем тела, полученного от вращения вокруг оси OX фигуры, ограниченной линиями 
6. Длину дуги линии 
7. Площадь фигуры, ограниченной линиями: 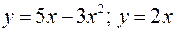 .
.
8. Объем тела, полученного от вращения вокруг оси OX фигуры, ограниченной линиями 
9. Длину дуги линии  .
.
10. Площадь фигуры, ограниченной линиями:  .
.
11. Объем тела, полученного от вращения вокруг оси OX трапеции, образованной прямыми  и осью OX.
и осью OX.
12. Длину дуги линии 
13. Площадь фигуры, ограниченной осью OX и линиями:  .
.
14. Площадь фигуры, ограниченной кривой  , прямыми
, прямыми  и осью OY.
и осью OY.
15. Объем тела, полученного от вращения вокруг оси OY фигуры, ограниченной линиями  .
.
16. Длину дуги линии  .
.
17. Площадь фигуры, ограниченной кривой:  .
.
18. Объем тела, полученного от вращения вокруг оси OX фигуры, ограниченной параболой  и прямой
и прямой  .
.
19. Длину дуги линии  .
.
20. Площадь фигуры, ограниченной кривой  , и прямыми
, и прямыми  .
.
Контрольная работа № 4
Задача 1. Дана функция трех переменных  и точка
и точка  требуется найти
требуется найти  производную по направлению
производную по направлению  в точке
в точке  . Написать уравнения касательной плоскости и нормали к поверхности уровня
. Написать уравнения касательной плоскости и нормали к поверхности уровня  в точке
в точке  .
.
1. 
2. 
3. 
4. 
5. 
6. 
7. 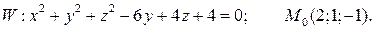
8. 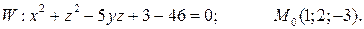
9. 
10. 
11. 
12. 
13. 
14. 
15. 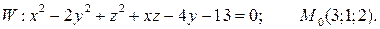
16. 
17. 
18. 
19. 
20. 
Задача 2. Вычислить приближенно, пользуясь дифференциалом, подходящей функции двух переменных:
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11  . 12.
. 12.  .
.
13.  . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19.  . 20.
. 20.  .
.
Задача 3. Найдите точки экстремума заданной функции.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 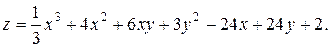
12. 
13. 
14. 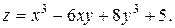
15. 
16. 
17. 
18. 
19. 
20. 
Задача 4. Дана вектор – функция  и точка
и точка  . В точке
. В точке  требуется найти:
требуется найти:
а)  и
и  ;
;
б) дифференциал длины годографа вектор-функции;
в) уравнение касательной к годографу в этой точке;