В круглом волноводе
Круглый волновод - односвязный закрытый волновод, поперечное сечение которого имеет форму круга радиуса r (см. рис. 2). Уравнение Гельмгольца в общем виде в цилиндрической системе координат имеет вид:
 , (12)
, (12)
где  - комплексная амплитуда электрического или магнитного поля.
- комплексная амплитуда электрического или магнитного поля.
Решение уравнения (12) ищется в виде комбинации функций Бесселя первого и второго рода (функций Неймана) порядка m (см. рис. 7) по радиальной координате (r) и тригонометрических функций по угловой координате (j).
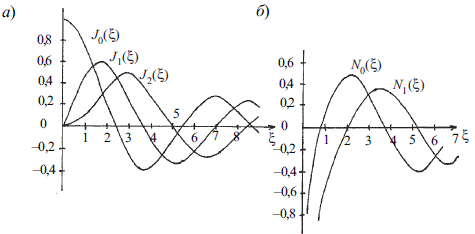
Рис. 7. Графики функций Бесселя Jm (а) и Неймана Nm (б)
В общем виде решение уравнения Гельмгольца в цилиндрической системе координат для продольной компоненты поля имеет вид:
 (13)
(13)
Однако в силу условий физической задачи поле в центре волновода не может быть бесконечно большим, что навязывается значением функции Неймана при r = 0, следовательно, необходимо положить Bm = 0 в (13). Кроме того, в (13) можем опустить sin(mj). Так как начало отсчета угла j может быть выбрано произвольно, выберем за начало отсчета полуплоскость j = const, в которой 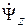 имеет максимальное значение. Косинус имеет максимальное значение при m j = 0, а синус при этом равен нулю. Перепишем (13) в соответствии с вышеизложенными соображениями:
имеет максимальное значение. Косинус имеет максимальное значение при m j = 0, а синус при этом равен нулю. Перепишем (13) в соответствии с вышеизложенными соображениями:
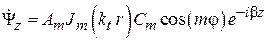 . (14)
. (14)
Запишем граничные условия для электромагнитного поля на стенке волновода, выполненного из идеального проводника:
 (15)
(15)
Решения уравнения (12) для электрических волн:
 (16)
(16)
Для магнитных волн:
 (17)
(17)
В отличие от прямоугольного волновода, в круглом волноводе поперечные волновые числа различны для электрических и для магнитных волн. Поперечные волновые числа для электрических волн находятся через корни функций Бесселя (n mn), а для магнитных – через корни производных функций Бесселя (c mn):
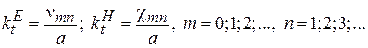
Значения первых корней функций Бесселя и их производных приведены в табл. 1 и 2.
Таблица 1. Корни функций Бесселя (n mn)
| Номер корня (n) | m = 0 | m = 1 | m = 2 |
| 2.405 | 3.832 | 5.135 | |
| 5.520 | 7.016 | 8.417 | |
| 8.654 | 10.173 | 11.620 |
Таблица 2. Корни производных функций Бесселя (c mn)
| Номер корня (n) | m = 0 | m = 1 | m = 2 |
| 3.832 | 1.840 | 3.054 | |
| 7.016 | 5.335 | 6.705 | |
| 10.174 | 8.536 | 9.965 |
Физический смысл индексов m и n, входящих в обозначение собственных мод круглого волновода. Индекс m входит в качестве постоянного коэффициента в аргументы функций cos(m j) и sin(m j), определяющих зависимость составляющих векторов Е и H собственных волн волновода от пространственной переменной j. Для выяснения общих закономерностей, определяющих зависимость этих составляющих от величины коэффициента m, достаточно рассмотреть одну из этих функций, например, cos(m j).
При m = 0 имеем cos(0 j)=1 и рассматриваемая составляющая не зависит от угла j (силовые линии соответствующего вектора представляют собой окружности).
При m = 1 зависимость от угла j определяется функцией cos j. В этом случае во всех точках диаметра j = ± (p/2) рассматриваемая составляющая будет равна нулю. Следовательно, во всех точках диаметра j = ± (p/2) будут находиться узлы (нулевые значения) этой составляющей. Поэтому данный диаметр называют «узловым». При m = 2 зависимость рассматриваемой составляющей от пространственной переменной j определяется функцией cos 2j и узловых диаметров будет два (j = ± (p/4), j = ± (3p/4)), при m = 3 – три и т.д.
Таким образом, индекс m определяет число узловых диаметров составляющих векторов E и H собственных волн круглого волновода и показывает какое количество узлов этих составляющих укладывается на половине окружности в поперечном сечении волновода.
Индекс n опосредованно входит в аргументы функций Бесселя и их первых производных, которые определяют зависимость составляющих векторов E и H собственных волн круглого волновода от пространственной переменной r. Величина n дает информацию о числе корней этих функций, приходящихся на диапазон изменения переменной r от 0 до a.
Следовательно, величина n определяет число узлов (нулевых значений) составляющих векторов E и H, укладывающихся вдоль радиуса волновода.
При n = 1 узлы рассматриваемой составляющей будут находиться непосредственно на стенке волновода, поэтому величина (n – 1) будет определять количество «узловых окружностей» составляющих векторов E и H собственных волн круглого волновода (окружностей, расположенных на плоскости поперечного сечения волновода, в каждой точке которых рассматриваемые составляющие равны нулю).
Рекомендации по графическому построению силовых линий векторов E и H в поперечном сечении круглого волновода. Знакомство с узловыми диаметрами и узловыми окружностями позволяет принять следующий порядок действий при построении картины силовых линий векторов E и H:
- в соответствии со значениями индексов m и n в поперечном сечении волновода наносятся контуры узловых диаметров и узловых окружностей;
- вдоль полученных «направляющих» наносятся силовые линии того вектора, который для данной собственной волны имеет только поперечные составляющие;
- перпендикулярно полученным силовым линиям «поперечного» вектора наносятся силовые линии другого вектора, не являющегося для данной собственной волны чисто поперечным;
- если силовые линии вектора E выходят из стенок волновода или входят в них, то на границе раздела они должны быть перпендикулярны этим стенкам;
- если силовые линии вектора H проходят вблизи стенок волновода, то на границе раздела они должны быть параллельны этим стенкам.
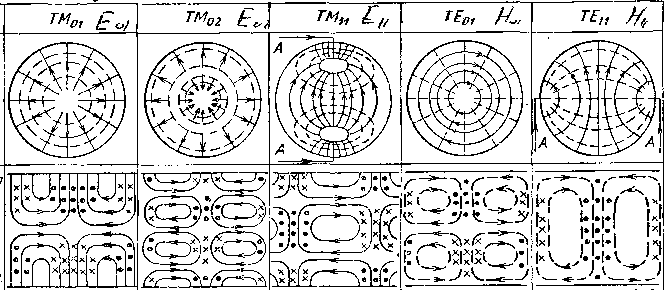
Рис. 6. Силовые линии векторов E и H для некоторых типов волн