
Решение задач
Изучение новой темы. Разбор задач
Давайте рассмотрим такую задачу: сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?
Решение: для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:
11, 14, 17, 41, 44, 47, 71, 74, 77.
Этот метод называется перебором вариантов. Таким образом, их трех данных цифр можно составить всего 9 различных двузначных чисел.
Эту задачу можно решить и другим способом. Его название – дерево возможных вариантов. Для этой задачи построена специальная схема.
Ставим звездочку. Она будет обозначать количество возможных вариантов.
Далее отводим от звездочки 3 отрезка. А почему? Как вы думаете? Так как в условии задачи даны 3 цифры – 1, 4, 7.
Ставим эти цифры на концах отрезков. Они будут обозначать число десятков в данном числе.
Далее от каждой цифры проводим по 3 отрезка. Почему? От цифры 1 три отрезка, от цифры 4 три отрезка и от цифры 7 также проводим три отрезка.
На концах этих отрезков записываем также цифры 1, 4, 7. Они будут обозначать число единиц.
рассмотрим, какие числа получились: 11, 14, 17, 41, 44, 47, 71, 74, 77. То есть всего получилось 9 чисел.
Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола.
Решение задач.
Итак, давайте решим несколько задач.
Сколько трехзначных чисел можно составить, используя цифры 3 и 5?
Ответ: всего 8 чисел.
В четверг в первом классе должно быть 3 урока: русский язык, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?
Ответ: всего можно составить 6 вариантов расписания.
Запишите все трехзначные числа, которые можно составить из цифр 0, 5, 9, используя при записи числа каждую цифру только один раз. Сколько всего таких чисел можно составить?
Ответ: всего 4 числа.
А теперь давайте сделаем так: мальчики решают задачу: Данила, Андрей и Коля собрались потренироваться в бросании мяча в баскетбольную корзину. У них только один мяч, и им надо договориться, кто за кем будет бросать мяч в корзину. Сколькими способами они могут занять очередь?
Девочки решают задачу: в костюмерной танцевального кружка имеются зелёные и жёлтые кофты, а также синие, красные и чёрные юбки. Сколько можно из них составить различных костюмов?
Домашнее задание
Откройте дневники и запишите домашнее задание. Решить задачи на карточках.
1. Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?
2. В палатке имеется 3 сорта мороженого: рожок, брикет и эскимо? Наташа и Данил решили купить по одной порции каждого сорта мороженого. Сколько существует вариантов такой покупки?
Итог урока
Урок 4. Правило суммы и правило произведения
Цели:
· познакомить учащихся с правилами произведения и суммы в комбинаторике;
· закрепить правила с помощью решения задач;
Оборудование:
Ход урока
1. Сообщение темы и целей
2. Домашнее задание на карточках
1) Сколькими способами можно выбрать гласную и согласную буквы из слова «ЗДАНИЕ»? (в слове «здание» 3 согласных и 3 гласных буквы. По правилу произведения получаем 3*3=9 способами)
2) Сколькими способами можно указать на шахматной доске два квадрата – белый и черный? Решите эту же задачу, если нет ограничений на цвет квадратов; если надо выбрать два белых квадрата. (На шахматной доске 64 клетки: 32 белых квадрата, 32 черных квадрата. По правилу произведения получаем число выбора двух квадратов: одного черного и одного белого: 32*32=1024.
Если нет ограничений на цвет, то первый квадрат можно выбрать 64 способами, а второй – 63 способами (один квадрат уже выбран), следовательно, 64*63=4032
Если надо выбрать два белых квадрата, то первый квадрат можно выбрать 32 способами, а второй квадрат – 31 способом, поэтому, 32*31=992.
3. Повторение
Решить задачу: сколько трехзначных чисел можно составить из цифр 0, 5, 8?
Ответ: 18 чисел
4. Работа по новой теме
Правило сложения: если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m+n способами.
Например: на тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5+4=9 способами.
Задача 1: сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?
Решение: составим дерево возможных вариантов.
Эту задачу можно решить по-другому и намного быстрее, не строя дерева возможных вариантов. Рассуждать будем так. Первую цифру трехзначного числа можно выбрать четырьмя способами. Так как после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4∙3∙2, т.е. 24.
Сформулируем правило умножения: если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить m∙п способами.
Например, решите задачу с помощью правила умножения: сколько пятизначных чисел можно составить из цифр 5, 9, 0, 6?
По правилу умножения получаем: 4∙4∙4∙4=256 чисел.
Правило умножения можно также проиллюстрировать.
Задача 2: из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
Решение: Пусть из города А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеется 2∙3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2∙3∙2=12 способов выбора туристами маршрута из города А к пристани.
Например: из пункта А в пункт В можно попасть десятью путями, а из пункта В в пункт С – девятью путями. Сколько имеется маршрутов из пункта А в пункт С через пункт В?
Решение: 10∙9=90 маршрутов
Задача 3: В кафе имеются три первых блюда, пять вторых блюд и два третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?
Решение: первое блюдо можно выбрать тремя способами, второе – пятью и третье – двумя, отсюда, по правилу умножения получаем 3∙5∙2=30 способами.
5. Первичное закрепление знаний
1. Сколько различных пятизначных чисел, делящихся на 10 можно составить из цифр 0, 1, 2, 3, 4? Каждую цифру можно использовать в записи только один раз.
2. Сколько пятизначных чисел, делящихся на три, можно составить из цифр 3, 4, 6, 7, 9 если каждое число не содержит одинаковых цифр?
3. Сколько шестизначных чисел можно составить из цифр 4, 5, 6, 7, 8, 9 так, чтобы каждое из них начиналось с комбинации «567»?
4. Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 так, чтобы каждое из них начиналось с комбинации «45»?
5. Сколько чётных положительных пятизначных чисел можно получить из цифр 5, 9, 6, 0, так, чтобы цифры в числе не повторялись?
6. Сколько чётных положительных пятизначных чисел можно получить из цифр 1, 2, 3, 4?
6. Итог урока
Урок 5. Самостоятельная работа по темам: «Поиск закономерностей», «Дерево возможных вариантов», «Правило произведения»
Цели:
· проверить знания по темам: «Поиск закономерностей», «Перебор возможных вариантов. Дерево возможных вариантов», «Правило суммы и правило произведения».
Оборудование: карточки с самостоятельной работой
Ход урока
1. Сообщение темы и целей
2. Самостоятельная работа
Самостоятельная работа
1. Сколько чисел, меньших ста, можно составить из цифр 0, 1, 2?
2. У рояля 88 клавиш. Сколькими способами можно извлечь последовательно 4 звука?
3. Сколько различных танцевальных пар (юноша, девушка) можно составить из пяти юношей и восьми девушек?
4. Сколько трехзначных чисел можно составить из трех различных, не равных двух цифр? Запишите их. Какова разность между самым большим и самым маленьким числом? Постройте дерево возможных вариантов.
| (23) | ||
| (__) |
5. Выявите закономерность и запишите число:
6. На тарелке лежат 10 яблок и 6 апельсинов. Сколькими способами можно выбрать один плод?
7. Из города А в город В ведут три дороги, а из В в С – две дороги. Сколькими способами можно пройти из А в С через В? Покажите чертеж.
8. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если: а) цифры не повторяются? б) цифры могут повторяться?
Ответы и решения
1. 0, 1, 2, 10, 11, 12, 20, 21, 22. Всего 9 чисел
2. 88∙88∙88∙88=59 969 536 способами
3. 5∙8=40 пар
4. 3∙3∙3=27
Самое большое число: 777
Самое маленькое число: 333
777 – 333 = 444 – разность
5. 24
6. 10+6=16 способами
7. 3∙2=6 способами
8. а) 60 чисел
б) 243 числа
3. Итог урока
Урок 6. Размещения
Цели:
· сформулировать определение размещений с повторениями, размещений без повторений
· закрепить на решении задач число размещений с повторениями, без повторений;
· рассмотреть понятие «кортеж», «факториал».
Оборудование: аншлаги с формулами
Ход урока
1. Сообщение темы и целей
2. Домашнее задание на карточках
1) Сколько букв русского алфавита можно закодировать, используя лишь комбинации точек и тире, содержащие только три знака? (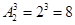 )
)
2) Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать? (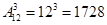 )
)
3) В классе 30 человек. Сколькими способами могут быть выбраны из них староста и казначей?
4) В чемпионате по футболу участвуют десять команд. Сколько существует различных возможностей занять командам первые три места?
3. Повторение
Решить задачу: сколькими способами можно обозначить вершины треугольника, используя буквы А,В,С,D,E и F?(60)
4. Работа по теме.
- Вспомните, что такое кортеж? Кортеж – это множество, в котором порядок элементов строго определен.
- Мы также часто можем встретить задачи, в которых нужно сосчитать число размещений с повторениями
4.1. Понятие «размещений с повторениями»
Множества, из элементов которых составляются кортежи, могут иметь общие элементы. В частности, все они могут совпадать с одним и тем же множеством, состоящим из п -элементов.
Кортежи длины k, составленные из элементов п -множества, называют размещениями с повторениями из п элементов по k.
Число размещений с повторениями находится по формуле: 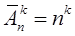
Вычислите: 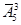 ;
; 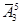
Решение: 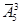 = 53=125;
= 53=125; 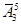 =35=243.
=35=243.
Понятие «факториал»
Произведение всех чисел от 1 до n называется факториалом и обозначается n!. В комбинаторике 0!=1 и 1!=!
Задача. Вычислите: 4!; 6!.
4!=4*3*2*1=24
6!=6*5*4*3*2*1=720
- Запишем в тетрадь таблицу
| n | ||||||||||
| n! | 5 040 | 40 320 | 362 880 | 3 628 800 | 39 916 800 |
Правило суммы и произведения – это общие правила решения комбинаторных задач. Кроме них в комбинаторике пользуются формулами для подсчета числа отдельных видов комбинаций, которые встречаются наиболее часто.
Понятие «размещений без повторений»
Нередко встречаются задачи, в которых требуется подсчитать число размещений без повторений
Кортежи длины k, составленные из элементов п -множества, так что все элементы каждого кортежа должны быть различными, называют размещениями без повторений из п элементов по k, а их число обозначают 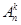 .
.
При этом размещения отличаются друг от друга как самими элементами, так и их порядком.
Число размещений без повторений находится по формуле: 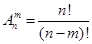
– Итак, в примере 1 нам нужно было составить двузначные числа из известных 3 цифр. По формуле получаем 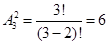 способов
способов
Задача. Сколько трехзначных чисел можно записать, используя цифры 1,3,6,7,9, если каждая их них может быть использована в записи только один раз? Постройте дерево возможных вариантов.
Решение: по формуле получаем: 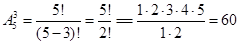 способов
способов
– Как вы думаете, как удобнее решать эти задачи: деревом возможных вариантов или по формуле?
5.Закрепление
Задача 1. Для запирания автоматической камеры применяется секретный замок, который открывается лишь тогда, когда набрано «тайное слово». Это слово набирают с помощью пяти дисков, на каждом из которых изображено 12 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова и подбирающего его наудачу?
Решение.Из условия задачи видно, что порядок выбираемых букв очень важен. Поэтому мы имеем дело с кортежем длиной 5 (пять дисков). Каждый элемент кортежа может быть выбран 12-ю способами (букв на каждом диске 12). Поэтому число комбинаций 125=248 831.
Задача 2. Сколько различных четырехзначных чисел можно составить из цифр 2, 6, 7, 8 и 9, если каждая цифра может входить в комбинацию несколько раз?
Решение. Порядок цифр важен, т.к. 2678 или 6278 – это разные числа. Поэтому имеем дело с кортежем длины 4 (четырехзначное число), каждый элемент которого можно выбрать пятью способами (цифр дано пять). Следовательно, число различных комбинаций равно 45=1024.
Задача 3. На референдуме предложены четыре вопроса, на которые надо ответить «да» или «нет». Сколько есть возможностей заполнения бюллетеня (на все вопросы надо дать ответ)?
Решение. Получаем кортеж длины 4 (столько вопросов в бюллетене), каждый элемент может быть выбран двумя способами («да» или «нет»). Поэтому число различных возможностей равно 24=16
Задача 4. Неудовлетворенные решением Париса Гера, Афина и Афродита обратились к трем мудрецам с просьбой назвать прекраснейшую из них. Каждый из мудрецов высказал свое мнение. Сколько могло возникнуть вариантов ответа на поставленный вопрос у этой тройки? (63=216)
Задача 5. У Лены есть восемь красок. Она хочет написать ими слова «Новый Год». Сколькими способами она может это сделать, если собирается каждую букву раскрашивать одним цветом? (88=16777216)
Задача 6. Сколькими различными способами можно распределить между шестью лицами две различные путевки в санаторий?
Решение. 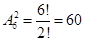
Задача 7. Из 20 учащихся надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?
Решение: 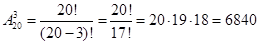 способами
способами
Задача 8. В классе изучаются 7 предметов. В среду 4 урока, причем все разные. Сколькими способами можно составить расписание на среду?
Решение: 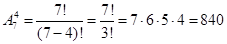 способов
способов
Задача 9. В чемпионате по футболу участвуют десять команд. Сколько существует различных возможностей занять командам первые три места?
Решение: 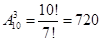
Задача 10. Из десяти различных книг выбирают четыре для посылки. Сколькими способами это можно сделать?
Решение. 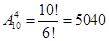
Задача 11. Для запирания сейфа на диск нанесены 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова? (125=248 832 удачных попыток, следовательно, неудачных 248 831)
Итог урока
Что нового узнали на уроке?
По какой формуле находится число размещений без повторений, с повторениями?