Цели:
· Проверить знания по темам: «Размещение без повторений», «Размещение с повторениями» с помощью теста.
Оборудование: карточки с тестом
Ход урока
1. Сообщение темы и целей
2. Тест
1. Из 30 студентов класса надо выбрать хозяйку класса, старосту и физорга. Сколькими способами это можно сделать?
А) 24360 б) 2730 в) 6720
2. В конкурсе песен «Галерея звезд» участвуют 15 человек. Сколькими способами могут распределиться между ними места?
А) 24360 б) 2730 в) 6720
3. Сколько трехзначных чисел можно составить из цифр 5, 6, 8, 7, 1?
А) 243 б) 2730 в) 6720
4. Для запирания сейфа на диск нанесены 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова?
А) 248 832 б) 248 831 в) 248 833
5. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6?
А) 24360 б) 4 096 в) 6720
6. Пять разных предметов раздают 8 людям, причем может случиться так, что некоторые получат по несколько предметов. Сколькими способами может быть произведен раздел?
А) 24360 б) 2730 в) 6720
7. Сколькими способами из колоды, содержащей 36 карт, можно выбрать по одной карте каждой масти?
А) 24360 б) 2730 в) 1 413 720
8. Сколько можно составить трехзначных чисел из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9? Рассмотрите два случая: а) цифры, входящие в одно и тоже число различны; б) среди входящих в одно и тоже число, могут быть одинаковые.
А. а)60 480 б)19 683 в) 672
Б. а)19 683 б) 60 480 в) 6720
Ответы и решения
1. 
способами
2. 
способами
3. 
чисел
4. 125=248 832 – удачных попыток, тогда неудачных 248 831.
5. 46=4 096 чисел
6. 
спсобами
7. 
способами
8. а) 
чисел
9. б) 39=19 683 чисел
3. Итог урока
Урок 8: Перестановки
Цели:
· познакомить учащихся с перестановками без повторений, перестановками с повторениями;
|
|
· закрепить новые формулы с помощью решения задач.
Оборудование: аншлаги с формулами
Ход урока
1. Сообщение темы и целей
2. Домашнее задание:
1) Сколькими способами можно разместить 12 человек за столом, на который поставлено 12 приборов?
2) Сколькими способами можно установить дежурство по одному человеку в день среди семи учащихся группы в течение семи дней?
3) Сколько различных слов можно получить, переставляя буквы слова «ингредиент»?
4) Сколькими способами можно посадить за круглый стол пять мужчин и пять женщин так, чтобы никакие два лица одного пола не сидели рядом?
4. Работа по теме
4.1. Повторение
Решите задачу: на железнодорожной станции имеется n семафоров. Сколько может быть дано различных сигналов при помощи этих семафоров, если каждый семафор имеет три состояния: горит либо зеленый, либо желтый, либо зеленый цвет.
Решение: имеем кортеж длины n (дано n семафоров), каждый элемент которого можно выбрать тремя способами (каждый семафор имеет три состояния). Поэтому различных сигналов можно дать 3n.
- Дайте определение размещений без повторений
- Что такое факториал?
4.2. Понятие «перестановки без повторений»
Два размещения без повторений из n элементов по n, состоящие из одних и тех же элементов, расположенных в различном порядке называются перестановками без повторений из n элементов. Их число обозначают Рn.
- Выведем формулу.
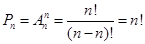
Следовательно, число перестановок без повторений находится по формуле: Рп=n!
Вычислите: Р3; Р5
Р3=3!=6; Р5=5!=120
4.3. Понятие «перестановки с повторениями»
Пусть дан кортеж длинны п, составленный из элементов множества Х= { х1, …, хk }. Причем буква х1 входит в этот кортеж п1 раз, буква хk = пk раз. Тогда п=п1 + … +пk. Если переставлять в этом кортеже буквы, то будут получаться новые кортежи, имеющие тот же состав. Эти кортежи называются перестановками с повторениями из букв х1,…, хk, имеющими состав (п1, …, пk).
|
|
Число таких перестановок обозначается Р(п1, …, пk) и находится по формуле:
Упражнение. Вычислите: Р (2, 5, 3); Р (1, 2, 3, 4).
Решение. Р (2, 5, 3); п =2+5+3=10, п1 =2, п2 =5, п3 =3
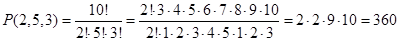
5. Закрепление
Задача 1. Найдите число способов расстановки 8 ладьей на шахматной доске, при которых они не бьют друг друга.
Решение. Каждый искомый способ задается перестановкой 8 чисел1,2, … 8. Эти числа указывают номера горизонталей занятых полей на первой, второй, …, восьмых вертикалей. Значит, таких перестановок 8!. Таким образом, ладьи можно расставить 8!=40 320 способами.
Задача 2. Сколькими способами можно представлять друг с другом цифры 1, 2, 3, 4?
Решение. Р4=4!=24.
Задача 3. За столом пять мест. Сколькими способами можно расставить пятерых гостей?
Решение. Р5=5!=120
Задача 4. У Лены есть 8 разных красок. Она хочет написать ими слова «Новый Год». Сколькими способами она может это сделать, если каждая буква может быть раскрашена одним цветом и все 8 букв должны быть разные по цвету.
Решение. Присвоим каждой краске номер от 1 до 8. Тогда каждый искомый способ задается перестановкой 8 чисел 1,2, …, 8. Значит, таких перестановок 8!. Поэтому она может написать «Новый Год» 8!=40 320 способами.
Задача 5. Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
|
|
Решение. 5!=120
Задача 6. Сколько различных кортежей получится, если переставлять буквы слова «математика»?
Решение. Это слово имеет состав: м – 2, а – 3, т – 2, е – 1, и – 1, к – 1, то есть (2, 3, 2, 1, 1, 1), поэтому получим Р(2,3,2,1,1,1)= 
Задача 7. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней она дает сыну по 1 фрукту. Сколькими способами это может быть сделано.
Решение. Р(2,3)= 
Задача 8. Сколькими способами можно положить 28 различных открыток в 4 одинаковых конверта так, чтобы в каждом конверте было по 7 открыток?
Решение. Пометим конверты цифрами 1,2,3,4, тогда число различных раскладок равно Р(7,7,7,7)= 
. Вычислять это значение не будем, так как оно очень большое.
Сотрем пометки. Теперь конверты можно произвольно переставлять друг с другом, не меняя результата расклада (теперь они не отличаются друг от друга). Так как число различных перестановок четырех конвертов равно Р4=4!, то число различных раскладов уменьшается в Р4=4! и поэтому оно равно 
.
Задача 9. Сколькими способами можно усадить за стол трех мальчиков и трех девочек так, чтобы никакие две девочки не сидели рядом?
Решение. 3!∙3!=36 способами
6. Итог урока
- Что такое перестановки без повторений?
- По какой формуле находится число перестановок без повторений?
Урок 9. Сочетания
Цели:
· познакомить учащихся с сочетаниями без повторений и с повторениями;
· закрепить новые формулы с помощью решения задач.
Оборудование: аншлаги с формулами
Ход урока
1. Сообщение темы и целей
2. Домашнее задание на карточках
1) Из 20 учащихся кружка математики четверых необходимо отправить на олимпиаду. Сколькими способами можно составить команду?
Решение: 
3) В вазе стоят 10 белых и 5 красных роз. Сколькими способами можно выбрать из вазы букет, состоящий из двух красных и одной белой розы?
Решение: 
· 
= 
= 100. 
3) Сколько существует различных треугольников, длины сторон которых принимают значения 5, 6, 7, 8, 9? Сколько из них равносторонних, равнобедренных и разносторонних?
4. Повторение
1) Назовите формулу размещений без повторений, размещений с повторениями, перестановок без повторений и перестановок с повторениями;
2) Назовите правила произведения и суммы.
5. Работа по новой теме
5.1. Понятие «сочетаний без повторений»
Задача: рассмотрим все возможные способы составления букетов, в которых по-разному сочетаются три розы из данных пяти роз разного цвета, например: белая, красная, черная, желтая и чайная.
Введем определение:
Сочетаниями без повторений из n элементов по т элементов называются соединения, каждое из которых состоит из m элементов, взятых из данных n элементов.
Число сочетаний из п элементов по m обозначают 
и читают «С из n по m ».
Два сочетания из п элементов по т отличаются друг от друга хотя бы одним элементом. В отличие от размещений, порядок следования элементов здесь не учитывается.
Число сочетаний без повторений равно: 
Понятие «сочетаний с повторениями»
- Число сочетаний с повторениями из n элементов по m выражается через число сочетаний без повторений.
- Назовите формулу числа сочетаний без повторений.
Найдем число сочетаний с повторениями из четырех элементов А, Б, В, Г по три элемента:
| ААА | АБВ | БББ | ГГГ |
| ААБ | АБГ | ББВ | ВВВ |
| ААВ | АВВ | ББГ | ВВГ |
| ААГ | АВГ | БВВ | ВГГ |
| АББ | АБГ | БВГ | ГГГ |
Число сочетаний с повторениями обозначается символом 
. В данном случае мы получили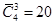 
, тогда как число сочетаний без повторений из четырех элементов по 3 есть 
.
Формула числа сочетаний из m элементов по n элементов с повторениями имеет вид:
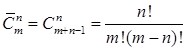
Решим предыдущую задачу с помощью этой формулы.
Сочетание с повторениями из m элементов по n элементов может содержать любой элемент сколько угодно раз от 1 до n включительно, либо совсем не содержать его. Во всех случаях два соединения не считаются различными сочетаниями, если они отличаются друг от друга только порядком расположения элементов.
6. Первичное закрепление
Давайте сначала выясним, чем отличаются размещения от сочетаний? В сочетаниях порядок элементов не важен, а размещениях – важен!
Задача 1. Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Решение: каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3. Следовательно, по формуле получаем 
Задача 2. В магазине «Филателия» продается 8 различных марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение: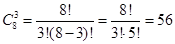 
Задача 3. На полке стоит 12 книг: англо-русский словарь и 11 художественных произведений на английском языке. Сколькими способами читатель может выбрать 3 книги, если:
а) словарь нужен ему обязательно;
б) словарь ему не нужен?
Решение:
а) 
б) 
Задача 4. В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков и трех девочек. Сколькими способами это можно сделать?
Решение: 
Задача 5. На тренировках занимаются 10 баскетболистов. Сколько различных стартовых пятерок может образовать тренер?
Решение. 
Задача 6. Сколько наборов из семи пирожных можно составить, если в продаже имеется четыре сорта пирожных?
Решение. 
наборов
Задача 7. Сколько существует различных треугольников, длины сторон которых принимают значения: 8, 10, 12 и 14 см? Сколько среди них равносторонних, равнобедренных, разносторонних?
Решение: число различных треугольников равно числу сочетаний с повторениями из четырех элементов по три: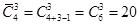 
.
Из них количество разносторонних треугольников равно числу сочетаний без повторений их четырех элементов по три, т.е. 
. Количество равносторонних треугольников – 4, а равнобедренных треугольников: 20 – 4 – 4=12.
Задача 8. Сколько всего существует результатов опыта, заключающегося в подбрасывании двух одинаковых игральных костей?
Решение. 
Задача 9. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? 8 открыток? 8 различных открыток?
Решение. 
293 930 способами.
6. Итог урока
- Что нового вы сегодня узнали на уроке?
- Чем отличаются сочетания от размещений? (сочетания – порядок не важен, размещения – порядок важен!)