Так как электродные процессы представляют собой аналог химических реакций, отличающиеся тем, что включают одну или несколько стадий переноса заряда, то для них справедливы общие закономерности химической кинетики. Рассмотрим обратимую электродную реакцию растворения (восстановления ионов) металла типа
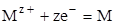 (1.86)
(1.86)
Реакция переноса для процесса такого типа состоит из следующих последовательных стадий:
1 - разложение исходного комплекса, в котором находится ион металла в растворе на свободный ион и свободный комплексообразователь;
2 - дегидратация иона металла
3 - рекомбинация дегидратированного иона металла и электронов, выходящих из металлического электрода.
Согласно кинетическим закономерностям, парциальная анодная плотность тока ja реакции (1.86) равна
 (1.87)
(1.87)
а для катодной плотности тока имеем
 (1.88)
(1.88)
где 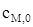 и
и  - соответственно поверхностные концентрации металла М и ионов металла Mz+ на межфазной границе металл - электролит, Ea и Ek - соответственно энергии активации ионизации металла и разряда ионов металла;
- соответственно поверхностные концентрации металла М и ионов металла Mz+ на межфазной границе металл - электролит, Ea и Ek - соответственно энергии активации ионизации металла и разряда ионов металла; 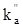 и
и  - константы, соответствующие предэкспоненциальному множителю, введенному в теории абсолютных скоростей реакции.
- константы, соответствующие предэкспоненциальному множителю, введенному в теории абсолютных скоростей реакции.
В теории абсолютных скоростей реакции предполагается, что энергия активации процесса зависит от энергетических параметров переходного (активированного) состояния реагентов, которое предшествует химическому превращению. Определение этих параметров в настоящее время невозможно. Эта проблема решается введением коэффициента переноса a, который учитывает изменение энергии активации, обусловленное разностью потенциалов (Dj) между металлом и раствором (гальвани-потенциалом). Изменение энергии активации с изменением электродного потенциала имеет вид, представленный на рис.1.8.

Рис. 1.8. Зависимость энергии активации от величины электродного потенциала
Согласно энергетической диаграмме анодную и катодную энергии активации можно представить в виде
 (1.89)
(1.89)
 (1.90)
(1.90)
Учитывая, что на практике используют величины электродных потенциалов, измеренных относительно электродов сравнения, можно получить соотношения между анодной и катодной составляющими плотности тока и измеренным электродным потенциалом:
 (1.91)
(1.91)
 (1.92)
(1.92)
где
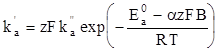 (1.93)
(1.93)
 (1.94)
(1.94)
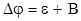 (1.95)
(1.95)
B - константа, учитывающая разницу между электродным и гальвани-потенциалом и зависящая от выбора электрода сравнения.
В результате можем записать уравнение для суммарного тока электродного процесса в виде
 (1.96)
(1.96)
Согласно уравнению (1.82), при равновесном потенциале получаем
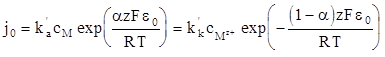 (1.97)
(1.97)
Принимая во внимание уравнение (1.84), можно получить зависимость тока электродной реакции от перенапряжения, описывающую поляризационную кривую
 (1.98)
(1.98)
или, учитывая (1.97),
 (1.99)
(1.99)
На рис.1.9 приведены поляризационные кривые для двух электродных процессов с разными токами обмена.

Рис 1.9 Поляризационные кривые для двух электродных процессов с разными токами обмена.
Рассмотрим некоторые свойства поляризационной кривой. При больших анодных перенапряжениях, когда h>>RT/zF, ток jk пренебрежимо мал, вторым членом в уравнении (1.99) можно пренебречь. Тогда суммарная плотность тока определяется только анодной плотностью тока:
 (1.100)
(1.100)
Если теперь преобразовать уравнение (1.100) в зависимость перенапряжения от плотности тока, то получим
 (1.101)
(1.101)
Уравнение (1.101) хорошо согласуется с эмпирически установленным соотношением
 (1.102),
(1.102),
полученным Тафелем при изучении реакции выделения водорода. Линейные зависимости h-lg(j) называют тафелевскими прямыми, а тангенс угла наклона этих зависимостей – тафелевским наклоном. Тафелевский наклон определяется выражением
 (1.103)
(1.103)
или, как следует из уравнений (1.101) - (1.102):
 ,
,  (1.104).
(1.104).
Очевидным следствием уравнения (1.104) при a=0,5 является равенство
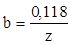 (1.105)
(1.105)
Таким образом, для одностадийного процесса переноса заряда тафелевский наклон определяется валентностью реакции.
В случае низких перенапряжений (h<<RT/zF) ни одним членом уравнения (1.99) пренебречь нельзя. Однако в силу малости экспоненциальных членов можно применить разложение экспоненты в ряд и ограничиться первыми членами разложения. При этом суммарную плотность тока можно выразить в виде:
 (1.106)
(1.106)
Уравнение (1.106) показывает, что вблизи равновесного потенциала плотность тока почти линейно меняется с изменением перенапряжения, а наклон линейного участка зависит от величины тока обмена. Зависимость (1.106) по своему характеру подобна закону Ома, в котором роль сопротивления играет величина
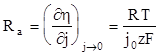 (1.107)
(1.107)
Поэтому плотность тока обмена можно определить, измеряя сопротивление переноса заряда Ra.
Все проведенные рассуждения справедливы лишь, если реакция переноса протекает в одну стадию. В случае, когда в суммарной реакции переносится более одного заряда, этот перенос может быть результатом нескольких последовательных стадий переноса. Тогда требуется рассмотрение системы уравнений, описывающих скорость каждой реакции, а уравнение суммарной поляризационной кривой принимает более сложный вид, чем предсказываемый уравнением (1.99).