Диффузионная поляризация

 

Рассматривая особенности реакции переноса заряда, мы предполагали, что концентрация реагирующих ионов у поверхности электрода постоянна за счет достаточно быстрой доставки реагентов и отвода продуктов взаимодействия. Очевидно, что такое положение возможно лишь при невысокой скорости реакции переноса, т.е. при малых плотностях тока. При высокой плотности тока концентрация участвующих в реакции частиц становится отличной от их концентрации в объеме раствора. В этих условиях между поверхностью электрода и раствором активируется массоперенос, в котором основную роль играет диффузия. Электромиграция ионов и конвективное перемешивание также влияют на кинетику массопереноса, но диффузия представляет собой наиболее заторможенный процесс. Поэтому именно диффузия заметно влияет на кинетику суммарного электродного процесса в целом.

Для более наглядного представления о влиянии массопереноса предположим, что другие стадии процесса в рассматриваемых условиях не лимитируют скорость электродной реакции. Такое допущение означает, что ток обмена рассматриваемой электродной реакции достаточно велик, чтобы обеспечить незначительное отклонение от равновесного потенциала, соответствующего концентрации потенциалопределяющих ионов (c_i,0) вблизи поверхности электрода. Поэтому неполяризуемый электрод находится почти в равновесии со слоем раствора, непосредственно контактирующим с электродом.

В соответствии с уравнением для равновесного потенциала (1.71) реакции типа (1.65) имеем

(1.108)

Вследствие диффузионных затруднений концентрация частиц вблизи поверхности электрода c_i,0 отличается от соответствующей величины в объеме раствора c_i. Поэтому и электродный потенциал e отличается от равновесного потенциала e₀, соответствующего объемной концентрации c_i. Следовательно, для диффузионного перенапряжения можно записать

(1.109)

Для простых ионно-металлических электродов, на которых протекает реакция (1.85), электродный потенциал равен:

(1.110)

Следовательно, для диффузионного перенапряжения получаем

(1.111)

Для того чтобы установить взаимосвязь между током и перенапряжением, необходимо обратиться к законам диффузионного массопереноса. Согласно 1-му закону Фика поток i-го компонента (J_i) в условиях линейной диффузии будет равен

, (1.112)

где D_i - коэффициент диффузии i-х частиц, а (¶с_i/ ¶x)_x®0 - градиент концентрации вблизи поверхности электрода. Объединяя законы Фика и Фарадея, получим

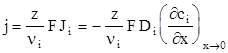(1.113)

где n_i - стехиометрическое число i-го компонента. Отношение z/n_i считают положительным, если частицы i расходуются в катодной реакции и образуются в ходе анодной.

В стационарном состоянии по второму закону Фика следует, что

(1.114)

Значит, градиент концентрации во всем диффузионном слое является постоянным. Если поверхностная концентрация реагирующих частиц равна c_i,0, а в объеме раствора - c_i, то градиент концентрации частиц в диффузионном слое равен

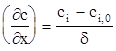(1.115)

где d - толщина диффузионного слоя. Поэтому плотность диффузионного тока можно представить в виде

(1.116)

Очевидно, что максимальное значение плотности диффузионного тока достигается, когда c_i,0 становится равной 0. Это значение плотности тока называется предельной плотностью диффузионного тока и определяется выражением

(1.117)

Используя уравнения (1.116) и (1.117), можно записать

(1.118)

 

Рис. 1.10. Зависимость плотности тока от перенапряжения при диффузионной поляризации

 

Подставив (1.118) в (1.111), получим

(1.119)

или

(1.120)

Зависимость плотности тока от перенапряжения при диффузионной поляризации приведена на рис. 1.10. Из уравнений (1.119), (1.120) и рис. 1.10 видно, что предельный ток наблюдается при катодном осаждении металла, а при анодном растворении появления предельного тока ожидать нельзя.

Как следует из уравнения (1.117), величина предельного диффузионного тока при прочих равных условиях обратно пропорциональна толщине диффузионного слоя. Известно, что толщина диффузионного слоя пропорциональна концентрации частиц в степени -1/4 и коэффициенту диффузии в степени 1/4. Подставляя эту зависимость с поправочным коэффициентом A в (1.117), получим, что предельная плотность диффузионного тока зависит от концентрации электролита как

(1.121)

Далее будет показано, что эта зависимость выполняется при определении условий формирования слоев наноструктурированного кремния.

 

1.9 Полупроводниковые электроды в электрохимических процессах

 

Ранее мы подробно рассмотрели электродные процессы, протекающие на металлических электродах. Однако на практике часто приходится иметь дело с поверхностью металла, покрытой оксидной пленкой. Свойства многих оксидов металлов носят полупроводниковый характер. Поэтому учета влияния полупроводниковой природы поверхности электрода позволяет объяснить некоторые особенности равновесия и кинетики электродных реакций. Более того, электрохимическая обработка находит широкое применение в технологии полупроводниковых материалов для целей твердотельной электроники.

Полупроводниками принято называть вещества, проводимость которых лежит в интервале примерно 10^-10-10⁴ (Ом^.см)^-1. Полупроводники имеют запрещенную зону, которая определяет специфику их электрохимических свойств. В отличие от металлов, где перенос электричества осуществляется только электронами, электропроводность полупроводников обусловлена электронами и дырками.

Если полупроводник приведен в контакт с раствором электролита, то на поверхности раздела возможно протекание электродной реакции, обусловленное разностью электрохимических потенциалов частиц в растворе и полупроводнике. Перенос электронов будет продолжаться до тех пор, пока электрохимические потенциалы электронов в растворе и полупроводнике не станут равны друг другу. В результате перераспределения зарядов в обеих фазах вблизи поверхности раздела сформируются области пространственного заряда, образующие в совокупности двойной электрический слой. Объемный заряд в полупроводнике может образоваться также в результате адсорбции на его поверхности заряженных ионов. Природа пространственного заряда в полупроводнике обусловлена перераспределением электронов и дырок вблизи поверхности.

Согласно общепринятой модели, в пределах двойного электрического слоя выделяют три области: область пространственного заряда в растворе (слой Гуи-Чэпмена), переходную область или слой Гельмгольца и область пространственного заряда в полупроводнике.

На рис.1.11 схематически представлено пространственное распределение заряда и Гальвани-потенциала j(el/sc) на межфазной границе полупроводник/электролит. Следует специально отметить, что развитый слой Гуи-Чэпмена формируется лишь в растворах электролитов относительно невысокой концентрации (£10^-1 моль/л).

В соответствие с обозначениями, принятыми на рис.1.11, полный скачок потенциала на межфазной границе электролит-полупроводник j_e/s определяется суммой скачков потенциала в каждой из частей области пространственного заряда:

(1.122)

Рис 1.11 Пространственное распределение заряда и Гальвани-потенциала j(el/sc) на межфазной границе полупроводник/электролит.

 

Следует обратить внимание на важное в методическом плане обстоятельство, что в электрохимии за положительное направление электродного потенциала принято направление, которое соответствует росту положительного заряда электрода, а нулевое значение принимается потенциал электрода сравнения. Причем это значение с точностью до константы равно потенциалу в объеме раствора. С другой стороны, в физике полупроводников потенциалы отсчитывают от значения в глубине полупроводника, и положительному потенциалу соответствует отрицательный пространственный заряд. Поэтому потенциал поверхности полупроводника оказывается противоположным по знаку третьему слагаемому в квадратных скобках в уравнении (1.122), т.е.

(1.123)

В зависимости от свойств перечисленных слоев, под действием электрического поля распределение потенциалов в них будет различным. При поляризации электрода в общем случае меняются все составляющие Гальвани-потенциала, что может быть выражено уравнением

(1.124)

Для определения распределения потенциала в полупроводнике воспользуемся самосогласованным уравнением Пуассона-Больцмана

(1.125)

Граничными условиями для уравнения (1.125) служат соотношения

, , (1.126)

которые вытекают из условия электронейтральности в объеме полупроводника. Кроме того, j(¥)=0 в соответствии с выбором нуля потенциала.

При невысоких потенциалах, когда

, (1.127)

разлагая экспоненты в ряд и учитывая условие электронейтральности, уравнение (1.125) можно преобразовать к виду

(1.128)

Аналитическое решение уравнения (1.128) имеет вид

(1.129)

где

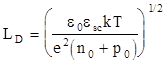(1.130)

Характеристическая длина L_D, называемая дебаевской длиной или длиной экранирования, определяет масштаб изменения физических величин в области пространственного заряда в полупроводнике.

В случае сильнолегированного полупроводника n-типа при отрицательном смещении на поверхности образуется область, обедненная электронами, которую называют областью пространственного заряда (ОПЗ). Распределение потенциала в ОПЗ описывается уравнением

(1.131)

где

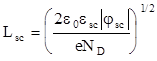(1.132)

В общем случае напряженность электрического поля в полупроводнике имеет вид

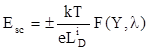(1.133)

Здесь - дебаевская длина для собственного полупроводника, определяемая выражением

(1.134)

Функция F(Y, l) определяется выражением

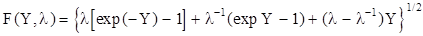, (1.135)

где

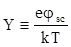, (1.136)

Значения функции F(Y, l) табулированы, что позволяет достаточно просто определить значение напряженности электрического поля в области пространственного заряда в полупроводнике.

Необходимо помнить, что для вырожденных полупроводников полученные уравнения не выполняются. Вырождение наступает при очень высокой концентрации носителей, когда длина волны де Бройля носителя заряда становится соизмеримой со средним расстоянием между частицами. Такая ситуация возможна при высокой степени легирования или при больших электрических полях. В этом случае энергия носителей заряда вблизи поверхности оказывается квантованной. Значит, в запрещенной зоне появляются дискретные разрешенные уровни, которые оказывают влияние не только на электрофизические свойства самого полупроводника, но и могут изменять кинетические параметры электрохимических процессов на поверхности полупроводникового электрода.

Так как вырождение имеет место при достаточно высокой концентрации носителей вблизи поверхности, то оно сопровождается своеобразной “металлизацией” приповерхностной области, изменяющей оптические и электрохимические свойства полупроводникового электрода. Поэтому при поляризации электрода в условиях поверхностного вырождения прикладываемая разность потенциалов оказывается сосредоточенной в слое Гельмгольца, как это имеет место на металлических электродах.

Распределение потенциала в растворе вблизи поверхности электрода, в ионном диффузионном слое для одно-однозарядного электролита определяется уравнением

(1.137)

где с(-¥) - объемная концентрация одного из сортов ионов в глубине раствора, e_el - статическая диэлектрическая проницаемость раствора.

Граничными условиями к уравнению (1.137) являются соотношения

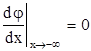и (1.138)

где j‘ - значение потенциала на внешней плоскости Гельмгольца, отсчитанное от потенциала в глубине раствора. Точное решение уравнения (1.137) имеет вид

(1.139)

где L_G - характеристическая длина, определяющая размер области пространственного заряда в растворе. Длина L_G, введенная Гуи, определяется свойствами раствора и имеет следующее аналитическое выражение

(1.140)

Электрическое поле на границе диффузионного слоя в электролите определяется уравнением

(1.141)

Используя соотношения (1.139) и (1.141), можно связать между собой величины потенциалов в полупроводнике и электролите. Учитывая условие равенства векторов электрической индукции на границе раздела фаз, можно записать

(1.142)

Так как напряженность электрического поля связана с потенциалом соотношением

(1.143),

то всегда можно определить величины потенциалов, зная условия распределения потенциала хотя бы в одной из фаз.

В связи с изложенным следует отметить ряд важных моментов. Все проведенные расчеты проводились в предположении о равновесии зарядов в областях пространственного заряда в полупроводнике и растворе. При протекании тока равновесие может быть искажено. Однако в некоторых случаях эти искажения минимизируются. Так, если величина протекающего тока значительно меньше предельного диффузионного тока реагирующих веществ в растворе, то нарушением равновесия в растворе можно пренебречь. Поэтому изучение кинетики электродных реакций проводят в условиях, когда диффузионные ограничения незначительны. В отношении полупроводника следует отметить, что в условиях образования обедненного слоя в полупроводнике основной заряд в ОПЗ создается неподвижными ионизированными атомами примеси. Поэтому даже при достаточно больших токах искажения потенциала оказываются незначительными.

Отметим несколько важных на практике следствий соотношения (1.142). Если концентрация электролита достаточно велика, то основное изменение потенциала происходит в полупроводнике и слое Гельмгольца и наоборот, если электролит обеднен заряженными частицами, а полупроводник сильно легирован.

Все сказанное остается справедливым в условиях поляризации электрода с помощью внешнего источника напряжения. Изменение электродного потенциала сопровождается при этом изменением всех составляющих Гальвани-потенциала.

Рассмотрим два предельных случая распределения потенциала в системе электролит – полупроводник при внешней поляризации.

1. Если изменения потенциалов в слое Гельмгольца и ионном диффузионном слое значительно меньше изменения потенциала в полупроводнике, то положения всех энергетических уровней поверхности и, в частности границы энергетических зон полупроводника остаются неизменными по отношению к энергетическим уровням в электролите и к электроду сравнения. В этом случае говорят, что границы зон “закреплены на поверхности”.

2. Если основное изменение потенциала сосредоточено в слое Гельмгольца, то уровни энергии на поверхности сдвигаются относительно уровней энергии в растворе на величину, равную Dj_H. По отношению к уровню Ферми в полупроводнике края зон сохраняют то же положение, что и до приложения потенциала, так как j_sc остается постоянным. В отличие от предыдущего, в этом случае говорят, что границы зон “открепляются”. Иногда такое явление называют “закреплением” уровня Ферми.

В реальных системах часто наблюдается промежуточный случай, когда при поляризации электрода изменяются оба скачка потенциала j_sc и j_H, так что ни границы зон, ни уровень Ферми не оказываются закрепленными.

На свойства границы раздела полупроводник - электролит оказывают существенное влияние поверхностные состояния. Реальная поверхность полупроводника содержит различные типы поверхностных состояний и соответствующих им электронных уровней. Эти уровни могут быть как донорными или акцепторными, так и амфотерными. Их концентрация и тип зависит от обработки поверхности и может достигать 10¹⁴-10¹⁵ см^-2. Наличие большого числа заряженных поверхностных состояний может привести к перераспределению падения потенциала между полупроводником и раствором. Влияние заряда поверхностных состояний Q_ss на E_sc и E_H дается соотношением

(1.144)

Для оценки влияния поверхностных электронных уровней на распределение скачка потенциала и заряда двойного электрического слоя удобно воспользоваться простейшей моноэнергетической моделью. Если все электронные поверхностные уровни характеризуются одинаковой энергией E_ss и могут отдавать или захватывать один электрон, то плотность дырочного заряда Q_ss на поверхностных уровнях дается соотношением (здесь предполагается, что поверхностные уровни являются донорными)

(1.145)

где N_ss - полное число донорных уровней на единице площади поверхности, - энергия поверхностного уровня при потенциале плоских зон. При этом энергия поверхностного уровня может быть определена как

(1.146)

Концентрацию поверхностных уровней можно определить на основе результатов изучения зависимости дифференциальной емкости от потенциала полупроводникового электрода. Аналитическое выражение этой зависимости имеет вид

(1.147)

где

(1.148)

а Y определяется уравнением (1.136).

Согласно (1.147), зависимости С_ss(Y) и lgC_ss(Y) имеют максимум при

(1.149)

При этом

(1.150)

Определив N_ss, можно по уравнению (1.147) оценить влияние заряда на поверхностных состояниях на распределение электрического поля границы раздела полупроводник – электролит. При этом необходимо учитывать, что емкость границы раздела представляет собой емкость эквивалентной схемы, состоящей из емкостей электролита С_el, слоя Гельгольца C_H и полупроводникового электрода. Так как заряд полупроводниковой обкладки равен сумме Q_ss+Q_sc, то дифференциальная емкость этой обкладки равна сумме емкостей С_ss+C_sc.

Все отмеченное выше демонстрирует тесную связь между физическими и физико-химическими свойствами всех составляющих компонентов границы раздела полупроводник - электролит. Для того чтобы количественно оценить эту взаимосвязь, необходимо привести энергетические параметры указанных свойств к единой шкале.

 

1.10. Энергетические характеристики ячейки

с полупроводниковым электродом

 

Качественное и количественное рассмотрение термодинамического и кинетического поведения полупроводниковых электродов принято проводить с помощью энергетической диаграммы, на которой откладывают, наряду с энергией энергетических зон полупроводника, также уровни электрохимических потенциалов. В полупроводнике это - уровень Ферми E_F, в растворе это - уровень, характеризующий электрохимический потенциал электродной реакции

(1.151)

где - равновесный потенциал соответствующей реакции, а значение константы const зависит от выбранного начала отсчета.

В физике полупроводников за начало отсчета энергии принимают энергию свободного электрона в вакууме. Поэтому, определив const в уравнении (1.151) по “физической” шкале, можно связать электрохимические и физические шкалы энергий.

Свободная энергия переноса электрона из вакуума на уровень электрохимического потенциала электрода, находящегося в равновесии с раствором, определяется как

, (1.152)

где w_mv - работа выхода электрона из электрода в вакуум, y_ms - вольта-потенциал между электродом и раствором. Используя, например, для ртутного электрода значения w=4,48 эВ и y_ms=-0,26 В при потенциале нулевого заряда (который составляет -0,19 В относительно водородного электрода), можно сопоставить “водородную” электрохимическую шкалу с физической шкалой энергий. Для водородного электрода, на котором реализуется реакция

, (1.153)

энергия переноса электрона составляет

(эВ) (1.154)

Следовательно, уровень электрохимического потенциала нормального водородного электрода лежит на 4,4 эВ ниже уровня электрона в вакууме. При этом следует обратить внимание на то, что значение энергии Ферми в растворе и равновесный электродный потенциал имеют противоположные знаки.

Для количественного расчета энергетической диаграммы контакта полупроводник - электролит традиционно применяют две основные методики. В основе обеих методик лежит определение потенциала плоских зон, при котором границы энергетических зон полупроводника в контакте с раствором имеют то же положение, что и в глубине полупроводника.

В первой методике изучают зависимость дифференциальной емкости полупроводника от приложенного потенциала. При этом, если в координатах C^-2 - j получаются прямые линии, то можно заключить, что скачок потенциала в слое Гельмгольца не зависит от условий поляризации, то есть изменение емкости связано с изменением свойств ОПЗ в полупроводнике. Экстраполяция указанной зависимости на С^-2=0 дает с точностью до 60 мВ потенциал плоских зон.

Другим способом определения потенциала плоских зон является измерение изменения электродного потенциала при генерации неравновесных носителей в ОПЗ. Это можно осуществить посредством фотоактивации поверхности полупроводника или за счет инжекции соответствующих носителей через p-n-переход, расположенный вблизи поверхности.

В зависимости от химической природы полупроводника потенциал плоских зон может оказаться функцией состава электролита. Так для оксидных полупроводников (TiO₂, ZnO и др.), а также для полупроводников, поверхность которых в водном растворе окислена (Ge, Si, GaAs и др.), потенциал плоских зон является линейной функцией рН. Это связано с изменением скачка потенциала в слое Гельмгольца, обусловленное условиями равновесия, устанавливающимся между раствором и электродом. Так, находящиеся на окисленной поверхности германия гидроксильные группы диссоциируют в водных щелочных растворах по уравнению

(1.155)

Это приводит к возникновению в слое Гельмгольца дополнительного скачка потенциала. Изменение рН приводит к смещению химического равновесия, при этом изменяется концентрация заряженных поверхностных групп и обусловленный ими скачок потенциала. В простейшем случае

(1.156)

Амфотерный характер поверхностных оксидов большинства полупроводников приводит к изменению механизма диссоциации. Так в кислом растворе реализуется основной механизм поверхностной пассивации германия по реакции

(1.157)

Следует отметить, что переход от “оксидного” к “гидридному” типу поверхности сопровождается для германия сдвигом потенциала плоских зон на 0,6 В в сторону отрицательных значений.

Для некоторых других материалов, например CdS, потенциал плоских зон в большей степени зависит от концентрации ионов серы, чем от величины рН. Это обусловлено тем, что в водном растворе на поверхности полупроводника устанавливается равновесие типа

(1.158)

или

(1.159)

Однако, несмотря на экспериментальный факт независимости потенциала плоских зон CdS от рН, говорить о независимости условий равновесия от рН в данном случае нельзя, т.к. от кислотности зависит равновесие в системе H₂S-HS^--S^2-. Кроме того, от стехиометрии поверхности зависят электронные свойства электрода и полупроводникового соединения. Поэтому обогащение металлом или металлоидом поверхности электрода существенно изменяет энергетические характеристики границы раздела.

 

1.11 Методика построения энергетической диаграммы

полупроводник - электролит

 

Построение энергетической диаграммы на основе экспериментальных данных проводит в следующей последовательности. Сначала определяют потенциал плоских зон или, что, то же самое, определяют положение уровня Ферми полупроводника относительно выбранного электрода сравнения в шкале электродных потенциалов. Далее с помощью формулы (1.154) определяют положение E_F в физической шкале энергий. Затем по известному значению концентрации основных носителей определяется положение уровня Ферми относительно границы зоны основных носителей. Для этого применяют формулы:

1. Для собственного полупроводника

(1.160)

2. Для полупроводника n-типа

(1.161)

3. Для полупроводника р-типа

(1.162)

где N_c и N_v - эффективная плотность состояний в зоне проводимости и валентной зоне соответственно, n₀ и p₀ - равновесные концентрации электронов и дырок соответственно.

Эффективная плотность состояний определяется следующими соотношениями

и (1.163)

где m_n и m_p - эффективные массы соответственно электронов на дне зоны проводимости и дырок под потолком валентной зоны.

Зная ширину запрещенной зоны полупроводника, нетрудно определить положение границы зоны неосновных носителей.

 

1.12 Кинетика электродных реакций на полупроводниковых

электродах

 

Рассмотрим полупроводниковый электрод, на котором протекает окислительно-восстановительная электрохимическая реакция:

Ox + ne «Red. (1.164)

В отличие от металлов в электродном процессе на полупроводниковом электроде могут принимать участие электроны как из зоны проводимости, так и из валентной зоны. В рассматриваемой обратимой реакции участвуют четыре различных электронных перехода, представленных на рис.1.12. Переходы электронов из полупроводника в электролит и дырок из электролита в полупроводник дают вклад в катодный ток, а соответствующие обратные переходы - в анодный. Таким образом, полный ток складывается из четырех токов, а рассматриваемая реакция из двух парциальных реакций, которые можно представить в виде:

Ox + ne^- «Red, (1.165)

Ox «Red + np⁺ (1.166)

Рис.1.12. Электронные и дырочные токи на границе раздела полупроводника с электролитом, содержащим окислительно-восстановительную систему.

 

В состоянии термодинамического равновесия ток (имеется в виду плотность тока), идущий через границу за счет переноса электронов с реагента в растворе на электрод, может быть записан в виде

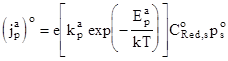(1.167)

где C^o_Red,s - равновесная концентрация частиц Red в растворе вблизи поверхности (очевидно в слое Гельмгольца), p^o_s - равновесная концентрация дырок в валентной зоне вблизи поверхности полупроводника, т.е. свободных мест для электронов, переходящих с реагента на электрод по реакции (1.166).

В отсутствие вырождения величина p^o_s может быть записана в виде

, (1.168)

где j^o_sc - равновесный потенциал в полупроводнике.

Аналогичным образом равновесный ток электронов для реакции (1.166) дается соотношением

(1.169)

где C^o_Ox,s - равновесная приповерхностная концентрация Ox, n_v - приповерхностная концентрация электронов в валентной зоне, которую можно считать постоянной и не зависящей от потенциала.

Энергия активации , входящая в уравнение (1.167), есть функция падения потенциала в той области, где происходит разряд, т.е. в слое Гельмгольца. Таким образом, зависимость энергии активации от перенапряжения можно представить в виде

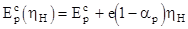, (1.170)

Согласно (1.170) величина энергетического барьера изменяется линейно вместе с изменением разности энергий между начальным и конечным состояниями.

Принимая во внимание условие равновесия

(1.171),

ток, связанный с электрохимической реакцией, идущей через валентную зону, можно выразить через равновесный ток обмена в виде

(1.172)

С помощью аналогичных выкладок получается, что ток, связанный с электрохимической реакцией, идущей через зону проводимости, равен

(1.173)

При этом ток обмена электродной реакции через зону проводимости равен

(1.174)

где p_c - приповерхностная концентрация незанятых электронами уровней в зоне проводимости, p_c»N_c; величина 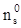зависит от равновесного значения и в отсутствие вырождения определяется выражением

(1.175)

Соотношения (1.173) и (1.174) описывают электронные токи через валентную зону и зону проводимости при протекании на границе электрохимической реакции. Полный электрический ток, идущий через единицу площади поверхности раздела, равен

(1.176)

Достаточно часто токи обмена для различных зон сильно различаются, и потому определяющая роль принадлежит какому-либо одному слагаемому в уравнении (1.176).

Если токи электродных реакций достаточно малы, так что величины j_p и j_n меньше предельных токов по реагентам Red и Ox, то можно не учитывать концентрационную поляризацию. Другими словами, протекание тока не искажает в этих условиях распределение концентрации C_Red и C_Ox, т.е.

(1.177)

где C_Red и C_Ox - концентрации компонентов Red и Ox в глубине раствора. При выполнении этого условия уравнения (1.172) и (1.173) принимают вид

(1.178)

 

(1.179)

Если основное падение потенциала происходит в слое Гельмгольца (поверхностное вырождение или высокая концентрация поверхностных состояний), то h=h_H. При этом поверхностные концентрации носителей заряда равны их равновесным значениям, и, например, для тока реакции через зону проводимости, получается выражение

(1.180)

Аналогия между уравнениями (1.180) для полупроводника и (1.99) для металла подтверждает справедливость термина “металлизация” поверхности полупроводника при высокой концентрации электронов в приповерхностной области.

Если все падение потенциала происходит в полупроводнике, то перенапряжение в слое Гельмгольца равно нулю. Тогда, учитывая распределение Больцмана для электронов, получается следующее выражение для плотности электронного тока

(1.181)

При высоких перенапряжениях, когда e|h|/kT>>1, получается выражение, аналогичное зависимости Тафеля, выведенное для металлического электрода

(1.182)

Зависимость Тафеля для полупроводникового электрода может также выполняться и в случае, когда перенапряжение в слое Гельмгольца изменяется пропорционально приложенному потенциалу при условии a_n=0. Однако физический смысл уравнения (1.181) оказывается отличным от случая “металлизации”.

 

1.13 Электрохимическое разложение и пассивность полупроводников

 

Процесс разложения полупроводника можно представить следующей реакцией

(1.183)

где M_s - материал твердого электрода, L_l - комплексообразующий компонент раствора, ML_l - растворимый продукт реакции.

Эта реакция может быть охарактеризована определенным электрохимическим потенциалом, который мы назовем электрохимическим потенциалом разложения полупроводника и обозначим как E_Dec,p. Для определения этого потенциала удобно пользоваться диаграммами Пурбе. Возможность протекания той или иной электрохимической реакции определяется следующими соотношениями между потенциалами или уровнями Ферми

или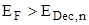

для катодной реакции с участием электронов зоны проводимости и

или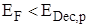

для анодной реакции с участием дырок из валентной зоны.

Для того чтобы в каждой конкретной системе определить, подвержен ли полупроводник электрохимическому разложению, обратимся к энергетической зонной диаграмме, на которой отложим уровни электрохимического потенциала для реакций разложения. Как схематически изображено на рис.1.13, здесь возможны различные ситуации. Полупроводник устойчив к катодному разложению, если уровень электрохимического потенциала соответствующей реакции попадает в зону проводимости, и к анодному, если он попадает в валентную зону. В обоих случаях, если изменение потенциала сосредоточено целиком в полупроводнике (“закрепление зон на поверхности”), этот уровень оказывается “недостижимым” для уровня Ферми полупроводника. Полупроводник абсолютно устойчив, если уровни обеих реакций разложения лежат за пределами запрещенной зоны (рис.1.13, a). Чаще встречаются случаи, когда полупроводник устойчив только по отношению к какому-нибудь одному типу разложения: к катодному (рис.1.13, б) или анодному (рис. 1.13,в). Наконец, если оба уровня F_Dec,n и F_Dec,p лежат в запрещенной зоне (рис.1.13, г), то и при катодной, и при анодной поляризации полупроводник может подвергаться разложению.

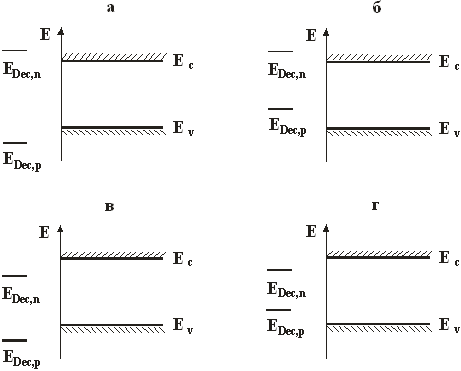
Рис. 1.13. Схема, иллюстрирующая термодинамическую устойчивост