Операционное исчисление.

• 20.1. Определение функции-оригинала и её изображения по Лапласу.
• 20.1.1. Определение функции-оригинала.
  
• 20.1.2. Определение изображения по Лапласу.
  
• 20.1.3. Изображения простейших функций.
  
• 20.2. Свойства преобразования Лапласа.
• 20.2.1. Линейность преобразования Лапласа.
• 20.2.2. Теорема подобия.
  
• 20.2.3. Теорема смещения.
  
• 20.2.4. Теорема запаздывания.
  
• 20.2.5. Интегрирование оригинала.
  
• 20.2.6. Дифференцирование оригинала.
  
• 20.2.7. Интегрирование изображения.
  
• 20.2.8. Дифференцирование изображения.
  
• 20.2.9. Изображение свёртки функций. Теорема Бореля. Интегралы Дюамеля.
• 20.3. Таблица стандартных изображений.
  20.4. Обращение преобразования Лапласа.
• 20.4.1. Формула Римана-Меллина.
  
• 20.4.2. Элементарный метод нахождения оригинала.
• 20.4.3. Первая теорема разложения.
• 20.4.4. Вторая теорема разложения.
• 20.5. Приложения операционного исчисления к решению линейных дифференциальных уравнений и их систем.
• 20.5.1. Задача Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами.
• 20.5.2. Общее решение дифференциального уравнения с постоянными коэффициентами.
• 20.5.3. Краевая задача для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами.
• 20.5.4. Уравнения с импульсной и составной правой частью.
• 20.5.5. Формулы Дюамеля.
• 20.5.6. Решение систем линейных уравнений.

Мы будем изучать операционное исчисление как один из методов решения линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений. Каких-либо решающих преимуществ этот метод перед другими не имеет; в то же время его простота сделала его основным инструментом при решении задачи Коши в целом ряде прикладных наук (механике, радиотехнике, электротехнике и т.д.).
Идея операционного исчисления состоит в следующем. Пространство функций, удовлетворяющих некоторым достаточно общим условиям (пространство функций-оригиналов) взаимно однозначно отображается в другое пространство функций (пространство функций-изображений) так, что операциям дифференцирования и интегрирования в пространстве функций-оригиналов соответствуют более простые операции (конкретно - операции умножения и деления) в пространстве функций-изображений. В результате дифференциальное уравнение в пространстве функций-оригиналов преобразуется в линейное алгебраическое уравнение в пространстве функций-изображений, решение которого находится без проблем. Последнее действие - восстановление решения уравнения по его изображению.
Таким образом, мы должны изучить следующие вопросы:
1. Какие функции могут быть функциями-оригиналами и каковы свойства функций-изображений;
2. Каковы правила перевода оригиналов в изображения и обратно;
3. Какие изображения имеют основные элементарные функции (таблица стандартных изображений).

20.1. Определение функции-оригинала и её изображения по Лапласу. 20.1.1.

Определение. Будем называть функцией-оригиналом действительнозначную или комплекснозначную функцию f (t) действительной переменной t, удовлетворяющую условиям:
1. f (t) = 0 при t < 0;
2. Существуют такие постоянные M > 0 и σ₀ ≥ 0, что | f (t) | ≤ M · e ^σ₀ ^t;
3. На любом отрезке [ a, b ] (0 ≤ a < b < ∞) функция удовлетворяет условиям Дирихле (т.е. непрерывна или имеет конечное число устранимых разрывов и разрывов первого рода; монотонна или имеет конечное число экстремумов).
Смысл этих условий такой.
1. Так как одно из основных приложений операционного исчисления - решение задач с начальными условиями (задач Коши), то поведение функций до начального момента t = 0 несущественно;
2. Параметр σ₀ во втором условии принято называть показателем роста функции f (t). Само второе условие означает, что скорость роста функции-оригинала не может быть больше экспоненциальной. В совокупности с третьим условием это обеспечивает существование и определенные полезные свойства функции-изображения и не является обременительным.
Приведём примеры функций-оригиналов. Для всех этих функций первое и третье свойства выполняются очевидно, поэтому будем проверять только второе свойство.
1. Единичная функция Хевисайда. Так называется функция, Очевидно, это - функция-оригинал (η (t) < e ^t).
2. . Заметим, что с помощью единичной функции Хевисайда η (t) определение этой функции можно записать короче: f (t) = t ^α · η (t) (α ≥ 0), так как функция η (t) в качестве множителя обнуляет любую другую функцию при t < 0. Дальше мы будем писать просто f (t) = t ^α , f (t) = e ^{α t} , f (t) = sin t, f (t) = cos t и т.д., имея в виду, что все функции начинаются в момент t = 0, и при t < 0 тождественно равны нулю.
Для функции f (t) = t ^α получаем: t < e ^t при t ≥ 0, поэтому t ^α < e ^{α t} .
3. f (t) = sin t. | sin t | ≤ 1 = 1· e ^{0· t} и т.д.
Примеры функций, не являющихся оригиналами:
1. Эта функция имеет разрыв второго рода в точке t = 1.
2. Функция имеет бесконечное число экстремумов на отрезке [0,1].
3. Не существует таких констант M и σ₀, что | f (t) | ≤ M · e ^σ₀ ^t.

20.1.2. Определение. Изображением по Лапласу функции-оригинала f (t) (или преобразованием Лапласа функции f (t)) называется функция комплексной переменной p, определяемая равенством
.
Интеграл в правой части этого определения сходится абсолютно в любой точке p, удовлетворяющей неравенству Re p ≥ σ₁, где σ₁ - произвольной число, такое, что σ₁ > σ₀. Действительно, (так как | e ^{− i Im p · t} | = | cos(Im p · t) − i sin(Im p · t)| = 1) = M | e ^{−Re p · t} |· e ^·σ₀ ^t = M e ^{−(Re p − σ}₀^{) t} ≤ M e ^−(σ₁ ^{− σ}₀^{) t} , а интеграл сходится. Таким образом, мы доказали, что изображение F (p) определено в любой точке p, такой что Re p > σ₀, т.е. в полуплоскости справа от прямой Re p = σ₀. Как следствие, показатель скорости роста оригинала число σ₀ часто называют абсциссой сходимости.
Заметим, что мы доказали также, что : так как | e ^{− pt} · f (t)| ≤ M e ^{−(Re p − σ}₀^{) t} , то . Кроме того, в оценке | e ^{− pt} · f (t)| ≤ M e ^−(σ₁ ^{− σ}₀^{) t} мы мажорировали модуль подынтегральной функции функцией, не зависящей от p, интеграл от которой сходится. Как и в теории функциональных рядов, этого достаточно, чтобы сходимость интеграла была равномерной по переменной p, поэтому функцию F (p) можно дифференцировать и интегрировать по этой переменной.
20.1.3. Изображения простейших функций.
20.1.3.1. Единичная функция Хевисайда Её изображение: , так как . Соответствие между функцией-оригиналом и изображением обозначается по-разному: знаком равенства с точками, стрелками с точками и т.д.; мы будем применять обозначения f (t) F (p) и f (t) F (p), наиболее подходящие из имеющихся в Word’е. Итак, доказано: .
20.1.3.2. f (t) = e ^{α t} .
.
20.1.3.3. f (t) = sin ω t. (мы с помощью двукратного интегрирования по частям сводим интеграл к самому себе) . Для F (p) получено уравнение . Итак, .
20.1.3.4. f (t) = cos ω t. Аналогично предыдущему доказывается, что .
20.1.3.5. Степенная функция f (t) = t ⁿ. При n = 1 находим , так как . Итак, . Аналогично можно доказать, что , , и вообще при целом n . Дальше мы получим более простой вывод этих формул с помощью теоремы о дифференцировании изображения.

20.2. Свойства преобразования Лапласа.

20.2.1. Линейность преобразования Лапласа. Если f (t), g (t) - функции-оригиналы, имеющие изображения F (p), G (p), то их линейная комбинация α f (t) + β g (t) (α = cost, β = const)- тоже функция-оригинал, и α f (t) + β g (t) α F (p) + β G (p).
Это свойство непосредственно следует из свойства линейности несобственного определённого интеграла. С его помощью можно более просто вывести изображения функций sin t, cos t, исходя из изображения : ; . Далее, ; .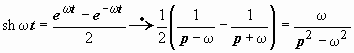
20.2.2. Теорема подобия. Если f (t) - функция-оригинал и f (t) F (p), то для любого λ

> 0 .
Док-во. .
Иллюстрации применения этого свойства: если 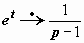, то ; если , то и т.д.
20.2.3. Теорема смещения. Если f (t) F (p), то e ^{α t} f (t) F (p − α),. Здесь α - произвольное комплексное число.
Док-во. .
Иллюстрации применения этого свойства: если , то ; если , то и т.д.
20.2.4. Теорема запаздывания. Если f (t) F (p) (т.е. f (t) · η (t) F (p)), то f (t − t ₀) · η (t − t ₀) e ^{− t} ₀ ^{· p} · F (p) для любого числа t ₀ ≥ 0.
Док-во. .
Теорема запаздывания применяется для изображения функций импульсных, составных, периодических. Рассмотрим этот вопрос подробнее.
20.2.4.1. Импульсные функции.
Единичный импульс: С помощью функции Хевисайда эта функция записывается так: . Мы знаем, что ; по теореме запаздывания

(t ₀ = 1) , поэтому .
Запаздывающий прямоугольный импульс: Здесь .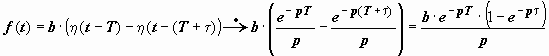
Треугольный импульс. Аналитически эта функция записывается так: Изменение функции на переходе от участка T ≤ t ≤ T + τ к участку T + τ ≤ t ≤ T + 2τ равно ; при переходе к участку t > 2τ изменение функции равно , поэтому можно переписать , и, так как , , то .
Синусоидальный импульс. Здесь , поэтому .
20.2.4.2. Составные функции. Пусть f (t) задаётся разными выражениями на различных участках области определения:

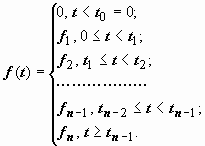. С помощью функции Хевисайда f (t) записывается так: , и теорема запаздывания позволяет получить изображение этой функции.
20.2.4.3. Периодические функции. Пусть f (t)- периодическая при t > 0 функция с основным периодом, равным T. Обозначим f ₁(t) функцию, описывающую первый период функции f (t):
. Теперь (каждое слагаемое описывает соответствующий период). Пусть - изображение функции f ₁(t). Тогда
.
Найдём в качестве примера изображение функции { t } - дробной части числа t. Эта функция определяется так: { t } = t – n при n ≤ t < n + 1, n - целое число. Для неё , или f ₁(t) = t · [ η (t) − η (t − 1)] = t · η (t) − (t − 1) η (t − 1) − 1 · η (t − 1), поэтому , и .
20.2.5. Интегрирование оригинала. Если f (t) - функция-оригинал, и f (t) F (p), то - тоже функция-оригинал, и .
Док-во. (это повторный интеграл, вычисляемый по области {0 ≤ t < +∞, 0 ≤ τ ≤ t }; меняем порядок интегрирования, это можно сделать, так как несобственный двойной интеграл сходится абсолютно)

.
20.2.6. Дифференцирование оригинала. Если функция-оригинал f (t) имеет производную f ′(t), тоже являющуюся оригиналом, и f (t) F (p), то f ′(t) p F (p) − f (+0).
Док-во. Мы пишем здесь f (+0), а не f (0), так как оригинал может иметь разрыв (первого рода) в точке t = 0.
Формула дифференцирования оригинала может применяться неоднократно. Если функция-оригинал f (t) имеет производные f ′(t), f ″(t), f ′″(t), f ⁽⁴⁾(t), …, f ⁽ⁿ⁾(t), и все они тоже являются оригиналами, имеющими изображения F ₁(p), F ₂(p), F ₃(p), …, F_n (p), то, как только что доказано, f ′(t) F ₁(p) = p F (p) − f (+0). Тогда f ″(t) F ₂(p) = p F ₁(p) − f ′(+0) = p ² F (p) − p f (+0) − f ′(+0), f ″′(t) F ₃(p) = p F ₂(p) − f ″(+0) = p ³ F (p) − p ² f (+0) − p f ′(+0) − f ″(+0), …, f ⁽ⁿ⁾(t) F_n (p) = p ⁿF (p) − p ^{n − 1} f (+0) − p ^{n − 2} f ′(+0) − p ^{n − 3} f ″(+0) − … − p f ^{(n − 2)}(+0) − f ^{(n − 1)}(+0).
20.2.7. Интегрирование изображения. Пусть f (t) - функция-оригинал, f (t) F (p), и функция ограничена в окрестности точки t = 0. Тогда тоже является оригиналом и .
Док-во. Проинтегрируем равенство по переменной q = ρ + i η по горизонтальному лучу, проведённому из точки p = ξ + i η, где ξ ≤ ρ = Re q < +∞: .
Иллюстрации применения теорем об интегрировании изображения и оригинала:
1. Найти изображение интегрального синуса .
Решение: (по теореме 20.2.7)
(по теореме 20.2.5) .
2. Найти изображение функции .
Решение. .
20.2.8. Дифференцирование изображения. Если f (t) - функция-оригинал, и f (t) F (p), то − t f (t) F ′(p).
Док-во. . Дифференцируя это соотношение по параметру р, получаем .
Иллюстрации этого свойства. С его помощью просто получаются изображения степенных функций: 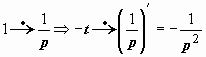, или ; , или , , или ; , или , и вообще .
Другие иллюстрации: , …, .

и т.д.
20.2.9. Изображение свёртки функций. Теорема Бореля. Интегралы Дюамеля.
20.2.9.1. Свёртка функций и её свойства.
Определение. Сверткой функций f ₁(t) и f ₂(t) называется функция .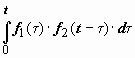
Свёртка обозначается символом f ₁ * f ₂: . Если f ₁(t) и f ₂(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f ₁(t) и f ₂(t) не больше, чем на 1. Действительно, пусть , , , тогда , так как t < e ^t.
Свёртка функций коммутативна: f (t) * g (t) = g (t) * f (t), в этом легко убедиться, заменив в интеграле 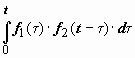переменную τ на τ ₁ = t − τ.
Можно показать, что свёртка обладает свойством ассоциативности, т.е. что (f ₁ * f ₂) * f ₃ = f ₁ * (f ₂ * f ₃).
20.2.9.2. Теорема Бореля (теорема об умножении изображений). Изображение свёртки двух оригиналов равно произведению изображений свёртываемых оригиналов.
Док-во. (меняем порядок интегрирования)= .
С помощью этой теоремы легко находить оригиналы для изображений вида F ₁(p)· F ₂(p).
Примеры. Найти оригиналы, если
1. . Здесь , , поэтому .
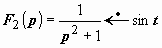2. . Здесь , , поэтому .
3. . Здесь , поэтому .
20.2.9.3. Интегралы Дюамеля. Запишем с помощью теоремы Бореля оригиналы для выражения вида pF (p) G (p), где F (p) и G (p) - изображения функций f (t) и g (t). С одной стороны, (так как, по теореме 20.2.8, ); с другой стороны, .
В развёрнутом виде
,
.
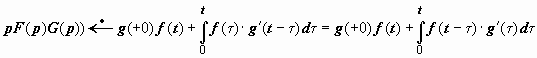Каждая из этих формул называется интегралом Дюамеля.

20.3. Таблица стандартных изображений.

Сведём в таблицу полученные ранее изображения элементарных функций.

	f (t)	F (p)			f (t)	F (p)
1.				9.	e α t · sin β t
2.	t n			10.	e α t · cos β t
3.	e α t			11.	e α t · sh β t
4.	e α t · t n			12.	e α t · ch β t
5.	sin β t			13.	t · sin β t
6.	cos β t			14.	t · cos β t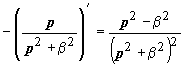
7.	sh β t			15.	t · sh β t
8.	ch β t			16.	t · ch β t

20.4. Обращение преобразования Лапласа.

20.4.1. Формула Римана-Меллина. Если функция F (p) - изображение функции-оригинала f (t), то f (t) может быть найдена по формуле
.
Это равенство имеет место в каждой точке, в которой f (t) непрерывна. В точках разрыва функции f (t) значение правой части равно . Интеграл в правой части формулы называют интегралом Меллина; интегрирование может вестись по любой вертикальной прямой p = σ + i ω, σ = const > σ₀, − ∞ < ω < ∞, и интеграл понимается в смысле главного значения: .
Вычисление оригинала по формуле Римана-Меллина довольно трудоёмко, поэтому на практике при решении задач применяют другие методы, которые рассматриваются ниже.
20.4.2. Элементарный метод нахождения оригинала. Этот метод основан на непосредственном применении таблицы стандартных изображений 20.3 и свойств преобразования Лапласа.
Примеры. 1. . Представляя изображение в виде и сравнивая эти выражения с формулами 9, 10 таблицы, находим оригинал .
2. . Наличие степеней переменной р в знаменателе позволяет применить теорему 20.2.5 об интегрировании оригинала: , , .
Можно решить этот пример с помощью свёртки: , . Однако проще всего представить F (p) в виде суммы простых дробей .
20.4.3. Первая теорема разложения. Если точка p = ∞ является нулём функции F (p), F (p) аналитична в окрестности этой точки и разложение функции по степеням р в окрестности точки p = ∞ имеет вид , то функция F (p) есть изображение

функции .
Это выражение получается в результате почленного перехода к оригиналам в ряде : так как , то , и .
Примеры. 1. . Условия теоремы выполнены. Лорановское разложение функции F (p) в окрестности точки p = ∞: .
2. . Здесь .
20.4.4. Вторая теорема разложения. Пусть функция F (p) комплексной переменной р аналитична во всей плоскости, за исключением конечного числа изолированных особых точек p ₁, p ₂, p ₃, …, p_n, расположенных в полуплоскости Re p < σ₀. Если , и F (p) абсолютно интегрируема вдоль любой вертикальной прямой Re p = σ, σ > σ₀, то F (p) является изображением, и .
Док-во. Сведём интеграл в формуле Римана-Меллина к интегралу по замкнутому контуру. Контур Γ составим из отрезка AB прямой Re p = σ, σ > σ₀, и дуги C_R окружности | p | = R, расположенной слева от отрезка и содержащей внутри себя все особые точки функции F (p). По основной теореме о вычетах . , поэтому . Устремим R → +∞. По лемме Жордана ; а для второго интеграла получаем , поэтому в пределе .
Применим эту теорему для обращения изображения . Функция F (p) · e ^pt имеет три особых точки: p = 0 (полюс второго порядка) и (простые полюсы), поэтому . Находим вычеты: ;