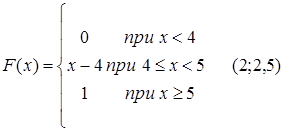41-60. Задан закон распределения дискретной случайной величины X.
Найти: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение; 4) построить многоугольник распределения и показать на нем математическое ожидание и среднее квадратическое отклонение; 5) интегральную функцию распределения F(х);
6) построить график функции распределения F(х).
| X | |||||
| p | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 |
41.
| X | |||||
| p | 0,3 | 0,15 | 0,25 | 0,2 | 0,1 |
42.
| X | |||||
| p | 0,5 | 0,15 | 0,2 | 0,05 | 0,1 |
43.
| X | |||||
| p | 0,1 | 0,25 | 0,3 | 0,2 | 0,15 |
44.
| X | |||||
| p | 0,25 | 0,2 | 0,4 | 0,1 | 0,05 |
45.
| X | |||||
| p | 0,4 | 0,2 | 0,15 | 0,2 | 0,05 |
46.
| X | |||||
| p | 0,2 | 0,1 | 0,4 | 0,2 | 0,1 |
47.
| X | |||||
| p | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
48.
| X | |||||
| p | 0,1 | 0,4 | 0,3 | 0,15 | 0,05 |
49.
| X | |||||
| p | 0,1 | 0,2 | 0,25 | 0,05 | 0,4 |
50.
| X | |||||
| p | 0,1 | 0,35 | 0,3 | 0,05 | 0,2 |
51.
| X | |||||
| p | 0,1 | 0,35 | 0,4 | 0,05 | 0,1 |
52.
| X | |||||
| p | 0,1 | 0,1 | 0,3 | 0,3 | 0,2 |
53.
| X | |||||
| p | 0,2 | 0,2 | 0,3 | 0,2 | 0,1 |
54.
| X | |||||
| p | 0,05 | 0,2 | 0,4 | 0,2 | 0,15 |
55.
| X | -5 | -1 | |||
| p | 0,2 | 0,4 | 0,2 | 0,1 | 0,1 |
56.
| X | |||||
| p | 0,25 | 0,3 | 0,3 | 0,1 | 0,05 |
57.
| X | -10 | ||||
| p | 0,05 | 0,2 | 0,3 | 0,3 | 0,15 |
58.
| X | |||||
| p | 0,05 | 0,1 | 0,6 | 0,1 | 0,15 |
59.
| X | |||||
| p | 0,2 | 0,1 | 0,3 | 0,3 | 0,1 |
60.
Решение типовой задачи.
Задача 7. Задан закон распределения дискретной случайной величины:
| xi | -1 | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,2 | 0,1 |
Найти: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение; 4) построить многоугольник распределения и показать на чертеже математическое ожидание и среднее квадратическое отклонение; 5) интегральную функцию распределения F(х); 6) построить график функции распределения F(х).
Решение.
1) Математическое ожидание дискретной случайной величины вычисляется по формуле:
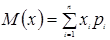
2) Дисперсия дискретной случайной величины вычисляется по формуле:
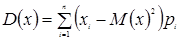
и по упрощенной формуле 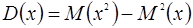 , где
, где 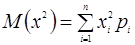 .
.
Расчёт числовых характеристик по этим формулам будет производиться с помощью таблицы

| 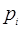
| 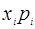
| 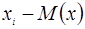
| 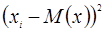
| 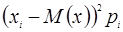
| 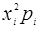
|
| -1 | 0,2 | -0,2 | -13,3 | 176,89 | 35,378 | 0,2 |
| 0,1 | 0,6 | -6,3 | 39,69 | 3,969 | 3,6 | |
| 0,4 | 5,2 | 0,7 | 0,49 | 0,196 | 67,6 | |
| 0,2 | 4,0 | 7,7 | 59,29 | 11,858 | 80,0 | |
| 0,1 | 2,7 | 14,7 | 216,09 | 21,609 | 72,9 | |

| 12,3 | 73,010 | 114,3 |
Из таблицы имеем 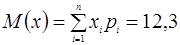 .
. 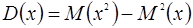 ,
, 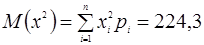 ,
, 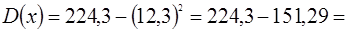
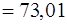 ,
, 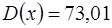 .
.
3) Среднее квадратичное отклонение:
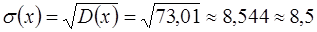 .
.
4) Делаем чертёж. По оси абсцисс откладываем в выбранном масштабе значение случайной величины, по оси ординат – соответствующие вероятности. Масштаб по осям откладываем разный. Строим точки с координатами 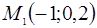 ,
, 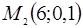 ,
, 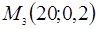 ,
, 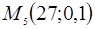 .
.
Полученные точки соединяем прямыми линиями. Получаем многоугольник распределения вероятностей заданный случайной величины.
|
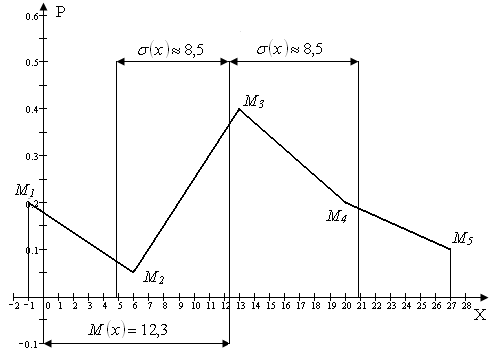
Вычисленное значение математического ожидания откладываем от начала координат по оси абсцисс 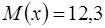 . От значения математического ожидания вправо и влево откладываем отрезки размером в одно среднее квадратичное отклонение. Чертёж представлен на рисунке 1.
. От значения математического ожидания вправо и влево откладываем отрезки размером в одно среднее квадратичное отклонение. Чертёж представлен на рисунке 1.
5) Интегральная функция распределения определяется следующим образом:
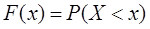
Разобьем числовую прямую на интервалы:
(-¥;-1); [-1;6); [6;13); [13;20); [20;27); [27;+¥)
 -¥ -1 6 13 20 27 +¥
-¥ -1 6 13 20 27 +¥
Найдем значения функции F(x) на этих интервалах:
1. при х 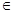 (-¥;-1) Þ F(x)=P(X< x)=0, т.к. в этом промежутке случайная величина Х не принимает ни одного значения, меньшего х.
(-¥;-1) Þ F(x)=P(X< x)=0, т.к. в этом промежутке случайная величина Х не принимает ни одного значения, меньшего х.
2. при х 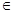 [-1;6) Þ F(x)=P(X< x)=P(X=-1)=0,2, т.к. в этом промежутке случайная величина Х принимает одно значение х 1= -1, меньше х.
[-1;6) Þ F(x)=P(X< x)=P(X=-1)=0,2, т.к. в этом промежутке случайная величина Х принимает одно значение х 1= -1, меньше х.
3. при х 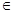 [6;13) Þ F(x)=P(X< x)=P(X= -1)+Р(Х=6)=0,2+0,1=0,3, т.к. на данном промежутке Х принимает два значения х 1= -1 или х 2= 6, меньше х.
[6;13) Þ F(x)=P(X< x)=P(X= -1)+Р(Х=6)=0,2+0,1=0,3, т.к. на данном промежутке Х принимает два значения х 1= -1 или х 2= 6, меньше х.
4. при х 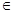 [13;20) Þ F(x)=P(X=-1)+Р(Х=6)+Р(Х=13)=0,2+0,1+0,4=0,7, т.к. левее значения Х из этого промежутка находятся значения
[13;20) Þ F(x)=P(X=-1)+Р(Х=6)+Р(Х=13)=0,2+0,1+0,4=0,7, т.к. левее значения Х из этого промежутка находятся значения
х 1= -1, х 2= 6, х 3=13.
5. при х 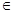 [20;27)Þ
[20;27)Þ
F(x)=P(X=-1)+Р(Х=6)+Р(Х=13)+Р(Х=20)=0,2+0,1+0,4+0,2=0,9, т.к. левее значения Х из этого промежутка находятся значения
х 1= -1, х 2= 6, х 3=13, х 4= 20
6. при х 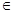 [20;+¥) Þ
[20;+¥) Þ
F(x) = P(X= -1)+Р(Х=6)+Р(Х=13)+Р(Х=20)=0,1+0,3+0,4+0,2=1
Следовательно, интегральная функция распределения будет иметь вид:
 |
0, при х 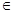 (-¥;-1)
(-¥;-1)
0,2 при х 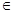 [-1;6)
[-1;6)
F(x)= 0,3 при х 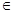 [6;13)
[6;13)
0,7 при х 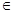 [13;20)
[13;20)
0,9 при х 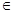 [20;27)
[20;27)
1, при х 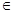 [27;+¥)
[27;+¥)
6) Строим график. По оси абсцисс откладываем значения случайной величины, а по оси ординат соответствующие значения F(x). Получим изолированные отрезки, образующие график интегральной функции для дискретной случайной величины (рисунок 2).
 | |||
 | |||
Рисунок 2.
Тема 4. Непрерывная случайная величина (задачи 61-80). Перед выполнением задач необходимо изучить вопросы 1.5 первого раздела дисциплины и разобрать решение задачи 8.
№ 61 – 80. Непрерывная случайная величина X задана функцией распределения F(х). Найти 1) плотность распределения f(х); 2)математическое ожидание; 3) дисперсию и среднее квадратичное отклонение; 4)вероятность попадания случайной величины в данный интервал 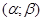 ; 5) построить графики функции распределите F (х) и плотности распределения f(х).
; 5) построить графики функции распределите F (х) и плотности распределения f(х).
61. 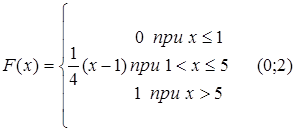
62. 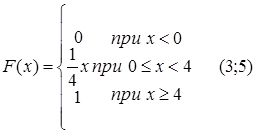
63. 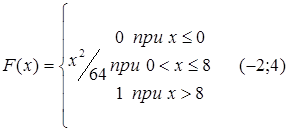 .
.
64. 
65. 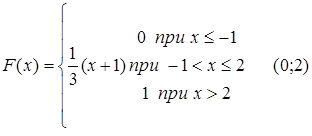
66. 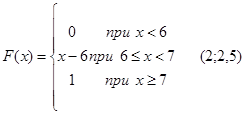
67. 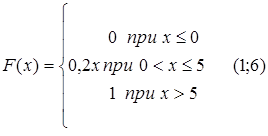
68. 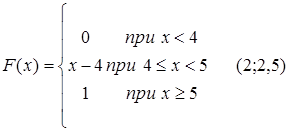
69. 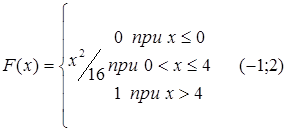
70. 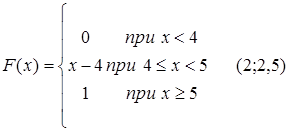
71. 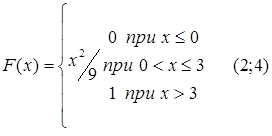
72. 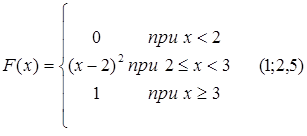
73. 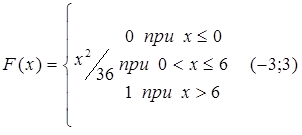
74. 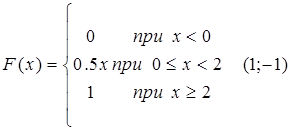
75. 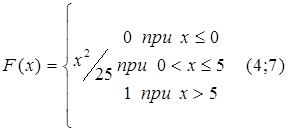
76. 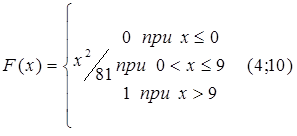
77. 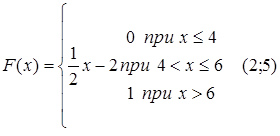
78. 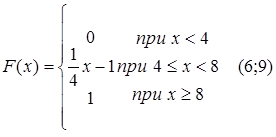
79. 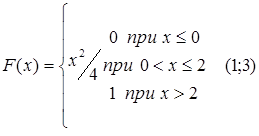
80.